1. Bubble sorting

Suppose there are 10 numbers, the first cycle, the comparison between the first number and the second number. If the first number is large, the first number and the second number exchange positions, otherwise they will not move. Then the second number and the third number exchange positions, if the second number is large, the second number and the third number exchange positions, otherwise they will not move... When comparing the ninth number with the tenth number, if the ninth number is large, the ninth number and the tenth number exchange positions, otherwise they will not move. At the end of the first cycle, the maximum number was moved to the tenth number, and the comparison was carried out 9 times.  
In the second cycle, the first number is compared with the second number. If the first number is large, the first number and the second number exchange positions, otherwise they will not move... When comparing the eighth number with the ninth number, if the eighth number is large, the eighth number and the ninth number exchange positions, otherwise they will not move. At the end of the second cycle, the second largest number was moved to the ninth number, and the comparison was conducted eight times.  
...... 
In the ninth cycle, the first number and the second number are compared. If the first number is large, the first number and the second number exchange positions, otherwise they will not move. At the end of the ninth cycle, the next to last number was moved to the second number, and the comparison was carried out once.  
General principle: find the maximum number in each round of comparison.

Code:

public class BubbleSort {
    public static void main(String[] args) {
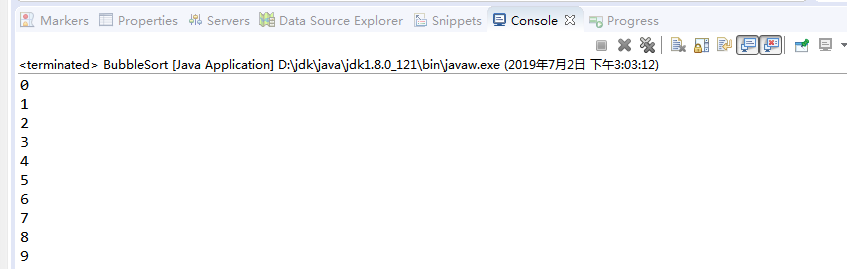
        int a[] = { 2, 3, 6, 4, 0, 1, 7, 8, 5, 9 };
        bubbleSort(a);
    }

    public static void toString(int[] a) {
        for (int i = 0; i < a.length; i++) {
            System.out.println(a[i]);
        }
    }

    private static void bubbleSort(int[] a) {
        int length = a.length;
        int temp = 0;
        for (int j = 0; j < a.length - 1; j++) {
            for (int i = 0; i < a.length - 1 - j; i++) {
                if (a[i] > a[i + 1]) {
                    // change
                    temp = a[i + 1];
                    a[i + 1] = a[i];
                    a[i] = temp;
                }
            }
        }
        toString(a);
    }
}

Result:

 

2. Quick sorting

Fast sorting is the upgrade of bubbling sorting that we learned before. They are all exchange sort, and they all use continuous comparison and movement to achieve sorting. Fast sorting is a very efficient sorting algorithm. Its implementation increases the distance between comparison and movement of records, moves records with larger keywords from the front to the back, and records with smaller keywords from the back to the front, thus reducing the total number of comparisons and movements. At the same time, the idea of "divide and rule" is adopted to divide the large into small ones and the small into smaller ones. The principle is as follows: for a given set of records, select a reference element, usually select the first element or the last element, and divide the sequence to be arranged into two parts through a scan. One part is smaller than the reference element, and the other part is greater than or equal to the reference element. At this time, the reference element The element is in the correct position after it is sorted, and then the two parts are sorted recursively by the same method until all the records in the sequence are in order.

You can see the dynamic chart to feel it:

 

 

Code:

public class QuickSort {
    public static void quickSort(int[] arr,int low,int high){
        int i,j,temp,t;
        if(low>high){
            return;
        }
        i=low;
        j=high;
        //temp is the reference level
        temp = arr[low];
 
        while (i<j) {
            //First look at the right side, then decrease to the left
            while (temp<=arr[j]&&i<j) {
                j--;
            }
            //Look at the left side again, increasing in order to the right
            while (temp>=arr[i]&&i<j) {
                i++;
            }
            //Exchange if conditions are met
            if (i<j) {
                t = arr[j];
                arr[j] = arr[i];
                arr[i] = t;
            }
 
        }
        //Finally, the datum is the digital exchange of equal position with i and j.
         arr[low] = arr[i];
         arr[i] = temp;
        //Recursive call left half array
        quickSort(arr, low, j-1);
        //Recursive call right half array
        quickSort(arr, j+1, high);
    }
 
 
    public static void main(String[] args){
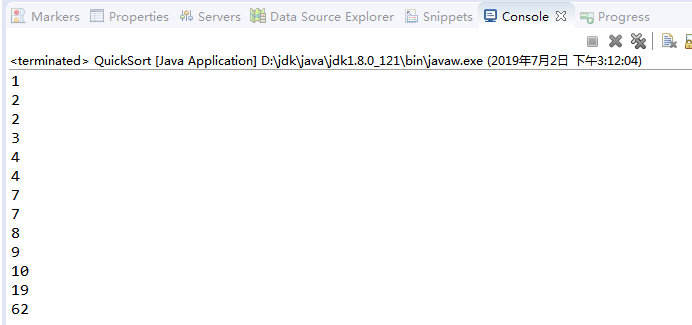
        int[] arr = {10,7,2,4,7,62,3,4,2,1,8,9,19};
        quickSort(arr, 0, arr.length-1);
        for (int i = 0; i < arr.length; i++) {
            System.out.println(arr[i]);
        }
    }
}

Result: