This chapter mainly analyzes the "insert algorithm" and "get algorithm" of red black tree, that is, the bottom implementation of put() method and get() method.
Before learning the put() method of TreeMap, we should first create a leaf node Entry class. The leaf node Entry is the internal class of TreeMap. It has several important attributes: node color, left child node pointer, right child node pointer, parent node pointer and node value.
class MyTreeMap<K, V> { // Node class class Entry<K, V> { // key K key; // value V value; // Left child Entry<K, V> left; // Right child Entry<K, V> right; // father Entry<K, V> parent; // colour boolean color = BLACK; // Construction method public Entry(K key, V value, Entry<K, V> parent) { this.key = key; this.value = value; this.parent = parent; } } }
TreeMap also contains the following important attributes:
class MyTreeMap<K, V> { // Comparator, through the comparator interface, we can precisely control the internal sorting of TreeMap private final Comparator<? super K> comparator; // Red black tree root node private Entry<K, V> root; // Container size private int size; // Node color of red black tree -- red private static final boolean RED = false; // Node color of red black tree -- black private static final boolean BLACK = true; // The Entry node class is omitted here }
Finally, we add two construction methods, one is nonparametric construction, the other is parametric construction.
class MyTreeMap<K, V> { // Omit MyTreeMap property here // Nonparametric construction method public MyTreeMap() { this.comparator = null; // Default comparison mechanism } // Parametric construction method public MyTreeMap(Comparator<? super K> comparator) { this.comparator = comparator; // Construction method of custom comparator } // The Entry node class is omitted here }
At this point, TreeMap's put() method is ready, so we will start to analyze and implement the put() method.
- **put() * * method implementation
In TreeMap's put() implementation method, there are two steps: the first step is to build a sort binary tree, and the second step is to keep the red black tree balance.
- Step 1: build a sort binary tree
For the creation of a sort binary tree, the process of adding nodes is as follows:
(1) The root node is used as the initial node for retrieval.
(2) Compared with the current node, if the value of the new node is large, the right child node of the current node is used as the new current node. Otherwise, the left child of the current node is used as the new current node.
(3) Loop recursion 2 steps until the appropriate leaf node is retrieved.
(4) Compare the new node with the node found in step 3. If the new node is large, it will be added as the right child node; otherwise, it will be added as the left child node.
Following this step, we can add a new node to the proper position in the sort binary tree. As follows:
class MyTreeMap<K, V> { // Omit MyTreeMap property and construction method here /** * Additive elements * Step 1: build a sort binary tree * Step 2: keep the balance of red and black trees */ public V put(K key, V value) { // Step 1: build a sort binary tree // 1. When the red black tree is an empty tree, set the newly created node as the following node if (null == root) { // When root is null, prove to be an empty tree // Create an Entry node and set it as the root node root = new Entry<K, V>(key, value, null); // The number of combining elements is set to 1 size = 1; return null; } // 2. If the red black number is not an empty tree, the parent node of the newly added node will be found // t represents the current node of a binary tree Entry<K, V> t = root; // Represent the parent node with parent as the parent node of the newly added node Entry<K, V> parent; // Using compare to represent the return result of key sorting int compare; // 2.1 if comparator is not null, use external comparator to create TreeMap collection if (null != comparator) { do { // parent points to t after last cycle parent = t; // Compare the size of the new node's key with the current node's key compare = comparator.compare(key, t.key); // The return value of compare is less than 0, indicating that the key of the new node is less than the key of the current node // The left child of the current node is used as the new current node if (compare < 0) { t = t.left; } // The return value of compare is greater than 0, indicating that the key of the new node is greater than the key of the current node // The right child of the current node is used as the new current node else if (compare > 0) { t = t.right; } //compare returns a value equal to 0, indicating that the two key values are equal, the new value overwrites the old value and returns the new value else { return t.value = value; } } while (null != t); // If the current node is null, the loop will jump out } // 2.2 when the comparator is null, the TreeMap set is created by natural sorting else { // Judge whether the key is empty, because the key needs to call the compareTo method if (null == key) throw new NullPointerException(); // Throw null pointer exception // The process of natural sorting is similar to that of external comparator Comparable<? super K> k = (Comparable<? super K>) key; do { parent = t; // Compare the key of the new node with the key of the current node compare = k.compareTo(t.key); if (compare < 0) { t = t.left; } else if (compare > 0) { t = t.right; } else { return t.value = value; } } while (null != t); } // 3. Insert a new node // Create a new node Entry<K, V> entry = new Entry<K, V>(key, value, parent); // If the key of the new node is less than that of the parent, it will be regarded as the left child node if (compare < 0) { parent.left = entry; } // If the key of the new node is greater than that of the parent, it will be regarded as the right child node else { parent.right = entry; } // Step 2: keep the red black tree balanced [to be implemented later in this step, omitted here] return null; } // The Entry node class is omitted here }
- Step 2: keep the balance of red and black trees
In the process of adding new nodes, the red black tree is more complex and complex. It must also be based on the five specifications mentioned above. In order to ensure that the following statements are more clear and based for reference, I will paste the five specifications of the red black tree again:
-
Each node can only be red or black.
-
The root node is black.
-
Each leaf node (NIL node, NULL null NULL node) is black.
-
The two children of each red node are black (* * * * there will be no two consecutive red nodes on the path from each leaf to the root).
-
All paths from any node to each of its leaves contain the same number of black nodes.
Since rule 1, rule 2 and rule 3 are basically satisfied, let's focus on Rule 4 and Rule 5.
Suppose we have the simplest tree here. We specify that the new node is N, its parent node is P, its sibling node is U, and its parent node is G.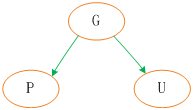
For the insertion of new nodes, there are three key points as follows:
1. Inserting a new node is always a red node.
2. If the parent of the inserted node is black, the property can be maintained.
3. If the parent of the inserted node is red, the property is broken.
Therefore, the insertion algorithm is to maintain the properties by recolor or rotation. The possible situations are as follows:
Case 1 is the follow node
If the newly inserted node N has no parent node, it can be directly inserted according to the node, and the color is set to black.
Case 2: the parent node is black
Then the inserted red node will not affect the balance of the red black tree, just insert it directly.
Case 3: both the parent node and the tertiary node are red
When the uncle node is red, there is no need to rotate. Just change the uncle and the uncle nodes to black and the grandfather nodes to red.
But after the above processing, it is possible that the parent node of the G node is also red. At this time, we need to recursively process the G node as a new node.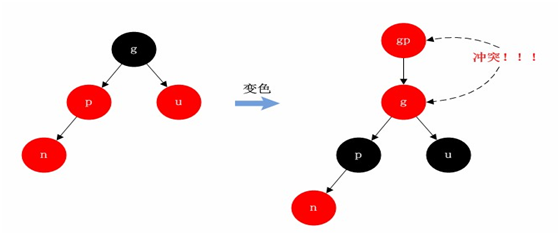
Case 4: the parent is red and tertiary black, and the new node and parent node are both left subtrees
In this case, node P is the parent node of node N and node G in the tree generated after right rotation with node P as the center.
But this tree is not standardized, so we exchange the colors of P and G nodes to make them meet the specifications.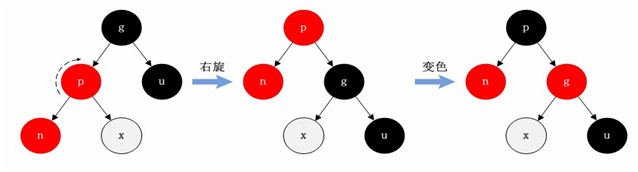
Case 5: the parent is red and tertiary black, and both the new node and the parent node are right subtrees
In this case, node P is the parent node of nodes g and N in the tree generated after the left rotation with node P as the center. But this tree is not standardized, so we exchange the colors of P and G nodes to make them meet the specifications.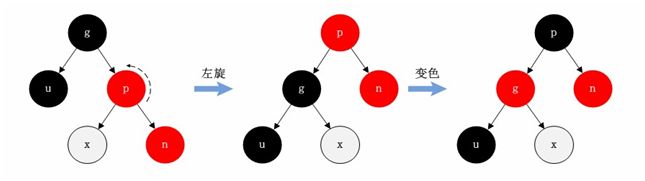
Case 6: the parent node is red and tertiary black, and the new node is the left subtree and the parent node is the right subtree
In this case, first rotate right with N node as the center. In the tree generated after rotation, node n is the parent node of nodes P and X. Then rotate left with N node as the center. In the tree generated after rotation, node n is the parent node of nodes P and G. But this tree is not standardized, so we exchange the colors of N and G nodes to make them meet the specifications.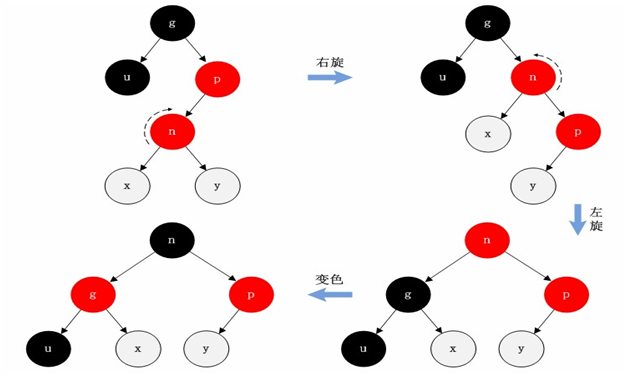
Case 7: the parent node is red and tertiary black, and the new node is the right subtree, and the parent node is the left subtree
In this case, first rotate left with N node as the center. In the tree generated after rotation, node n is the parent node of node P and Y. Then rotate right with N node as the center. In the tree generated after rotation, node n is the parent node of nodes P and G. But this tree is not standardized, so we exchange the colors of N and G nodes to make them meet the specifications.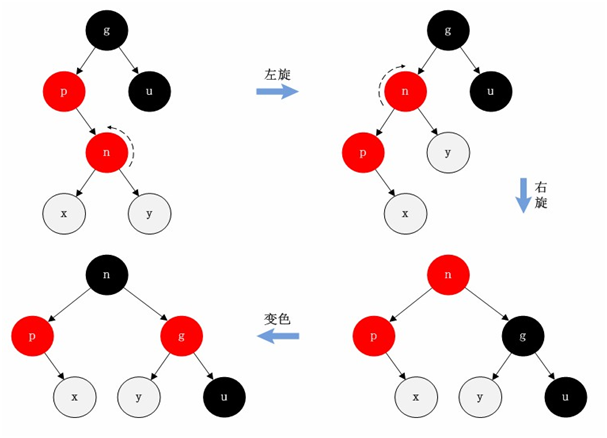
After inserting the node, the implementation of red black tree balance is maintained:
class MyTreeMap<K, V> { // Omit MyTreeMap property and construction method here /** * Additive elements * Step 1: build a sort binary tree * Step 2: keep the balance of red and black trees */ public V put(K key, V value) { // Step 1: build a sort binary tree [this step is omitted] // Step 2: keep the balance of red and black trees // Set the new node to red entry.color = RED; // Keep the balance of red and black trees fixAfterInsertion(entry); // Add element accumulation size++; return null; } /** * Keep the balance of red and black trees * When the parent node is black, the inserted red node does not affect the balance * When the parent node is red, the inserted red node will affect the balance * @param entry Indicates a new node */ private void fixAfterInsertion(Entry<K, V> entry) { // Loop until entry is not the root node, and the parent node of entry is red while (null != entry && entry != root && colorOf(entry.parent) == RED) { // When the parent node of entry belongs to the left node if (parentOf(entry) == leftOf(parentOf(parentOf(entry)))) { // Get the right uncle node of the entry Entry<K, V> uncle = rightOf(parentOf(parentOf(entry))); // When Uncle node is red (father Red & uncle red) if (colorOf(uncle) == RED) { // [situation 3] // Set parent node to black setColor(parentOf(entry), BLACK); // Set the tertiary node to black setColor(uncle, BLACK); // Set the parent of the parent to red setColor(parentOf(uncle), RED); // Update the entry and continue to traverse through the loop // Because it is possible that "parent of parent" is still red entry = parentOf(parentOf(entry)); } // When Uncle node is black (father Red & uncle black) else { // [situation iv] and [situation VII] // 1. When the new node is a right subtree (parent Red & Tertiary Black & and the new node is a right subtree & parent left subtree) if (entry == rightOf(parentOf(entry))) { // [situation 7] // Rotate the parent node of entry to the left rotateLeft(entry.parent); } // 2. When the new node is the left subtree // Parent Red & Tertiary black and new nodes and parent nodes are both left subtrees [case 4] // Set the parent node of entry to black setColor(parentOf(entry), BLACK); // Set the parent node of the entry's parent node to red setColor(parentOf(parentOf(entry)), RED); // Set the parent node of the entry parent node to right rotateRight(parentOf(parentOf(entry))); } } // When the parent node of entry belongs to the right node else { // Get the left uncle node of the entry Entry<K, V> uncle = leftOf(parentOf(parentOf(entry))); // When Uncle node is red (father Red & uncle red) if (colorOf(uncle) == RED) {// [situation 3] // Set parent node to black setColor(parentOf(entry), BLACK); // Set the tertiary node to black setColor(uncle, BLACK); // Set the parent of the parent to red setColor(parentOf(uncle), RED); // Update the entry and continue to traverse through the loop // Because it is possible that "parent of parent" is still red entry = parentOf(parentOf(entry)); } // When Uncle node is black (father Red & uncle black) else { // [situation 5] and [situation 6] // 1. When the new node is a left subtree (parent Red & Tertiary Black & and the new node is a left subtree & parent right subtree) if (entry == leftOf(parentOf(entry))) { // [situation 6] // Rotate the parent node of entry to the right rotateRight(entry.parent); } // 2. When the new node is a right subtree // Parent Red & Tertiary black and new nodes and parent nodes are both right subtrees [case 5] // Set the parent node of entry to black setColor(parentOf(entry), BLACK); // Set the parent node of the entry's parent node to red setColor(parentOf(parentOf(entry)), RED); // Set the parent node of the entry parent node to rotate left rotateLeft(parentOf(parentOf(entry))); } } } // Force the root node to black setColor(root, BLACK); } // The Entry node class is omitted here }
In order to maintain the balance of red and black trees, we need to use several important operations, such as: get parent of, get right of and left of, set color and get color of, rotate left and rotate right.
Get parent method:
/** * Get the parent node of entry */ private Entry<K, V> parentOf(Entry<K, V> entry) { return (null == entry) ? null : entry.parent; }
Get the left and right subtrees:
/** * Get the left node of the entry */ private Entry<K, V> leftOf(Entry<K, V> entry) { return (null == entry) ? null : entry.left; } /** * Get the right node of the entry */ private Entry<K, V> rightOf(Entry<K, V> entry) { return (null == entry) ? null : entry.right; }
Set and get color method:
/** * Set the color of the entry node */ private void setColor(Entry<K, V> entry, boolean color) { if (entry != null) entry.color = color; } /** * Get the color of entry node */ private boolean colorOf(Entry<K, V> entry) { // Because the default color of leaves is black return (entry == null ? BLACK : entry.color); }
Left handed method implementation: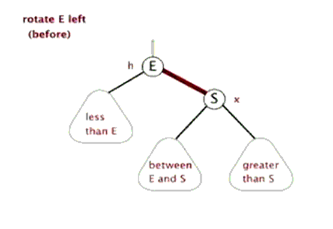
The code implementation is as follows:
/** * Left rotation */ private void rotateLeft(Entry<K, V> entry) { if (null != entry) { // 1. Get the right child node of the entry, which is equivalent to a new node Entry<K, V> right = entry.right; // 2. After left turning, set the connection between entry and right left subtree // 2.1 set the left subtree of right to the right subtree of entry // Pointing relationship: Entry -- > right.left entry.right = right.left; // 2.2 if the left subtree of right is not empty, set entry as the father of the right left subtree // Pointing relationship: right. Left -- > entry if (null != right.left) right.left.parent = entry; // // 3. After turning left, set the connection between right and entry parent nodes // 3.1 set the parent node of entry as the parent node of right // Pointing relationship: right -- > entry.parent right.parent = entry.parent; // 3.2 when entry is the root node if (null == entry.parent) { root = right; // Set right as root } // 3.3 when the entry is not the root node // Pointing relationship: entry. Parent -- > right // 3.3.1 when the entry is the left subtree of the parent node before rotation else if (entry.parent.left == entry) { entry.parent.left = right; } // 3.3.2 when the entry is the right subtree of the parent node before rotation else { entry.parent.right = right; } // 4. After turning left, set the connection between right and entry // Pointing relationship: right -- > entry right.left = entry; // Pointing relationship: Entry -- > right entry.parent = right; } }
Realization of right-handed method: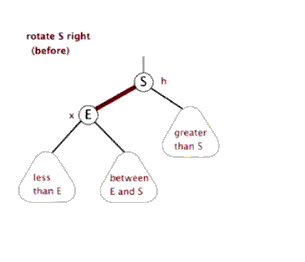
The code implementation is as follows:
/** * Right rotation */ private void rotateRight(Entry<K, V> entry) { if (null != entry) { // 1. Get the left child node of the entry, which is actually the parent node of the new node Entry<K, V> left = entry.left; // 2. After right rotation, set the connection between entry and left right subtree // Direction relationship: Entry -- > left.right; entry.left = left.right; // Pointing relationship: left. Right -- > entry if (null != left.right) { left.right.parent = entry; } // 3. After right rotation, the connection between left and its parent node // 3.1 set the connection between left and its parent node // Pointing relationship: left -- > entry.parent left.parent = entry.parent; // 3.2 when entry is a heel node // Pointing relationship: set left as root node if (null == entry.parent) { root = left; } // 3.3 when entry is not the root node // Pointing relationship: entry.parent -- > left // 3.3.1 when the entry is the left subtree else if (entry.parent.left == entry) { entry.parent.left = left; } // 3.3.2 when the entry is the right subtree else { entry.parent.right = left; } // 4. After turning right, the connection between entry and left // Pointing relationship: left -- > entry left.right = entry; // Pointing relationship: Entry -- > left entry.parent = left; } }
- **get() * * method implementation
When TreeMap fetches value according to key, the corresponding method of TreeMap is as follows:
class MyTreeMap<K, V> { // Omit MyTreeMap property and construction method here /** * Get value value according to key */ public V get(Object key) { // Get the entry object corresponding to the key Entry<K, V> p = getEntry(key); // Return the value corresponding to key return (p == null ? null : p.value); } // The Entry node class is omitted here }
From the bold code of the above program, we can see that the essence of get(Object key) method is realized by getEntry() method. The code of this getEntry() method is as follows:
/** * According to the key, get the Entry node corresponding to the key */ public Entry<K, V> getEntry(Object key) { // 1. If comparator is not null, use external comparator to create TreeMap collection if (null != comparator) { return getEntryUsingComparator(key); } // 2. Otherwise, the TreeMap set is created by natural ratio sorting // Throw NullPointerException exception when key is null if (null == key) { throw new NullPointerException(); } // Promote key up to compatible type Comparable<? super K> cmp = (Comparable<? super K>) key; // Used to save the parent node Entry<K, V> parent = root; do { // Get the return value after the compareTo method int compare = cmp.compareTo(parent.key); //When compare is less than 0, it is proved that the key is less than parent.key, then continue to search towards the left subtree of parent if (compare < 0) { // Update the value of parent parent = parent.left; } //When compare is greater than 0, it is proved that key is greater than parent.key, then continue to search for the right subtree of parent else if (compare > 0) { // Update the value of parent parent = parent.right; } // When compare is equal to 0, prove that key is equal to parent.key, then prove to find the node corresponding to key else { return parent; } } while (parent != null);//When the parent is null, the loop is ended to prove that TreeMap does not exist return null; }
The above getEntry(Object obj) method also makes full use of the characteristics of the sorted binary tree to search the target Entry. The program still starts from the root node of the binary tree. If the searched node is larger than the current node, the program searches to the "right subtree"; if the searched node is smaller than the current node, the program searches to the "left subtree"; if it is equal, the specified node is found.
When comparator! = null in TreeMap, it means that the TreeMap adopts customized sorting. In the way of customized sorting, TreeMap adopts getEntryUsingComparator(key) method to get Entry according to key.
Here is the code for this method:
public Entry<K, V> getEntryUsingComparator(Object key) { K k = (K) key; // Used to save the parent node Entry<K, V> parent = root; do { // Get the return value after compare method int compare = comparator.compare(k, parent.key); //When compare is less than 0, it is proved that the key is less than parent.key, then continue to search towards the left subtree of parent if (compare < 0) { // Update the value of parent parent = parent.left; } //When compare is greater than 0, it is proved that key is greater than parent.key, then continue to search for the right subtree of parent else if (compare > 0) { // Update the value of parent parent = parent.right; } // When compare is equal to 0, prove that key is equal to parent.key, then prove to find the node corresponding to key else { return parent; } } while (parent != null);//When the parent is null, the loop is ended to prove that TreeMap does not exist return null; }
In fact, the implementation ideas of getEntry and getEntryUsingComparator are completely similar, except that the former is effective for obtaining TreeMap of natural sorting and the latter is effective for TreeMa of customized sorting.
Through the analysis of the above source code, it is not difficult to see that the implementation of TreeMap is very simple. Or: in terms of internal structure, TreeMap is essentially a "red black tree", and each Entry of TreeMap is a node of the red black tree.
ps: Please add QQ group (627407545) to get the latest free documents and teaching videos.

