I Linked list
1. Linked list definition
A linked list is a recursive data structure. It is either empty (null) or a reference to a node that contains a generic element and a reference to another linked list.
In this definition, a node is an abstract entity that may contain any type of data type. Its applications to nodes show its usefulness in constructing linked lists.
2. Dynamic linked list
In order to represent the logical relationship between each data element ai and its direct successor element ai+1, for the data element ai, in addition to storing its own element, it also stores an information indicating its direct successor. We call the field storing data elements as data field, and the field storing direct successor positions as pointer field. The information stored in the pointer field is called a pointer or a chain. The storage image of the data element ai composed of these two parts of information is called a node; Multiple nodes are linked into a linked list, that is, the linked storage structure of linear list, as shown in the figure:
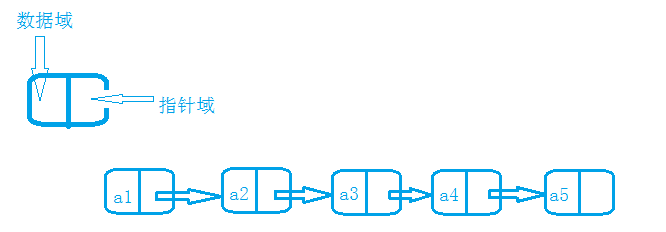
Header node and header pointer
Head node refers to the first node of the linked list, which is divided into real head node and virtual head node.
Real head node: the first node is used to store data; Virtual head node the first node does not store data.
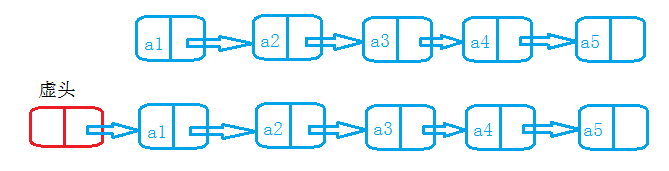
Header pointer: it is a reference variable used to store the address of the header node;
Tail pointer: also, it is the pointer of the last node in the linked list.
3. Single linked list
Single linked list is a data structure with chain access. A group of storage units with arbitrary address are used to store the data elements in the linear list. The data in the linked list is represented by nodes. The composition of each node is: element (image of data element) + pointer (indicating the storage location of subsequent elements). The element is the storage unit for storing data, and the pointer is the address data connecting each node.
3.1 code implementation
Or inherit the List interface defined by the sequence table, and then implement each function.
3.1.1 node definition
Define the Node type, adopt generic type, and define two member variables: data field and pointer field,
Then the constructors are constructed with no parameters, one parameter and two parameters.
//Define an internal class Node object
private class Node{
E data; //Data domain
Node next;//Pointer field
public Node(){
this(null,null);
}
public Node(E data){
this(data,null);
}
public Node(E data,Node next){
this.data = data;
this.next = next;
}
3.1.2 member variable definition of linked list
Define head and tail pointers, number of elements, size; The default constructor points to null at the beginning and end, and the number of elements is set to 0. Because there are no elements by default, our head and tail pointers point to null, as shown in the figure:
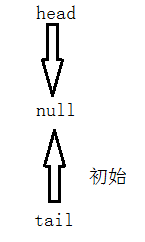
package lianbiao;
import ifce.List;
import java.util.Comparator;
import java.util.Iterator;
public class LinkedSinglyList<E> implements List<E> {
//Node inner class
@Override
public String toString() {
return data.toString();
}
}
private Node head;
private Node tail;
private int size;
public LinkedSinglyList(){
head = null;
tail = null;
size = 0;
}
3.1.3 convert an array into a linked list.
It mainly depends on the element addition method, which is to traverse the array and insert it into the linked list one by one.
public LinkedSinglyList(E[] arr){
if(arr == null || arr.length == 0){
throw new IllegalArgumentException("arr is null");
}
for(int i=0;i<arr.length;i++){
add(arr[i]);
}
}
3.1.4 adding elements
We add elements directly, and add them to the tail by default; There are also elements added according to the angle mark, so the first one can call the second one, and we implement the second one.
There are four ways to add corner markers. Of course, we first need to judge whether corner markers cross the boundary, and add them if they do not cross the boundary;
The first: add when there are no elements;
The second is added to the head;
Third, add to the tail;
The fourth is to add to the middle; Let's take a look at the following figures:


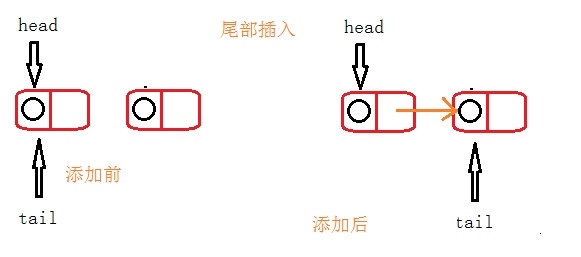
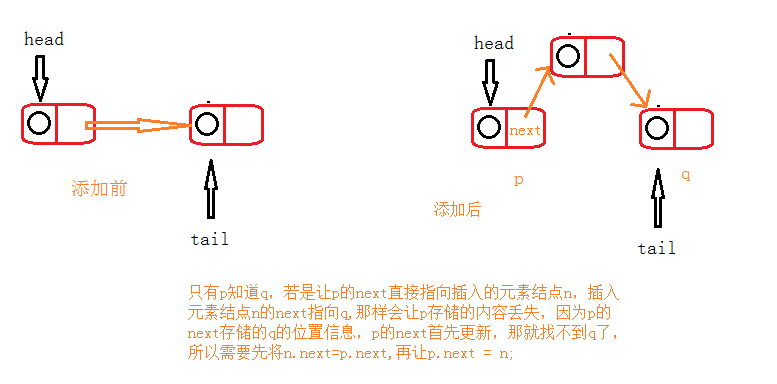
@Override
public void add(E element) {
add(size,element);
}
@Override
public void add(int index, E element) {
if(index < 0 || index > size){
throw new IllegalArgumentException("index Cross the border");
}
Node n = new Node(element);
if(size == 0){
head = n;
tail = n;
}else if(index == 0){
n.next = head;
head = n;
}else if(index == size){
tail.next = n;
tail = n;
}else{
Node p = head;
for(int i = 0;i<index-1;i++){
p = p.next;
}
n.next = p.next;
p.next = n;
}
size++;
}
3.1.5 delete element
As with adding elements, there are several cases. If the parameter is data, you can call the deletion method with the parameter as a corner mark.
First judge that the corner mark is out of range, because to return the deleted element, define a variable to save the deleted element; Then, according to the situation:
First: only one element is deleted;
The second method: delete the element from the header;
Third: delete elements from the tail;
Fourth: delete elements from the middle; Or look at the picture:
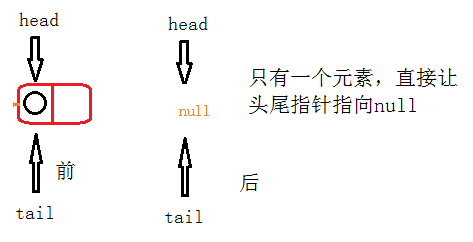

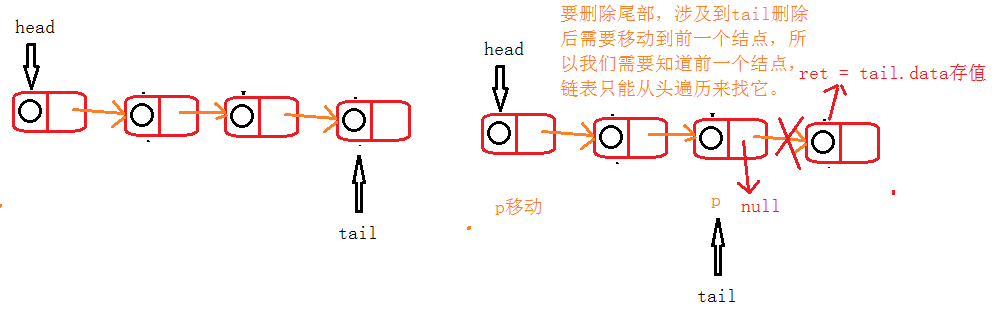
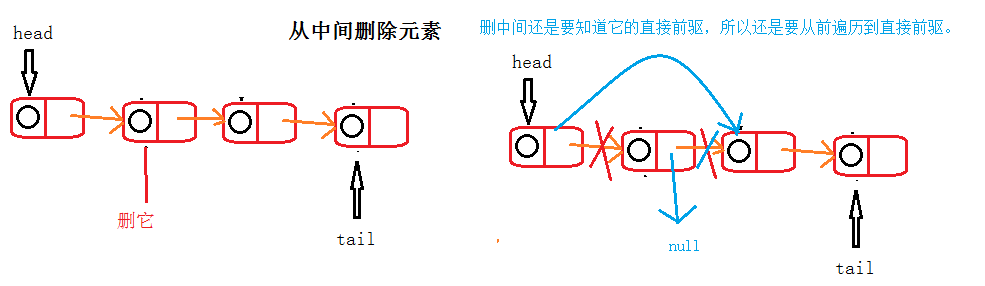
@Override
public void remove(E element) {
remove(element);
}
@Override
public E remove(int index) {
if(index < 0 || index > size){
throw new IllegalArgumentException("index Cross the border");
}
E ret = null;
if(size == 1){
ret = head.data;
head = null;
tail = null;
}else if(index == 0){
Node n = head;
ret = n.data;
head = n.next;
n.next = null;
}else if(index == size-1){
Node p = head;
while(p.next != tail){
p = p.next;
}
ret = tail.data;
p.next = null;
tail = p;
}else{
Node p = head;
for(int i = 0;i<index-1;i++){
p = p.next;
}
Node n = p.next;
p.next = n.next;
n.next = null;
}
size--;
return ret;
}
3.1.6 viewing and modifying elements through corner markers
The viewing and modifying steps are almost the same, except that viewing returns the element directly, while modifying is nothing more than defining a variable to store the value, assigning and modifying it, and then returning the saved value.
He has three situations: viewing and modifying header elements; Direct head You can get it. The tail element is through tail data. For intermediate elements, we need to traverse from 0-index, and then view or modify them.
@Override
public E get(int index) {
if(index<0|| index>=size){
throw new IllegalArgumentException("get index out of range");
}
if(index == 0){
return head.data;
}else if(index == size - 1){
return tail.data;
}else{
Node p = head;
for(int i = 0;i<index;i++){
p=p.next;
}
return p.data;
}
}
@Override
public E set(int index, E element) {
if(index<0|| index>=size){
throw new IllegalArgumentException("get index out of range");
}
E ret = null;
if(index == 0){
ret = head.data;
head.data = element;
}else if(index == size - 1){
ret = tail.data;
tail.data = element;
}else{
Node p = head;
for(int i = 0;i<index;i++){
p=p.next;
}
ret = p.data;
}
return ret;
}
3.1.7 angle finding through elements
Define a subscript, traverse from the head node, traverse backward as long as the elements are unequal, and then add 1 to the subscript. If it is not found after traversal, return - 1; If found, return the corresponding subscript.
@Override
public int indexOf(E element) {
Node p = head;
int index = 0;
while (!p.data.equals(element)){
p = p.next;
index++;
if(p == null){
return -1;
}
}
return index;
}
3.1.8 sorting
Selective sorting is used; Define two pointer nodes. The outer loop starts from the head and ends at the penultimate element. The inner loop starts at the next node of the head and ends at the last node.
@Override
public void sort(Comparator<E> c) {
if(c == null){
throw new IllegalArgumentException("comparator is null");
}
if(size == 0 || size == 1){
return;
}
Node nodeA = head;
Node nodeB = nodeA.next;
while (true){
while (true){
if(c.compare(nodeA.data,nodeB.data)>0){
swap(nodeA,nodeB);
}
if(nodeB == tail){
break;
}
nodeB = nodeB.next;
}
if(nodeA.next == tail){
break;
}
nodeA = nodeA.next;
nodeB = nodeA.next;
}
}
private void swap(Node nodeA, Node nodeB) {
E temp = nodeA.data;
nodeA.data = nodeB.data;
nodeB.data = temp;
}
3.1.9 cutting substring
Because we implement a one-way linked list, we can't traverse forward, so we need to traverse from front to back to find an element; Find the fromIndex and toIndex corresponding positions in the linked list. Then add them to the linked list one by one.
@Override
public List<E> subList(int fromIndex, int toIndex) {
if(fromIndex<0 || toIndex>=size|| fromIndex > toIndex){
throw new IllegalArgumentException("must 0 <= fromIndex <= toIndex <= size - 1");
}
LinkedSinglyList<E> list = new LinkedSinglyList<>();
Node nodeA = head;
for(int i = 0;i<fromIndex;i++){
nodeA = nodeA.next;
}
Node nodeB = head;
for(int i = 0;i<toIndex;i++){
nodeB = nodeB.next;
}
Node p = nodeA;
while(true){
list.add(p.data);
if(p == nodeB){
break;
}
p = p.next;
}
return list;
}
3.1.10 toString method, and the implementation of iterator.
tostring is similar to a sequence table. The iterator defines that the face change points to the head node. As long as the variable does not point to null, it indicates that there is an element. Then, let the corner mark move once and return the corresponding value.
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("[");
if (isEmpty()) {
sb.append("]");
} else {
Node p = head;
while (true) {
sb.append(p.data);
if (p == tail) {
sb.append("]");
break;
}
sb.append(",");
sb.append(" ");
p = p.next;
}
}
return sb.toString();
}
@Override
public Iterator<E> iterator() {
return new LinkedSinglyListIterator();
}
class LinkedSinglyListIterator implements Iterator<E>{
private Node cur = head;
@Override
public boolean hasNext() {
return cur != null;
}
@Override
public E next() {
E ret = cur.data;
cur = cur.next;
return ret;
}
}
3.1.11 other methods
@Override
public int size() {
return size;
}
@Override
public boolean contains(E element) {
return indexOf(element) != -1;
}
@Override
public boolean isEmpty() {
return size == 0 && head == null && tail == null;
}
@Override
public void clear() {
head = null;
tail = null;
size = 0;
}
3. One way circulation linked list
He added a little improvement on the basis of the one-way linked list, mainly to make our linked list traverse the tail and return to the head to form a ring. Some methods are improved on the basis of single linked list, so we change the code;
The method to modify the code is as follows:
@Override
public void add(int index, E element) {
if(index < 0 || index > size){
throw new IllegalArgumentException("index Cross the border");
}
Node n = new Node(element);
if(size == 0){
head = n;
tail = n;
tail.next = head;//new code links the end of the list to the head.
}else if(index == 0){
n.next = head;
head = n;
tail.next = head;//new code
}else if(index == size){
n.next = tail.next; //new code
tail.next = n;
tail = n;
}else{
Node p = head;
for(int i = 0;i<index-1;i++){
p = p.next;
}
n.next = p.next;
p.next = n;
}
size++;
}
@Override
public E remove(int index) {
if(index < 0 || index > size){
throw new IllegalArgumentException("index Cross the border");
}
E ret = null;
if(size == 1){
ret = head.data;
head = null;
tail = null;
}else if(index == 0){
Node n = head;
ret = n.data;
head = n.next;
n.next = null;
tail.next = head;//new code
}else if(index == size-1){
Node p = head;
while(p.next != tail){
p = p.next;
}
ret = tail.data;
p.next = tail.next;//change code originally pointed to null, because the next element at the end of the one-way linked list is null. For our one-way circular linked list, the next element of the last element is head;
tail = p;
}else{
Node p = head;
for(int i = 0;i<index-1;i++){
p = p.next;
}
Node n = p.next;
p.next = n.next;
n.next = null;
}
size--;
return ret;
}
@Override
public int indexOf(E element) {
Node p = head;
int index = 0;
while (!p.data.equals(element)){
p = p.next;
index++;
if(p == head){ //change code is the same. The last element of the single linked list points to null, while the one-way circular linked list points to head.
return -1;
}
}
return index;
}
@Override
public Iterator<E> iterator() {
return new LinkedSinglyCircularListIterator();
}
class LinkedSinglyCircularListIterator implements Iterator<E>{
private Node cur = head;//Determine whether there are elements according to the number of turns
private boolean flag = true;
@Override
public boolean hasNext() {
if(isEmpty()){
return false;
}//It is established when the linked list is not empty
return flag;
}
@Override
public E next() {
E ret = cur.data;
cur = cur.next;
if(cur == head){
flag = false;
}
return ret;
}
}
}
test
Traverse the directory structure and print the directory name and the directory or file name under the directory.
public class TestLinkedSinglyList {
public static void main(String[] args) {
LinkedSinglyCircularList<Integer> list = new LinkedSinglyCircularList();
list.add(1);
list.add(5);
list.add(3);
list.add(9);
list.add(4);
list.add(8);
System.out.println(list.toString());
list.sort(new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o1 - o2;
}
});
System.out.println(list);
}
}
4. Two way circular linked list LinkedList
Bidirectional circular linked list is a kind of linked list. Each data node of it has two pointers, pointing to the direct successor and direct precursor respectively. So we can traverse our linked list from front to back. As shown in the figure:

4.1 node type definition
Or define an internal class of Node type, define the precursor pointer pre, the successor pointer next, the data field data, our construction method, and the toString method to return data.
class Node{
E data;
private Node pre;
private Node next;
public Node(){
this(null,null,null);
}
public Node(E data){
this(data,null,null);
}
public Node(E data,Node pre,Node next){
this.data = data;
this.pre = pre;
this.next = next;
}
@Override
public String toString() {
return data.toString();
}
}
4.2 definition and construction method of LinkedList member variable
Define the head and tail nodes, as well as the number of elements and size attribute; Parameterless construction is to create a default linked list, which is empty by default, so head and tail point to null and size is 0; Another construction method with parameters passes in an array and converts it into a linked list. We directly take out each element in the array and add it to the linked list one by one.
public class LinkedList<E> implements List<E>, Deque<E>, Stack<E> {
private Node head;
private Node tail;
private int size;
public LinkedList(){
head = null;
tail = null;
size = 0;
}
public LinkedList(E[] arr){
if(arr == null){
throw new IllegalArgumentException("arr is null");
}
for(int i = 0;i<arr.length;i++){
add(arr[i]);
}
}
4.3 adding elements
First judge that the angle marker is out of range, and then discuss it according to the situation:
The first: add when there are no elements;
Second: add from the head;
Third: add from the tail;
Fourth: add from the middle;
The first is relatively simple: since the default head and tail point to null, it is good to directly point them to new elements, and then establish a loop to point the precursor of head to tail and the direct successor of tail to head;
Second:
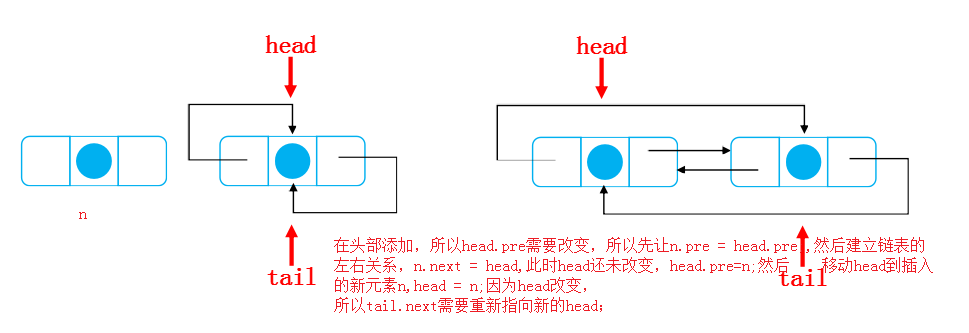
The third is similar to the second. It's upside down.
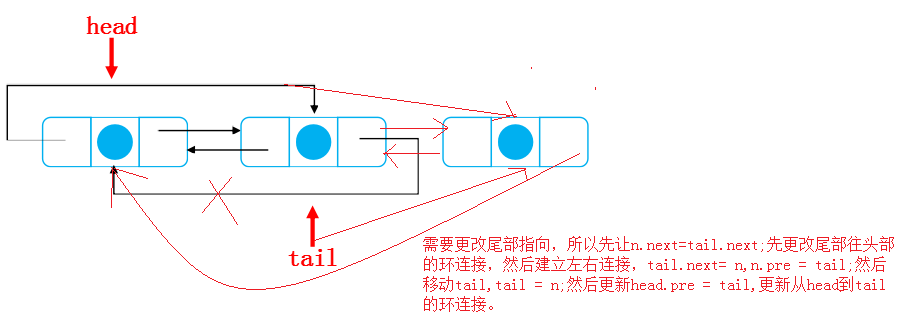
Fourth:

@Override
public void add(E element) {
add(size,element);
}
@Override
public void add(int index, E element) {
if(index < 0 || index > size){
throw new IllegalArgumentException("index out of range");
}
Node n = new Node(element);
if(size == 0){
head = n;
tail = n;
tail.next = head;
head.pre = tail;
}else if(index == 0){
n.pre = head.pre;
n.next = head;
head.pre = n;
head = n;
tail.next = head;
}else if(index == size){
tail.next = n.next;
tail.next = n;
n.pre = tail;
tail = n;
head.pre = tail;
}else{
Node p,q;
if(index <= size / 2){
p = head;
for(int i = 0;i<index-1;i++){
p = p.next;
}
q = p.next;
p.next = n;
n.pre = p;
q.pre = n;
n.next = q;
}else {
p = tail;
for(int i = size -1;i> index;i--){
p = p.pre;
}
q = p.pre;
q.next = n;
n.pre =q;
n.next = p;
p.pre = n;
}
}
size++;
}
4.4 deleting elements
Deleting elements is similar to adding elements, but some are different.
The first: if there is only one element, the deletion becomes an empty linked list, so directly let the head and tail nodes point to null;
Second: delete from header:
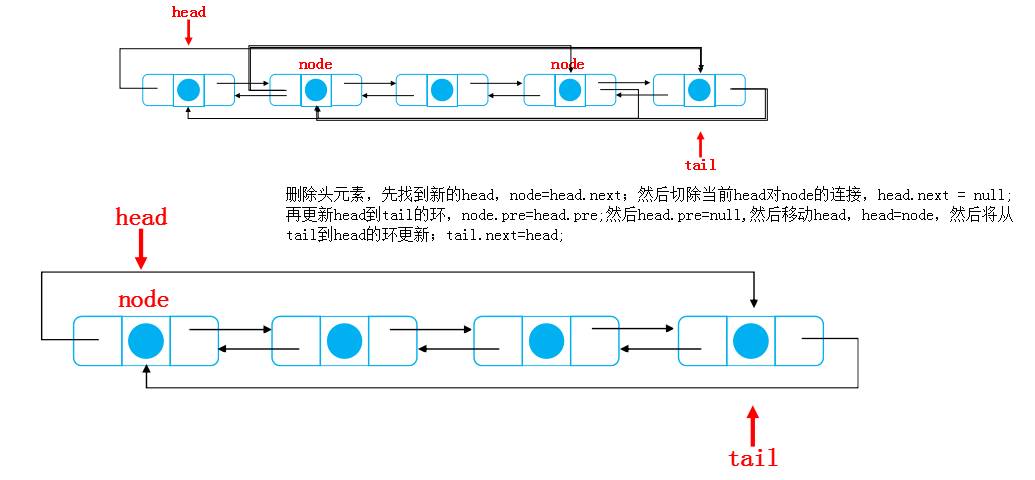
The third is the reverse of the second;
Find a new tail first, node = tail pre; Then disconnect the tail from the node; tail.pre = null; Then update the link from tail to head, node next = tail. Next, disconnect the tail from the head, tail next =null; Update the tail again; tail=node; Then update the link from head to tail; head.pre = tail.
@Override
public void remove(E element) {
int index = indexOf(element);
if(index != -1){
remove(index);
}
}
@Override
public E remove(int index) {
if(index < 0 || index >= size){
throw new IllegalArgumentException("index out of range");
}
E ret = null;
Node node;
if(size == 1){
ret = head.data;
head = null;
tail = null;
}else if(index == 0){
ret = head.data;
node = head.next;
head.next = null;
node.pre = head.pre;
head.pre = null;
head = node;
tail.next = head;
}else if(index == size-1){
ret = tail.data;
node = tail.pre;
tail.pre = null;
tail.next = node.next;
tail.next = null;
tail = node;
head.pre = tail;
}else {
Node p,q,r;
if(index <= size/2){
p = head;
for(int i=0;i< index -1;i++){
p = p.next;
}
q = p.next;
r = q.next;
ret = q.data;
p.next = r;
r.pre =p;
q.next = null;
q.pre = null;
}else {
p = tail;
for(int i=size-1;i< index +1;i--){
p = p.pre;
}
q = p.pre;
r = q.pre;
ret = q.data;
r.next = p;
p.pre = r;
q.pre = null;
q.next = null;
}
}
size--;
return ret;
}
4.5 viewing and modifying elements through corner markers
First judge whether the corner marker is out of bounds, then check the head, and return to head Data, view the tail, and return to tail Data, check the intermediate elements, traverse from 0 to the corner index, find the corresponding node, and then return its elements;
Modification is nothing more than saving the corresponding data, then modifying the value of the element, and finally returning the value.
@Override
public E get(int index) {
if(index < 0 || index >= size){
throw new IllegalArgumentException("index out of rang");
}
if(index == 0){
return head.data;
}else if(index == size-1){
return tail.data;
}else{
Node p = head;
for(int i = 0;i<index;i++){
p = p.next;
}
return p.data;
}
}
@Override
public E set(int index, E element) {
if(index < 0 || index >= size){
throw new IllegalArgumentException("index out of rang");
}
E ret = null;
if(index == 0){
ret = head.data;
head.data = element;
}else if(index == size-1){
ret = tail.data;
tail.data = element;
}else{
Node p = head;
for(int i = 0;i<index;i++){
p = p.next;
}
ret = p.data;
}
return ret;
}
4.6 sorting method
First judge whether the constructor is null, and then the linked list has only one element or no element, so there is no need to sort. We use insert sort;
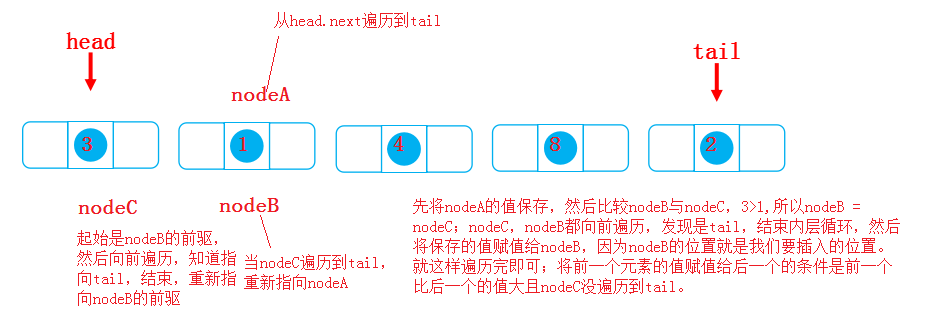
@Override
public void sort(Comparator<E> c) {
if(c == null){
throw new IllegalArgumentException("comparator is null");
}
if(size == 0 || size == 1){
return;
}
for (Node nodeA = head.next;nodeA != head;nodeA = nodeA.next){
E e = nodeA.data;
Node nodeB,nodeC;
for(nodeB = nodeA,nodeC=nodeB.pre; nodeC != tail && c.compare(nodeC.data,e)>0;nodeB=nodeB.pre,nodeC=nodeC.pre){
nodeB.data = nodeC.data;
}
nodeB.data = e;
}
}
4.7 stack method
The stack calls the method of queue to realize its own operation.
@Override
public void push(E element) {
addLast(element);
}
@Override
public E pop() {
return removeLast();
}
@Override
public E peek() {
return getLast();
}
4.8 methods for queues
The Queue method is mainly implemented through Deque, which calls the addition, deletion and query method of our LinkedList
@Override
public void offer(E element) {
addLast(element);
}
@Override
public E poll() {
return removeFirst();
}
@Override
public E element() {
return getFirst();
}
//Deque
@Override
public void addFirst(E element) {
add(0,element);
}
@Override
public void addLast(E element) {
add(size,element);
}
@Override
public E removeFirst() {
return remove(0);
}
@Override
public E removeLast() {
return remove(size-1);
}
@Override
public E getFirst() {
return get(0);
}
@Override
public E getLast() {
return get(size-1);
}
4.9 other methods
The method here is as like as two peas in our one-way loop list.
@Override
public int size() {
return size;
}
@Override
public int indexOf(E element) {
Node p = head;
int index = 0;
while (!p.data.equals(element)){
p=p.next;
index++;
if(p == head){
return -1;
}
}
return index;
}
@Override
public boolean contains(E element) {
return indexOf(element) != -1;
}
@Override
public boolean isEmpty() {
return size == 0 && head==null && tail == null;
}
@Override
public void clear() {
head = null;
tail = null;
size = 0;
}
@Override
public List<E> subList(int fromIndex, int toIndex) {
if(fromIndex<0 || toIndex >= size || fromIndex < toIndex){
throw new IllegalArgumentException("0<=fromIndex<=toIndex<=size-1");
}
Node nodeA = head;
for(int i = 0;i<fromIndex;i++){
nodeA = nodeA.next;
}
Node nodeB = head;
for(int i = 0;i<toIndex;i++){
nodeB = nodeB.next;
}
Node p = nodeA;
LinkedList<E> list = new LinkedList<>();
while(true){
list.add(p.data);
if(p == nodeB){
break;
}
p = p.next;
}
return list;
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("[");
if (isEmpty()) {
sb.append("]");
} else {
Node p = head;
while (true) {
sb.append(p.data);
if (p == tail) {
sb.append("]");
break;
}
sb.append(",");
sb.append(" ");
p = p.next;
}
}
return sb.toString();
}
@Override
public Iterator<E> iterator() {
return new LinkedListIterator();
}
class LinkedListIterator implements Iterator<E>{
private Node cur = head;
private boolean flag = true;
@Override
public boolean hasNext() {
if(isEmpty()){
return false;
}//It is established when the linked list is not empty
return flag;
}
@Override
public E next() {
E ret = cur.data;
cur = cur.next;
if(cur == head){
flag = false;
}
return ret;
}
}