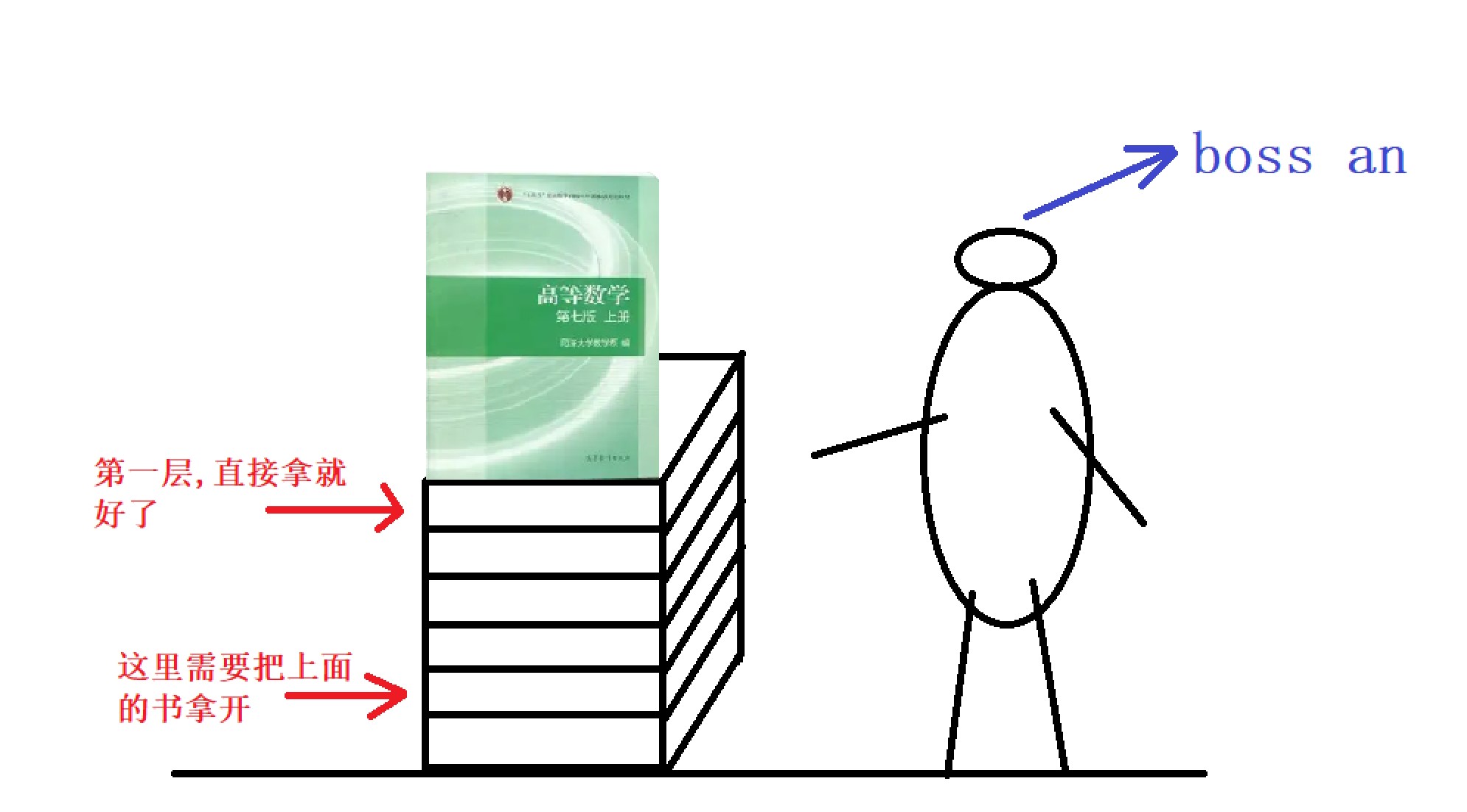
In life, we often encounter such situations: 1. When someone sends a book at school, if he wants to take out the top book, he can take it out directly. However, if he wants to take out the book in the middle, he must remove the book pressed on it to see the book. At this time, only the top can be taken out first, and the bottom can be taken out later.
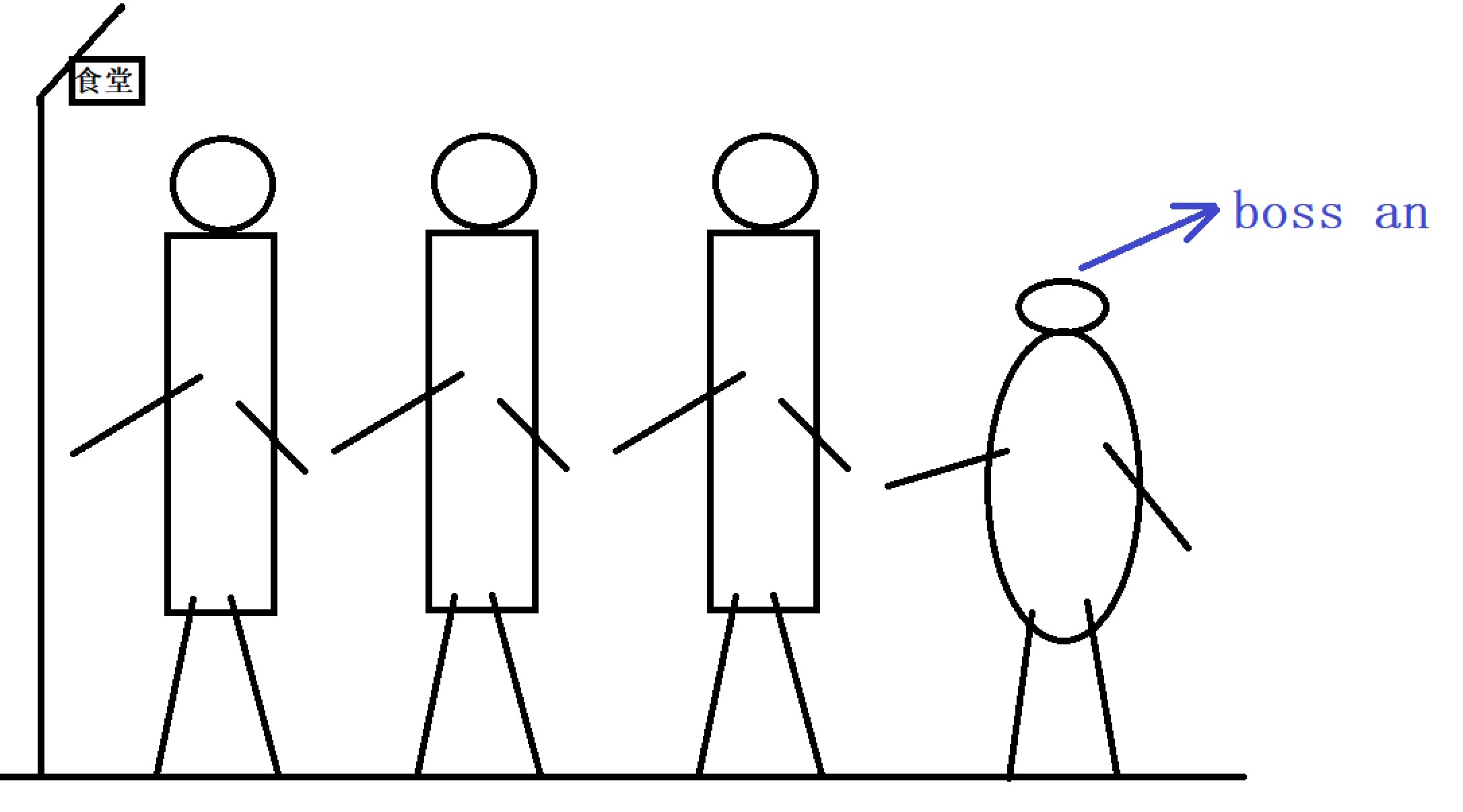
2. After class, someone goes to the school canteen for dinner. When there are many people, he needs to queue up. Suppose there is no queue jumping. Then if he wants to eat, he must wait for the people in front of him to finish, and he can't eat until his time. At this time, those who line up first go first, and those who line up later go later.
The above two cases correspond to two data structures in the data structure: stack and queue. The most important feature of the former is the first in and last out, while the most important situation of the latter is the first in and first out. Here are the characteristics and differences between the two.
1, stack
1. Concept
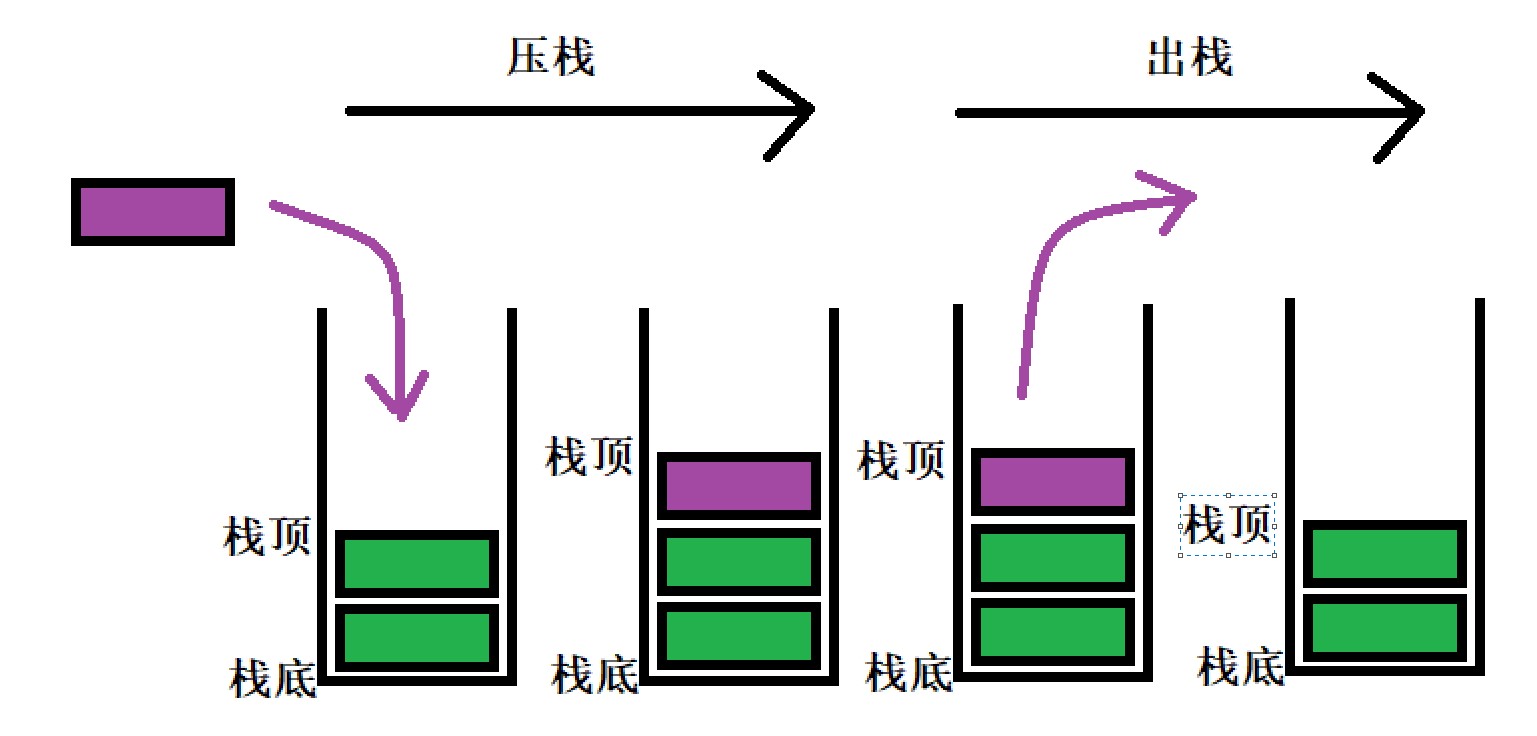
Stack is a special linear table, which only allows the insertion and deletion of elements at the fixed end. One end for data insertion and deletion is called the top of the stack, and the other end is called the bottom of the stack. The data elements in the stack follow the principle of Last In First Out LIFO (Last In First Out).
Stack pressing: the stack insertion operation is called stack entering / stack pressing / stack entering, and the input data is at the top of the stack.
Stack out: stack deletion is called stack out. The output data is at the top of the stack.
The underlying principle of stack implementation is sequence list or linked list. Here, we use sequence list to realize some operations of stack, such as pressing stack, getting out of stack, checking the elements at the top of stack and judging whether the stack is empty. If you use the sequence table, you only need to insert and delete the tail. Head plug deletion is also OK, but in this case, the time complexity is high, while tail insertion and tail deletion only requires the time complexity of o (1).
2. Realize some operations of the stack by yourself
1) Basic properties
Assuming that it stores integer elements, first define an array array of int type. At the same time, it can be seen from the above figure that there is a stack top, which is simply the effective size of an array. Then we are defining an int variable top to store the effective size of the array. Here, we assume that the size of the array is 10.
class stack {
private int[] array;
private int top;
//The appropriate construction method is to initialize the array. At the beginning, the top has no elements and is 0;
public stack() {
this.array = new int[10];
}
}2) push
When we pass in a value val, we must first judge whether the table is full. If so, we must expand the capacity. If not, after putting in the element, let top add it once.
//Stack pressing operation
public void push(int val) {
if(this.array.length == this.top) {
this.array = Arrays.copyOf(this.array, 2 * this.array.length);
}
this.array[top] = val;
top++;
}3) empty
Judge whether top is 0 or not.
//Is it empty
public boolean empty() {
return this.top == 0;
}4) Out of stack (pop)
Out of the stack, pop up the element at the top of the stack, and accept it with a variable. First judge whether it is empty. If it is empty, throw an exception. If not, return the element at the top of the stack and directly reduce the top by one.
//Stack out operation
public int pop() {
if(empty()) {
throw new UnsupportedOperationException("Stack is empty!");
}
int ret = this.array[this.top - 1];//subscript
this.top--;//top minus one
return ret;
}5) View stack top element (peek)
Similar to 4), you just need to view it, but you don't need to reduce the top by one.
//View the top element of the stack without pop-up
public int peek() {
if(empty()) {
throw new UnsupportedOperationException("Stack is empty!");
}
int ret = this.array[this.top - 1];
return ret;
}The results are as follows:
import java.util.Arrays;
class stack {
//encapsulation
private int[] array;
private int top;
//The appropriate construction method is to initialize the array. The default value of top is 0;
public stack() {
this.array = new int[10];
}
//Stack pressing operation
public void push(int val) {
if(this.array.length == this.top) {
this.array = Arrays.copyOf(this.array, 2 * this.array.length);
}
this.array[top] = val;
top++;
}
//Stack out operation
public int pop() {
if(empty()) {
throw new UnsupportedOperationException("Stack is empty!");
}
int ret = this.array[this.top - 1];
this.top--;
return ret;
}
//Is it empty
public boolean empty() {
return this.top == 0;
}
//View the top element of the stack without pop-up
public int peek() {
if(empty()) {
throw new UnsupportedOperationException("Stack is empty!");
}
int ret = this.array[this.top - 1];
return ret;
}
}
public class Main {
public static void main(String[] args) {
stack stack = new stack();
stack.push(1);
stack.push(2);
stack.push(3);
System.out.println(stack.peek());//3
stack.pop();
System.out.println(stack.peek());//2
System.out.println(stack.empty());//false
}
}3. Some operations of officially encapsulated stack
Java has encapsulated these data structures. You can directly import the appropriate package to call. If you are interested, you can check the help manual of Java or the source code of these methods. Stack (Java Platform SE 8 ) (oracle.com)
https://docs.oracle.com/javase/8/docs/api/java/util/Stack.html#push-E-
import java.util.Arrays;
import java.util.Stack;
public class Main {
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();//Package to import
stack.push(1);
stack.push(2);
stack.push(3);
System.out.println(stack.peek());//3
stack.pop();
System.out.println(stack.peek());//2
System.out.println(stack.empty());//false
}
}2, Queue
(1) , queue
1. Concept
Queue: a special linear table that only allows inserting data at one end and deleting data at the other end. The queue has first in first out FIFO(First In First Out). Queue entry: the end of the insertion operation is called tail / rear. Out of queue: the end of the deletion operation is called the queue head. (Head/Front)
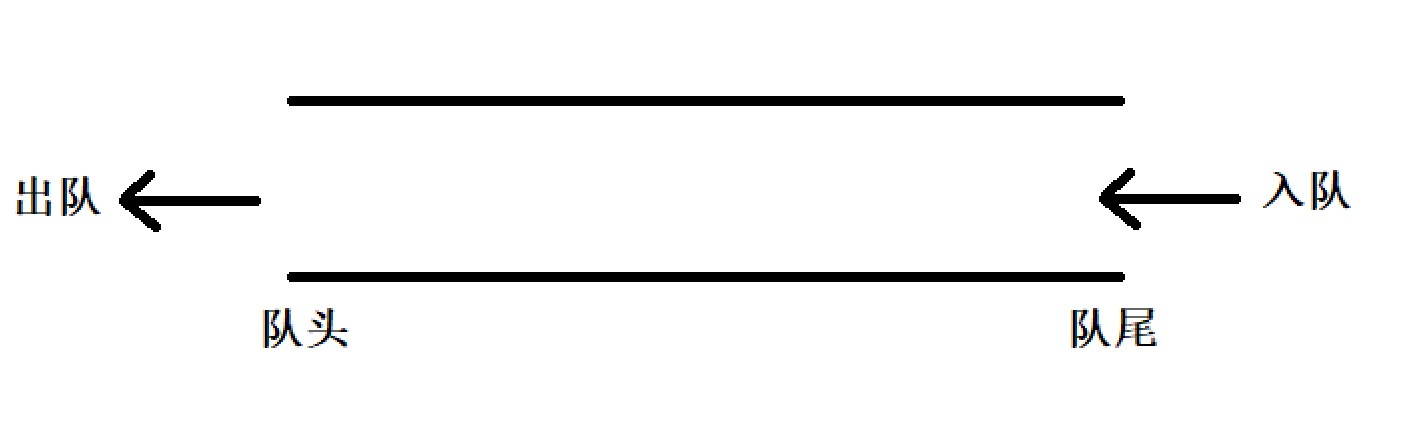
2. Implement some operations of the queue by yourself
Queues can also be implemented in the structure of arrays and linked lists. It is better to use the structure of linked list, because if the structure of array is used, the data will be sent out from the queue on the head of the array, and the efficiency will be relatively low. And stack have similar operations. We use single linked list.
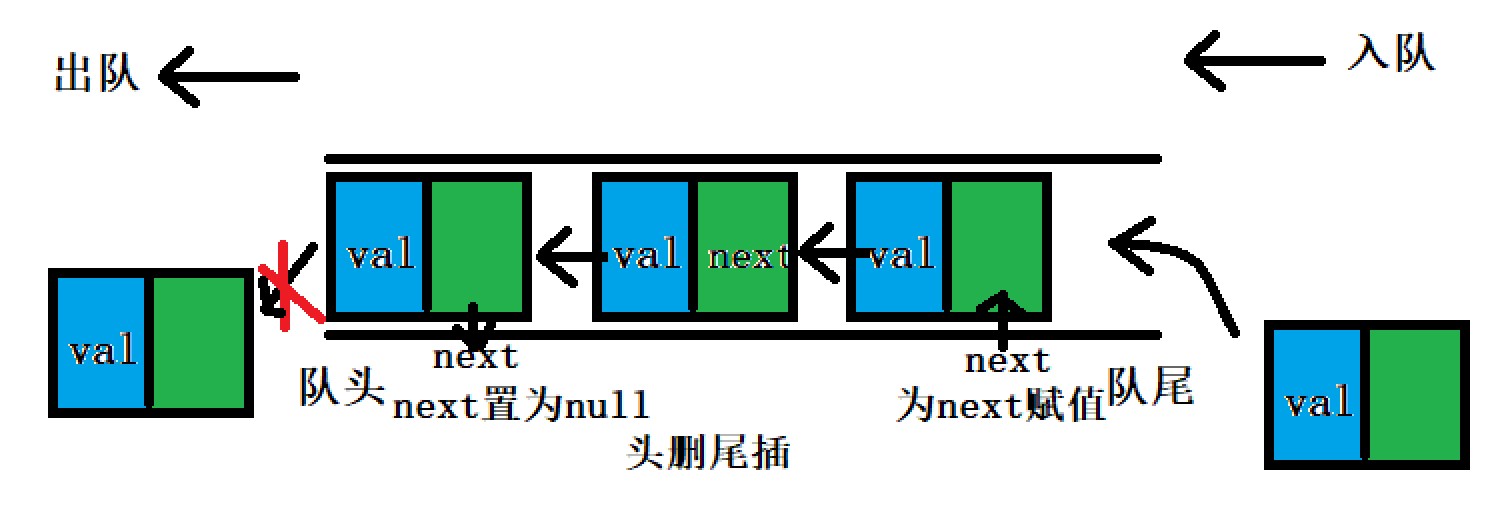
1) Basic attributes
Here, it is assumed to store the element of integer type, set the class name as Node, define an element val of int type, and define a reference type Node type element next. Which stores the address of the next element.
class Node {
//Private permissions can also be set to public, which is more direct
private int val;
private Node next;
public Node(int val) {
this.val = val;
}
public int getVal() {
return val;
}
public void setVal(int val) {
this.val = val;
}
public Node getNext() {
return next;
}
public void setNext(Node next) {
this.next = next;
}
}2) offer
We pass in a value val and set two pointers first and last to store the addresses of the head and tail respectively. First, we should judge whether this node is inserted for the first time. If so, let first and last point to this node at the same time. If not, after putting in the element, let the last point to the address of the inserted element.
class queue {
private Node first;
private Node last;
//Join the team
public void offer(int val) {
Node node = new Node(val);
if(this.first == null) {
this.first = node;
this.last = node;
} else {
this.last.setNext(node);
this.last = node;
}
}
}3) Is it empty (isEmpty)
Judge whether the first point is empty.
//Is it empty
public boolean isEmpty() {
return this.first == null;
}4) poll
First judge whether it is empty. If yes, throw an exception. If not, after obtaining the element, let first directly point to the next element.
//Out of the team
public int poll() {
if(isEmpty()) {
throw new UnsupportedOperationException("The queue is empty!");
}
int ret = this.first.getVal();
this.first = this.first.getNext();
return ret;
}5) Get the team head element but don't delete it
Similar to 4), but do not need to move first.
//Get the team head element but don't delete it
public int peek() {
if(isEmpty()) {
throw new UnsupportedOperationException("The queue is empty!");
}
int ret = this.first.getVal();
return ret;
}The results are as follows:
class Node {
//Private rights
private int val;
private Node next;
public Node(int val) {
this.val = val;
}
public int getVal() {
return val;
}
public void setVal(int val) {
this.val = val;
}
public Node getNext() {
return next;
}
public void setNext(Node next) {
this.next = next;
}
}
class queue {
private Node first;
private Node last;
//Join the team
public void offer(int val) {
Node node = new Node(val);
if(this.first == null) {
this.first = node;
this.last = node;
} else {
this.last.setNext(node);
this.last = node;
}
}
//Out of the team
public int poll() {
if(isEmpty()) {
throw new UnsupportedOperationException("The queue is empty!");
}
int ret = this.first.getVal();
this.first = this.first.getNext();
return ret;
}
//Get the header element but not delete it
public int peek() {
if(isEmpty()) {
throw new UnsupportedOperationException("The queue is empty!");
}
int ret = this.first.getVal();
return ret;
}
//Is it empty
public boolean isEmpty() {
return this.first == null;
}
}
public class Main {
public static void main(String[] args) {
queue queue = new queue();
queue.offer(1);
queue.offer(2);
queue.offer(3);
System.out.println(queue.peek());//1
queue.poll();
System.out.println(queue.peek());//2
System.out.println(queue.isEmpty());//false
}
}3. Some operations of the officially encapsulated queue
https://docs.oracle.com/javase/8/docs/api/java/util/Queue.htmlpublic class Main {
public static void main(String[] args) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(1);
queue.offer(2);
queue.offer(3);
System.out.println(queue.peek());//1
queue.poll();
System.out.println(queue.peek());//2
System.out.println(queue.isEmpty());//false
}
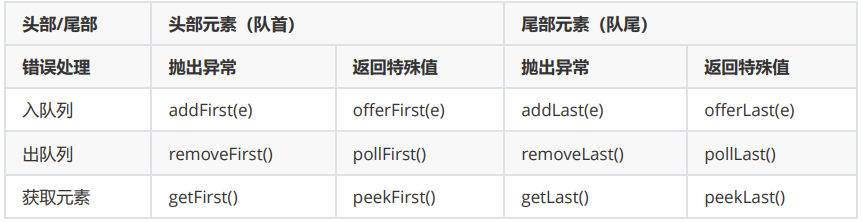
}(2) , dual ended queue (Deque)
Double ended queue is a queue that allows both ends to enter and leave the queue. Elements can be out of the team and in the team from the head of the team, or out of the team and in the team from the end of the team. Let's look directly at Java's encapsulation of these operations. If you are interested, you can read its source code.
(3) Circular queue
In practice, we will encounter a kind of queue called circular queue. We illustrate this with static queues.
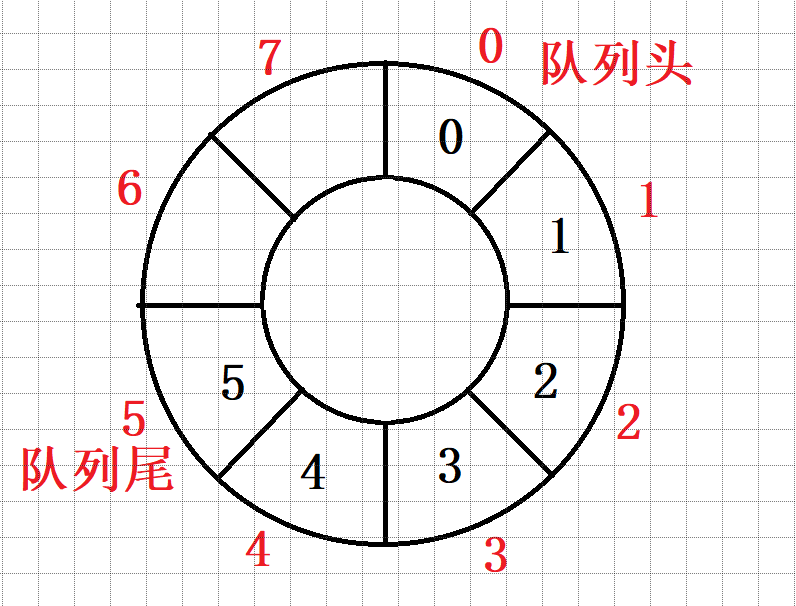
Sometimes, we pop up the elements at the head of the team, and then add new elements. Just add them directly at the end of the team. If an array is full, the first thing to think of is capacity expansion. But when we look again, we find that the pop-up position in front is empty.
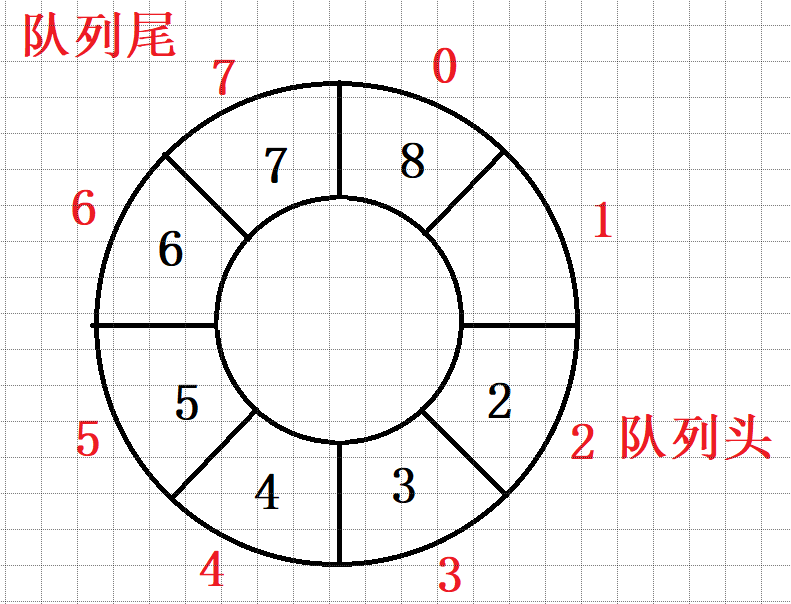
This will greatly save space. Next, we use arrays to implement a circular queue ourselves.
1) Basic properties
As can be seen from the above figure, a circular queue should at least contain an array (elem), a front and a rear. We encapsulate it in the MyCircularQueue class. Provide an appropriate construction method (MyCircularQueue). In this construction method, define the size of the array, the subscript of the team head and the subscript of the team tail.
class MyCircularQueue {
private int[] elem;//array
private int front;//Header subscript
private int rear;//Tail subscript
public MyCircularQueue(int k) {
this.elem = new int[k];
this.rear = 0;
this.front = 0;
}
}2) Enter queue
In each step of the queue entry operation, it is necessary to judge whether the queue is full. If it is full, an error will be reported. If not, put the element into the space of the tail subscript, and add 1 to the tail subscript. But we can't add it directly here. From the above situation, we can know that putting 8 in the subscript 0, where the real is originally the subscript 7, and it is obviously out of bounds at + 1. Minor changes are required. Change to:
this.rear = (this.rear + 1) % this.elem.length; (length of array)
public boolean enterQueue(int val) {
if(isFull()) {
return false;
}
this.elem[this.rear] = val;
this.rear = (this.rear + 1) % this.elem.length;
return true;
} public boolean isFull() {
return (this.rear + 1) % this.elem.length == this.front;
}3) Out of queue (deleteQueue)
Judge whether it is empty. If not, let the head subscript + 1.
public boolean deleteQueue() {
if(isEmpty()) {
return false;
}
this.front = (this.front + 1) % this.elem.length;
return true;
} public boolean isEmpty() {
//When you meet, you are an empty queue. If you don't understand, you can draw a picture
return this.front == this.rear;
}4) Get the team head element (Front)
public int Front() {
if(isEmpty()) {
return -1;
}
return this.elem[this.front];
}5) Get the tail element (Rear)
It should be noted that if the rear reaches the maximum capacity, at + 1, it reaches the subscript 0, which needs to be considered.
public int Rear() {
if(isEmpty()) {
return -1;
}
//When rear reaches 0 subscript
int index = (this.rear == 0) ? this.elem.length - 1 : this.rear - 1;
return this.elem[index];
}All codes are as follows:
class MyCircularQueue {
private int[] elem;//array
private int front;//Header subscript
private int rear;//Tail subscript
public MyCircularQueue(int k) {
this.elem = new int[k];
this.rear = 0;
this.front = 0;
}
public boolean enterQueue(int val) {
if(isFull()) {
return false;
}
this.elem[this.rear] = val;
this.rear = (this.rear + 1) % this.elem.length;
return true;
}
public boolean deleteQueue() {
if(isEmpty()) {
return false;
}
this.front = (this.front + 1) % this.elem.length;
return true;
}
//Get the element of the team head
public int Front() {
if(isEmpty()) {
return -1;
}
return this.elem[this.front];
}
//Get the element at the end of the team
public int Rear() {
if(isEmpty()) {
return -1;
}
//When rear reaches 0 subscript
int index = (this.rear == 0) ? this.elem.length - 1 : this.rear - 1;
return this.elem[index];
}
public boolean isEmpty() {
//Meet, is an empty queue
return this.front == this.rear;
}
public boolean isFull() {
return (this.rear + 1) % this.elem.length == this.front;
}
}