1, Tree
1. General
- Different from the one-to-one linear relationship represented by the linear table, the tree represents the more complex nonlinear relationship between data elements.
- Intuitively, the tree is a hierarchical structure defined by branch relationship, which is a one to many relationship
- Definition of tree: a tree is a finite set of n (n > = 0) nodes
- There is only one} root
- When n > 1, the other nodes can be divided into m (M > 0) disjoint finite sets T1, T2,..., Tm, in which each set itself is a tree and is called the subtree of the root.
The definition of tree itself is a recursive definition, that is, the concept of tree is used in the definition of tree
2. Some basic terms
- Tree node: contains a data element and several branches pointing to its subtree
- degree: the number of subtrees owned by a node
- A node with a degree of * * 0 is called a leaf * * or a * * terminal node * *. Nodes with a degree other than * * 0 * * are called non terminal nodes or branch nodes
- The root of the subtree of a node is called the child of the node, and the corresponding node is called the child's parent
- Children of the same parents are called sibling s
- The {ancestor of a node is all nodes from the root to the branch through which the node passes.
- Any node in the subtree with a node as the root is called the descendant of the node
- The {Level of a node is defined from the root. The root is the first Level, and the children of the root are the second Level, and so on
- The maximum level of nodes in a tree is called the depth or height of the tree
2, Binary tree
1. General
-
Definition: constraints are imposed on general trees:
-
Each node can have at most two subtrees, that is, there is no node with a degree greater than 2 in the binary tree
-
Subtrees can be divided into , left and right , and , left and right
-
There are 5 forms:
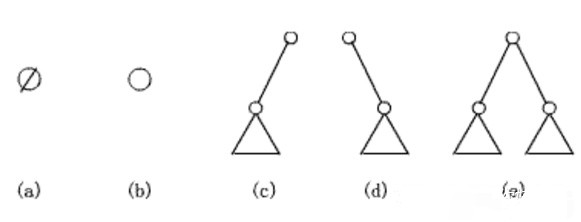
- Full binary tree and complete binary tree (delete nodes from right to left at the bottom of full binary tree)
2. Important characteristics
- The binary tree has at most ^ 2i-1 ^ nodes in the ^ I ^ layer
- A binary tree with a depth of ^ K ^ has at most ^ 2k-1 ^ nodes
- A complete binary tree with a height (or depth) of , K , has at least , 2k-2 , leaf nodes
- The number of nodes on the leaves of a non empty binary tree is equal to the number of nodes with a degree of 2 plus 1, that is, n0 = n2 + 1
n1 of a complete binary tree can only be 0 or 1
- For a binary tree with a degree of M, the node with a degree of 1 is n1, the node with a degree of 2 is n2,..., and the number of nodes with a degree of M is nm, then the number of leaf nodes: n0**= 1 + n2****+ 2n3 * * * * +... + (m-1)nm**
- A complete binary tree with n nodes, with a depth of {log2n + 1
- Numbering nature: a complete binary tree of N nodes (its depth is ^ log2n + 1), and each node is numbered from top to bottom and from left to right (1~n). Then: if i is the number of a node A:
- If i is not equal to 1, the parent node number of a is: ⌊ i/2 ⌋
- If ﹤ 2i ≤ n, the left child number of a is ﹤ 2i; If * * 2i > n * *, a * * no left child * *;
- If * * 2i + 1 ≤ n * *, the right child number of a is * * 2i + 1 * *; If * * 2i + 1 > n * *, a * * no right child * *;
3, Storage structure of binary tree
1. Sequential storage
- Use an array of {to store data elements
- From the storage point of view, this sequential storage structure is only applicable to {complete binary trees
Because in the worst case, a single tree with a depth of , K , and only , K , nodes (there are no nodes with a degree of 2 in the tree) needs a one-dimensional array with a length of , 2k-1 ,.
2. Chain storage
- Store data elements and the relationship between data elements in the form of a linked list.
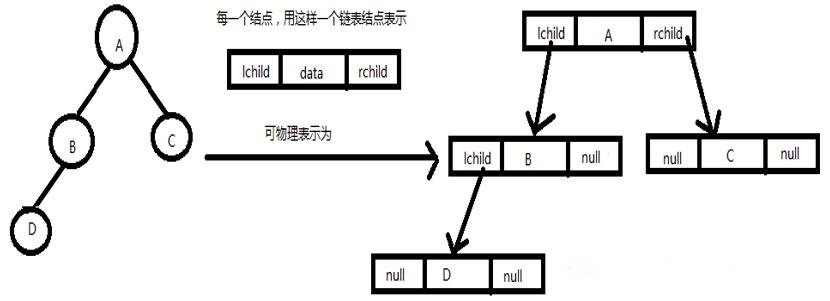
4, Traversal of binary tree
1. Determine the binary tree from the traversal sequence
- It can be determined by # pre order and middle order
- It can be determined by # post order and middle order (but note that the last post order is the root and the next is the right subtree root)
- It can be determined by {hierarchy and middle order
2. Estimate the binary tree according to the traversal sequence
- Trees with the same {traversal sequence before} and {traversal sequence after}: only root nodes
- The pre order , traverses a binary tree with the same , as the middle order , traverses: all nodes have no left subtree (right single branch tree)
- Middle order , traverses a binary tree with the same , as post order , traverses: all nodes have no right subtree (left single branch tree)
- Pre order traversal and post order traversal of a binary tree with {opposite}: no left subtree or no right subtree (only one leaf node) with a height equal to its node number
- Binary tree with traversal in the former order and traversal in the middle order: all nodes have no right subtree (left single branch tree)
- Middle order , ergodic and post order , ergodic binary trees with , opposite: all nodes have no left subtree (right single branch tree)
3. Traversal and tree building code
- Construction of binary tree
- Depth first traversal (first order, middle order and last order)
- Breadth first traversal (first order, second order)
/* BitTree.java */
package com.java.tree;
import java.util.LinkedList;
import java.util.Queue;
/**
* Created by Jaco.Young.
* 2018-06-13 18:26
*/
public class BitTree {
//Represents the root node of a tree uniquely determined by preorder and inorder
private TreeNode root;
/**
* Methods provided to external calls
* The character array pre represents the preorder traversal sequence, and mid represents the medium order traversal sequence
*/
public void build(char[] pre, char[] mid){
//Assign the root node of the created tree to root
root = buildTree(pre,0, pre.length-1, mid, 0, mid.length-1);
}
/**
* Prerequisite: there are no duplicate elements in the tree
* A method of constructing binary tree from preorder traversal sequence and middle order traversal sequence
* In the process of building a tree, we always divide the sequence into left subtree and right subtree
* lPre,rPre And lMid, rMid, respectively, indicate which part of the preorder and middle order to create a tree
*/
private TreeNode buildTree(char[] pre, int lPre, int rPre, char[] mid, int lMid, int rMid){
//In the preorder traversal sequence, find the root node of the current tree
char root = pre[lPre];
//In the middle order traversal sequence, the position in the middle order is found according to the root node in the first order
int rootIndex = getRootIndex(mid, lMid, rMid, root);
//If not found, the given parameter is abnormal
if(rootIndex == -1){
throw new IllegalArgumentException("Illegal Argument!");
}
//Calculate the number of left and right subtrees of the current tree
//Entire middle order sequence: [left subtree (lmid) root (rootindex) right subtree (rMid)]
//Left subtree [lMid,rootIndex-1]
int lNum = rootIndex - lMid; //rootIndex-1 -lMid + 1
//Right subtree [rootIndex+1,rMid]
int rNum = rMid - rootIndex; //rMid - (rootIndex + 1) + 1
//Start to build the left and right subtrees of the current root node
//First build the left subtree
TreeNode lchild; //As the root node of the left subtree
//The tree with the current node as the root has no left subtree
if(lNum == 0){
lchild = null;
}else{
//At present, the left subtree of this tree is still a tree. Recursively construct the left subtree of this tree
//Let x be the subscript of the last element of the left subtree in the current tree precedence, then: x - (lpre + 1) = lNum
//Result: x = lPre + lNum
lchild = buildTree(pre, lPre + 1, lPre+lNum, mid, lMid, rootIndex - 1);
}
//Constructing right subtree
TreeNode rchild;
if(rNum == 0){
rchild = null;
}else{
//The right subtree of the current node still contains many nodes, and its right subtree needs to be constructed recursively
rchild = buildTree(pre, lPre + lNum + 1, rPre, mid, rootIndex + 1, rMid);
}
//Construct a complete binary tree
return new TreeNode(root,lchild,rchild);
}
//In the middle order traversal sequence, the position in the middle order is found according to the root node in the first order
private int getRootIndex(char[] mid, int lMid, int rMid, char root) {
for(int i = lMid; i <= rMid; i++){
if(mid[i] == root){
return i;
}
}
return -1;
}
//Structure of each node of binary tree
private class TreeNode{
//Data stored in nodes
char item;
//Point to left child node
TreeNode lChild;
//Point to the right child node
TreeNode rChild;
//Construct method to complete initialization
public TreeNode(char item, TreeNode lChild, TreeNode rChild){
this.item = item;
this.lChild = lChild;
this.rChild = rChild;
}
}
### How to get free architecture learning materials?



> Due to space constraints, pdf The detailed information of the document is too comprehensive, and there are too many details, so only the screenshots of some knowledge points are roughly introduced. There are more detailed contents in each small node!**[If you need a program, you can poke it here and get it for free](https://codechina.csdn.net/m0_60958482/java-p7)**
-KYh3oNXv-1630126513645)]
[External chain picture transfer...(img-cvHD9DZz-1630126513646)]
> Due to space constraints, pdf The detailed information of the document is too comprehensive, and there are too many details, so only the screenshots of some knowledge points are roughly introduced. There are more detailed contents in each small node!**[If you need a program, you can poke it here and get it for free](https://codechina.csdn.net/m0_60958482/java-p7)**