1. Stack
Related concepts of stack
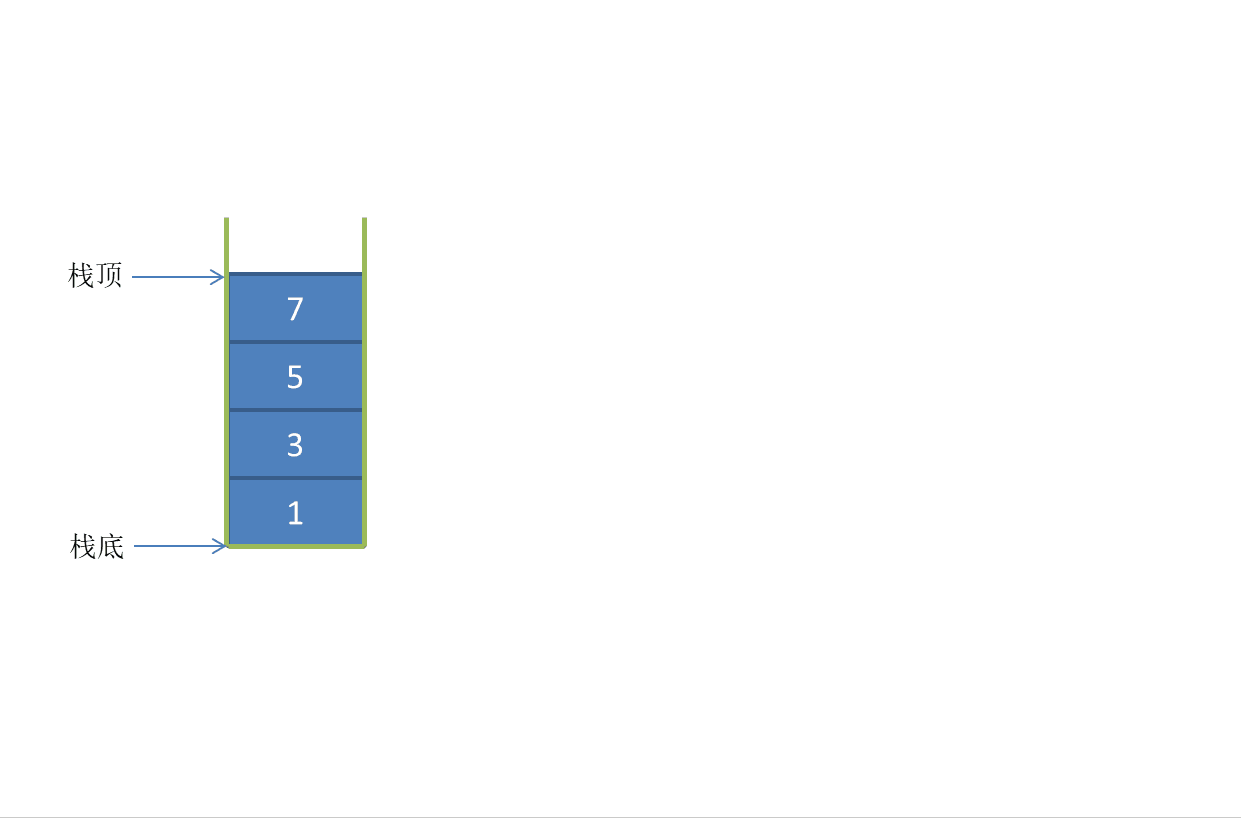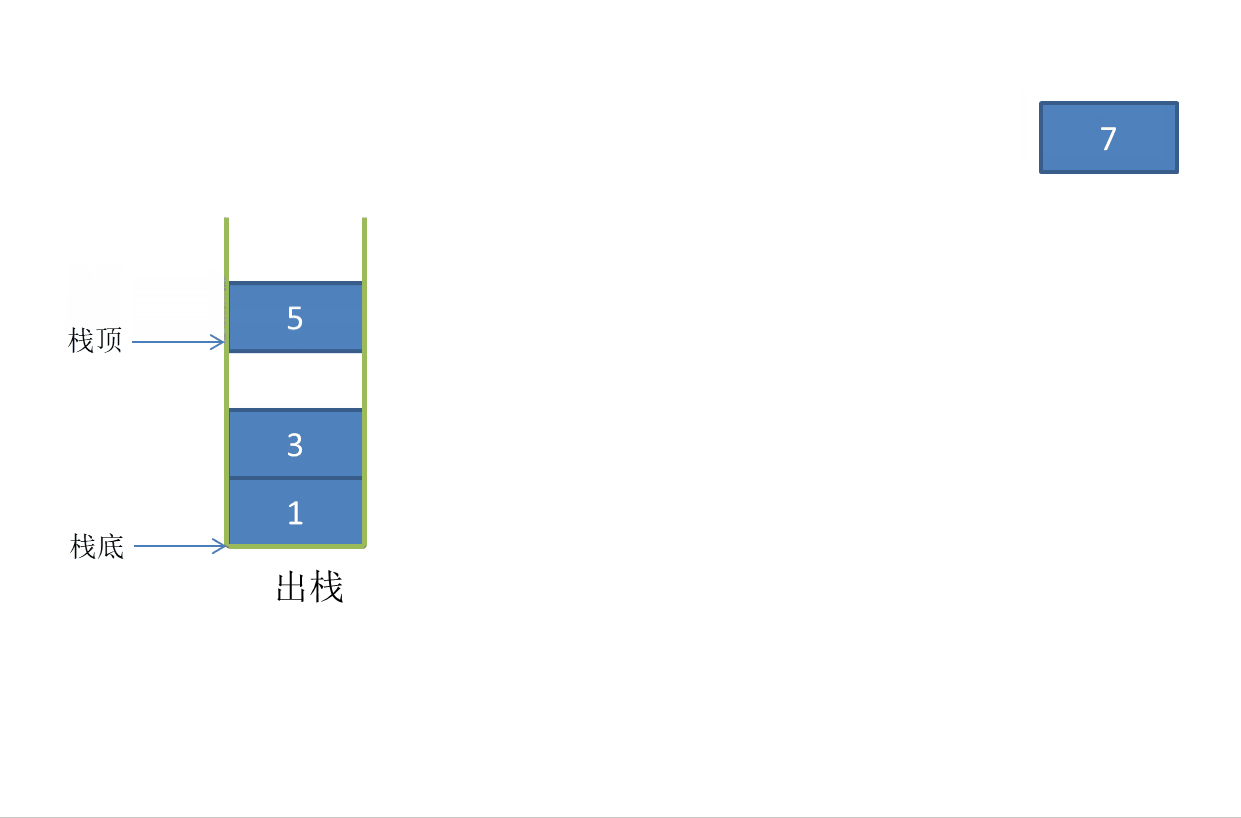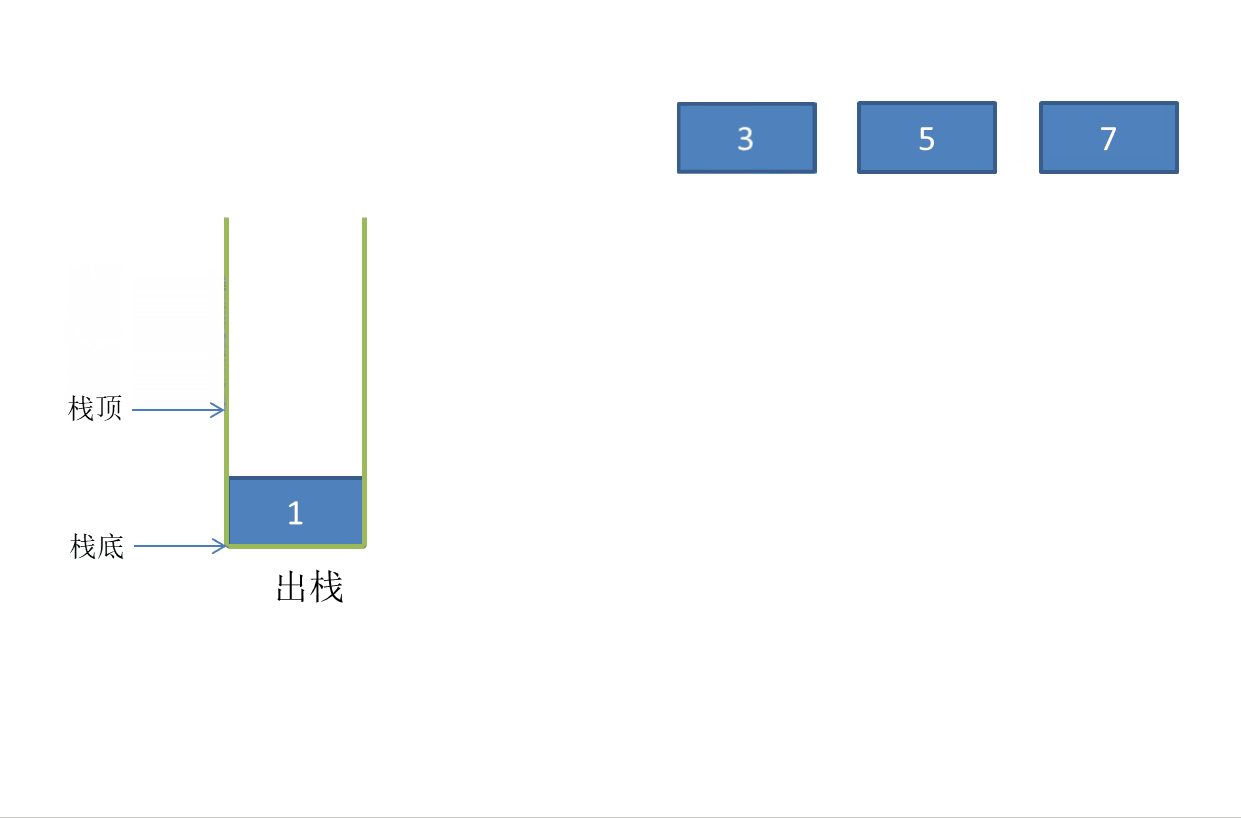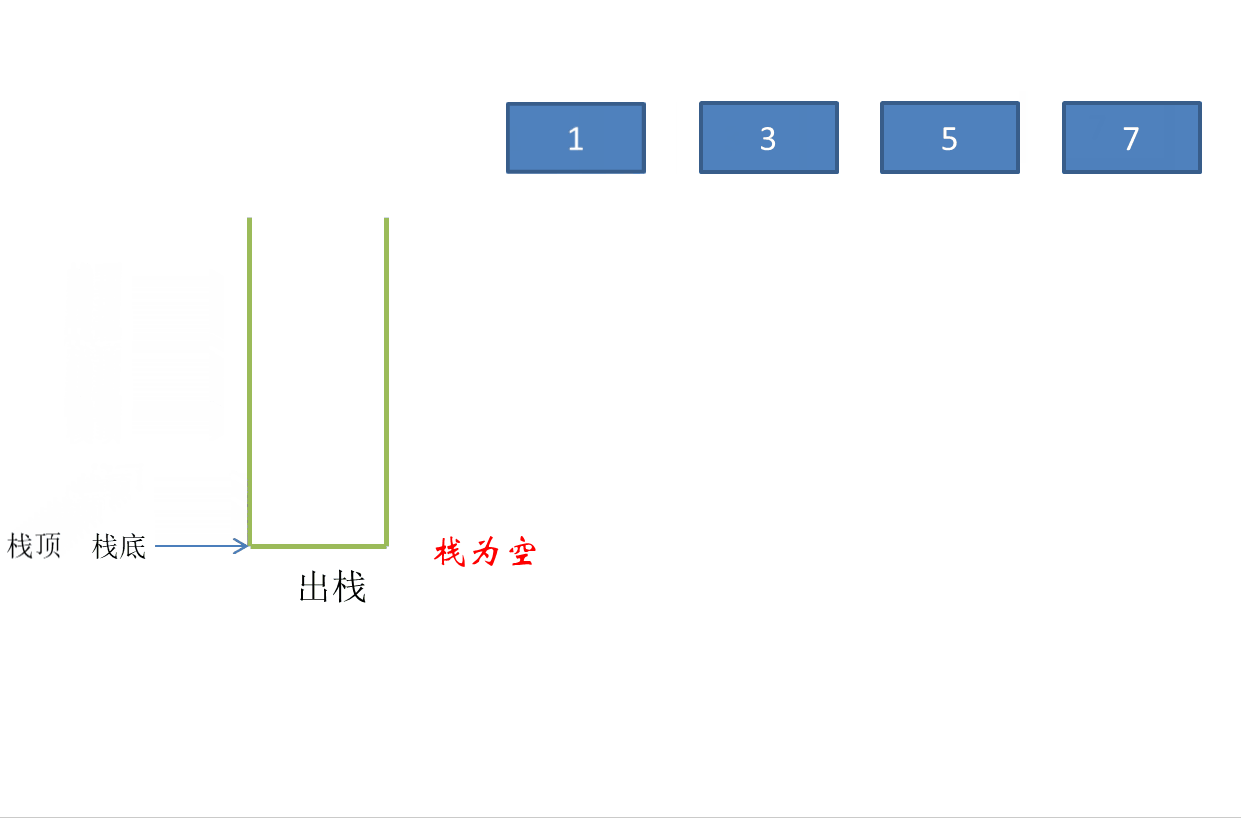
**First of all, stack is a basic and commonly used data structure. Its characteristics are: first in and last out. The bottom layer can be realized by linked list or array. When using stack as a data structure, only one end of the array can be operated** One end of the insert and delete operation is the top of the stack, and the other end is the stack
Bottom.
Stack can also be understood in this way: when you wash dishes in the kitchen, after one dish after another, the dishes are stacked one by one. The dishes washed first must be at the bottom of this pile of dishes. If we want to take the dishes, we can only take the top one of this pile of dishes. In addition, when you enter a web page, other columns are opened in this web page. Entering this web page is equivalent to entering the stack, and when we want to exit this web page, we need to close it, which is equivalent to leaving the stack.
Specific dynamic diagram for demonstration
Look at the picture and speak:
Stack:
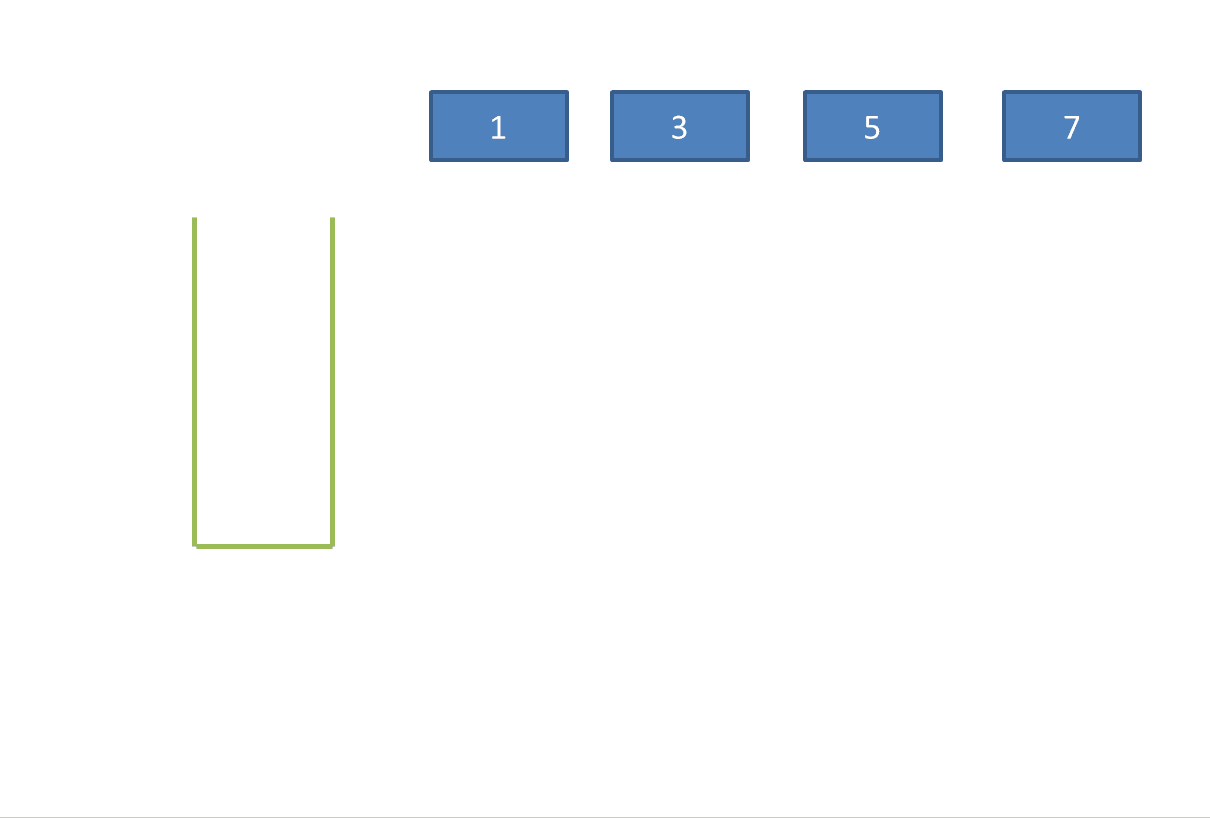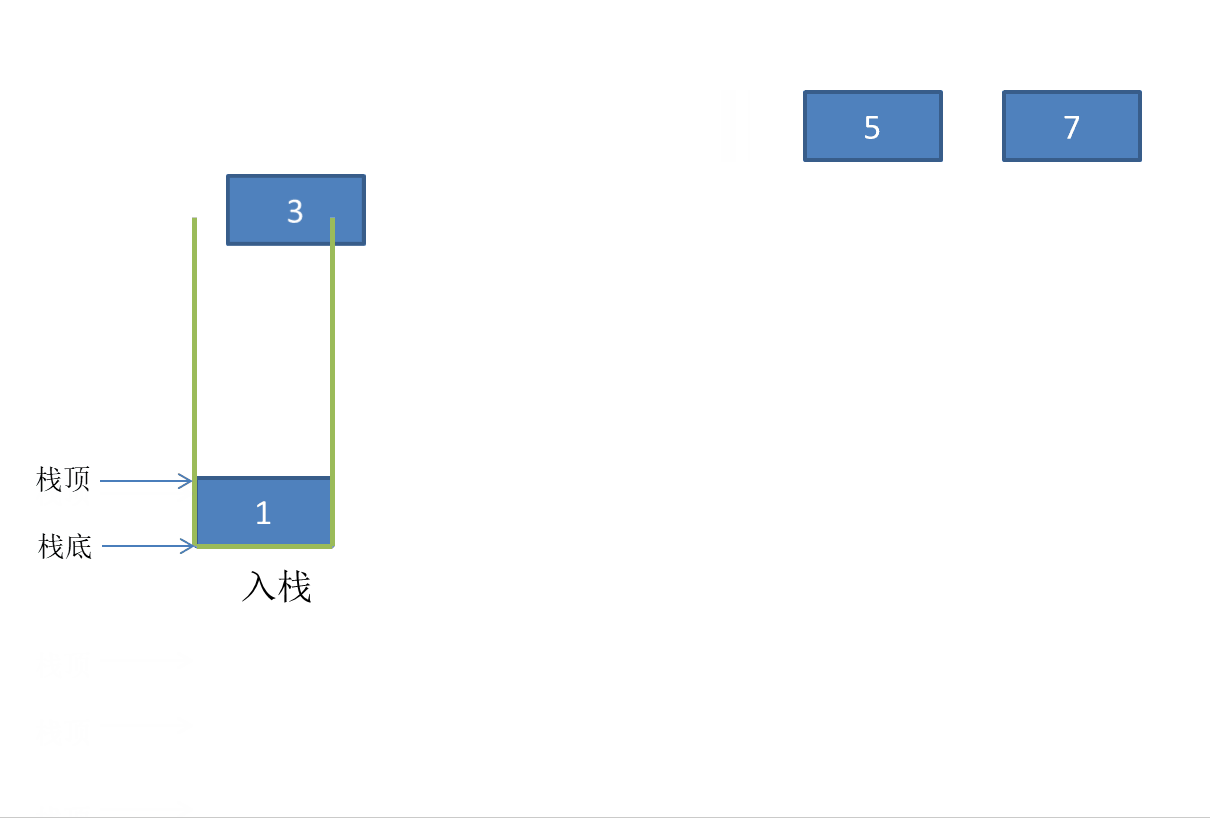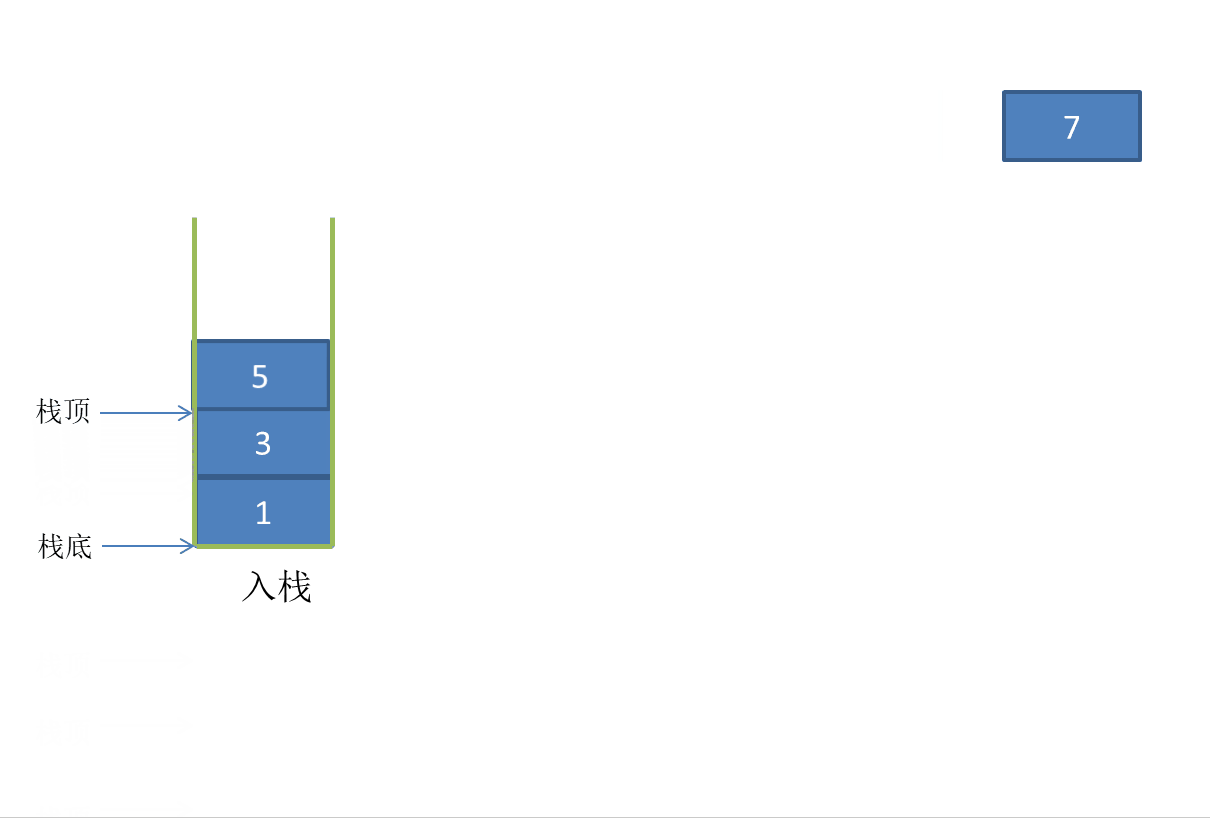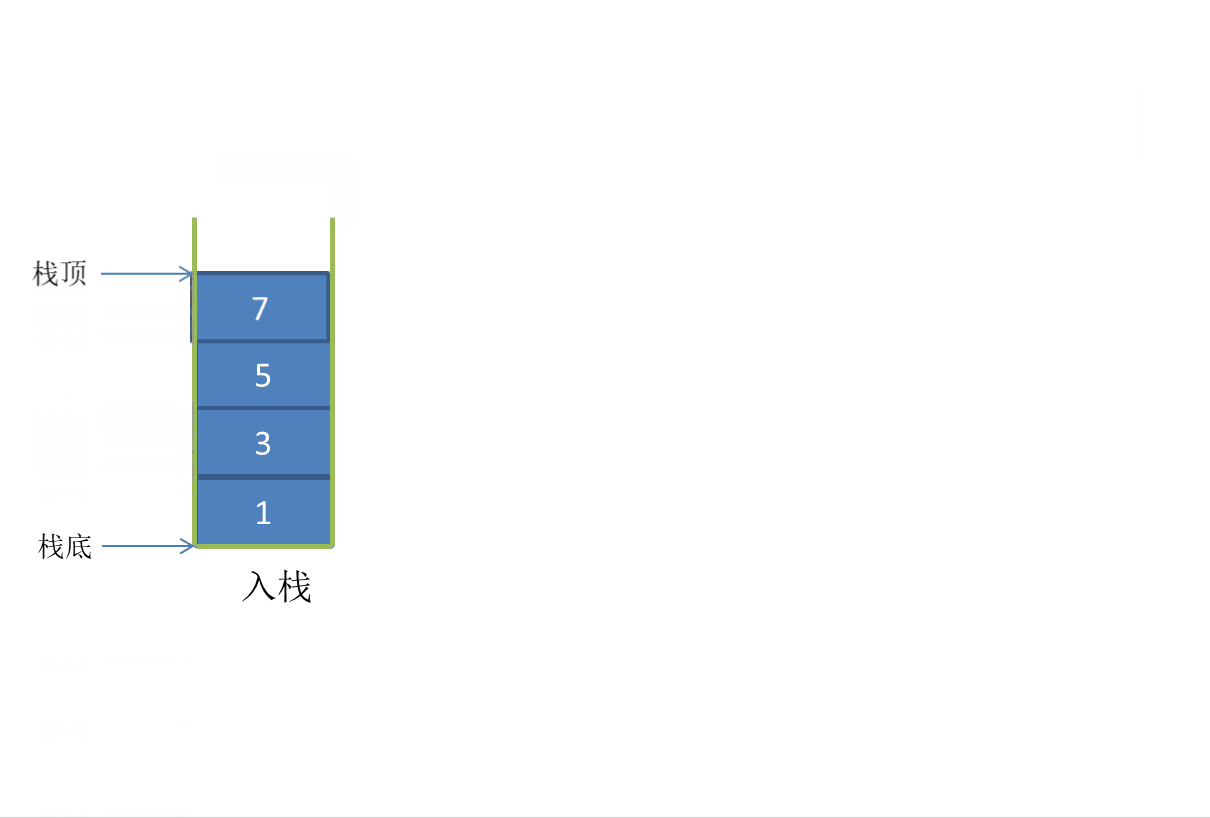
Out of stack:
Stack pressing: inserting elements into the stack, also known as stacking.
Stack out: delete the stack top element and pop up the stack top element.
Stack related methods:
First, instantiate a stack object before using the stack data structure.
Stack<Integer> stack = new Stack<>();//What is added in < > is the name of the class corresponding to adding data to the stack. If it is a basic data type, use the wrapper class.
Several common methods:
| Method name | Method interpretation |
|---|---|
| void push(int val) | Push data into the stack |
| void pop() | Delete stack top element |
| boolean empty() | Determine whether the stack is empty |
| int peek() | Return stack top element |
| int size() | Returns the number of elements in the stack |
Case:
public static void main(String[] args) {
Stack<Integer>stack = new Stack<>();
stack.push(1);
stack.push(2);
stack.push(3);
System.out.println(stack.peek());
stack.pop();
System.out.println(stack.peek());
System.out.println(stack.size());
System.out.println(stack.empty());
//Operation results:
//3
//2
//2
//false
}
Convert infix expression to suffix expression
Suffix expression: Inverse Polish (Reverse Polish notation, RPN, or inverse Polish notation), also known as suffix expression (write the operator after the operand), similar to: 2,3,5, *, +;
Infix expression: Infix expression It is a general expression method of arithmetic or logic formula. be similar to
3*5+2;
So how can we transform infix expression into suffix expression?
Here's a technique that's absolutely amazing to you!
Example: there is an infix expression a * (B - (c + D)), now you need to get its corresponding suffix expression
Solution: according to the expression, multiply and divide first and then add and subtract. If there are brackets, move the operators on the bracket surface to the corresponding brackets, and finally remove all brackets.
Problem solving process:
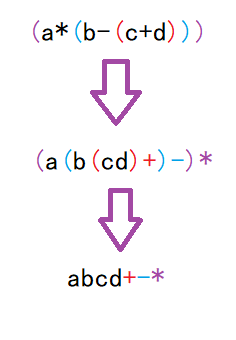
So how to convert suffix expression into infix expression?
Here we will use the stack we just learned today
Solution: traverse the suffix expression. If you traverse the string, if you traverse the numeric character, convert the numeric character into a number, and then press it into the stack. When you traverse the non numeric character, pop up the two elements in the stack. Note that the pop-up is to pop up the two elements at the top of the stack. And perform addition, subtraction, multiplication and division. The detailed thinking of the problem-solving process and related codes are listed below in the stack and queue related exercises.
Manually implement a stack (the bottom layer is array)
//Array implementation stack
//Custom exception, inheriting the expectation class
class MyException extends Exception{
public MyException(String message){
super(message);
}
}
public class MyStack {
public int []elem;
public int usedSize;//When no element is added to the array, the effective length is 0
//The length of the initial session array is 10
public MyStack() {
this.elem = new int[10];
}
//Judge whether the array is now full. If the array is full, expand the capacity
public boolean isFull(){
if(this.elem.length == usedSize){
return true;
}
return false;
}
//First judge whether the array is full. If it is full, double the capacity
public int push(int val){
//If the array is full and cannot be loaded, expand the capacity
if(isFull()){
this.elem = Arrays.copyOf(this.elem,2*this.elem.length);//Double expansion
}
this.elem[usedSize] = val;//By default, the new element is added to the end of the last element
usedSize++;//Effective length plus 1
return this.elem[usedSize];
}
public int pop()throws MyException{
//If the effective length of the array is found to be 0 during stack out, it indicates that the array is empty, and then an exception is reported
if(usedSize == 0){
//Throw exception
throw new MyException("The array is empty and cannot be deleted");
}
//Because the stack can only be pushed out from the top of the stack, the last element in the array is deleted here
int num = this.elem[usedSize - 1];
//Effective length minus one
usedSize--;
return num;
}
public int peek()throws MyException{
//If the array is empty
if(usedSize == 0){
//Throw exception
throw new MyException("The array is empty and cannot be displayed");
}
return this.elem[usedSize-1];
}
public boolean empty(){
if(usedSize == 0){
return true;
}
return false;
}
}
Manually implement a stack (the bottom layer is a single linked list)
When using a single linked list to implement a stack, you should use the end to end insertion method. Insert elements in the head node and delete elements in the head node. If you use the tail insertion method, the time complexity will rise. You should traverse backwards from the head node when inserting and deleting. Its time complexity is O(n), and if head interpolation is used, its time complexity is O(1)
//Create a node class. The data field stores the elements in the stack, and the pointer field stores the address of the next element
class Node {
public int val;
public Node next;
public Node(int val){
this.val = val;
}
}
public class MyStack1 {
public Node head = null;
public int push(int val){//Head insertion
Node node = new Node(val);
//Let the subsequent pointer of node point to head
node.next = head;
//Node updates the position of the head node before the head node
head = node;
return head.val;
}
public int pop() throws RuntimeException{
Node cur = head;//Reserved node
if(head != null){
//The head node refers to the next node of the head node
head = head.next;
}else{
//If the header node is empty, there is no data in the linked list, and an exception is thrown
throw new RuntimeException("Stack empty");
}
return cur.val;
}
public int peek() throws RuntimeException{
if(head == null){
throw new RuntimeException("Stack empty");
}
return head.val;
}
public boolean empty(){
if(head == null){
return true;
}
return false;
}
}
queue
Basic concepts about queues
Queue: its characteristic is first in, first out
Out of the team: out of the team head, that is, delete elements at the team head.
Join the team: enter from the end of the team, that is, add elements at the end of the team.
At the bottom of the queue is a two-way linked list
The queue can also be understood in this way. It is the same as us in the school canteen (we need to queue up). Those who arrive first will eat first. After dinner, they leave the queue, which is equivalent to leaving the queue. However, those who come to the team later can only line up to the end of the team, which is equivalent to joining the team.
Dynamic diagram demonstration:
Join the team:

Out of the team:
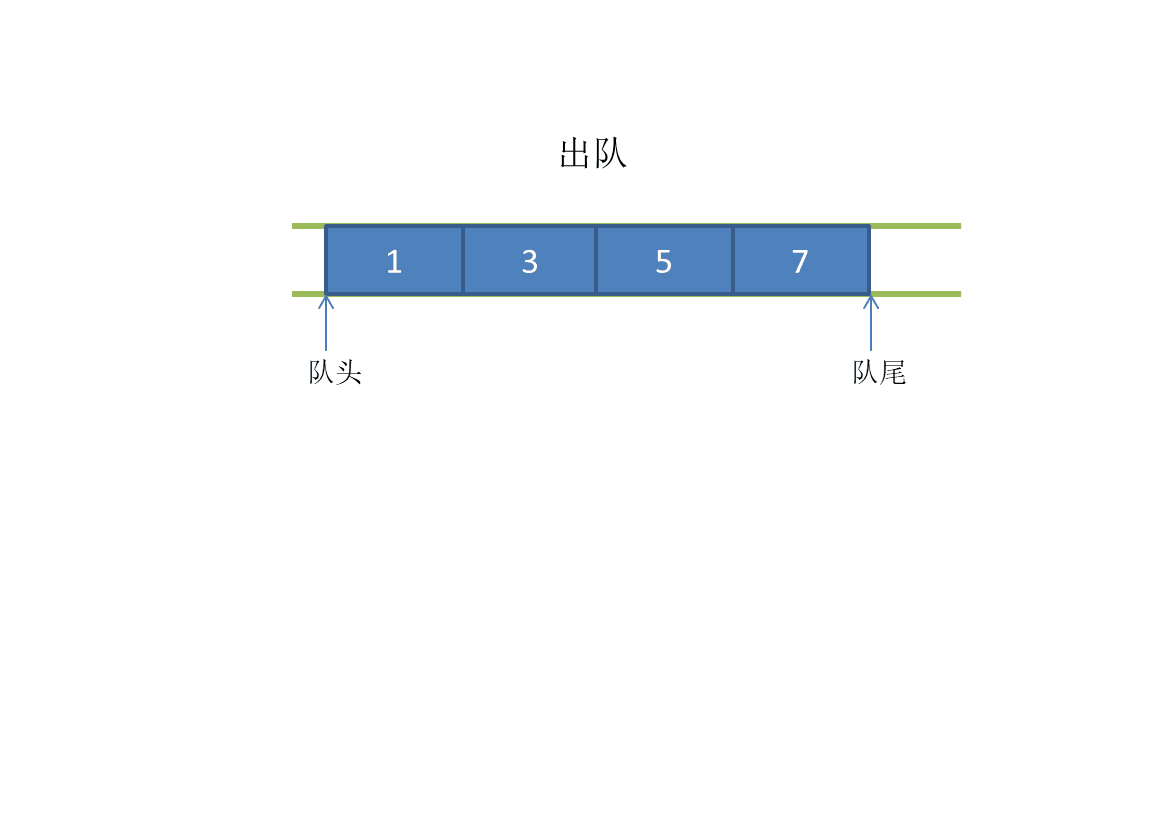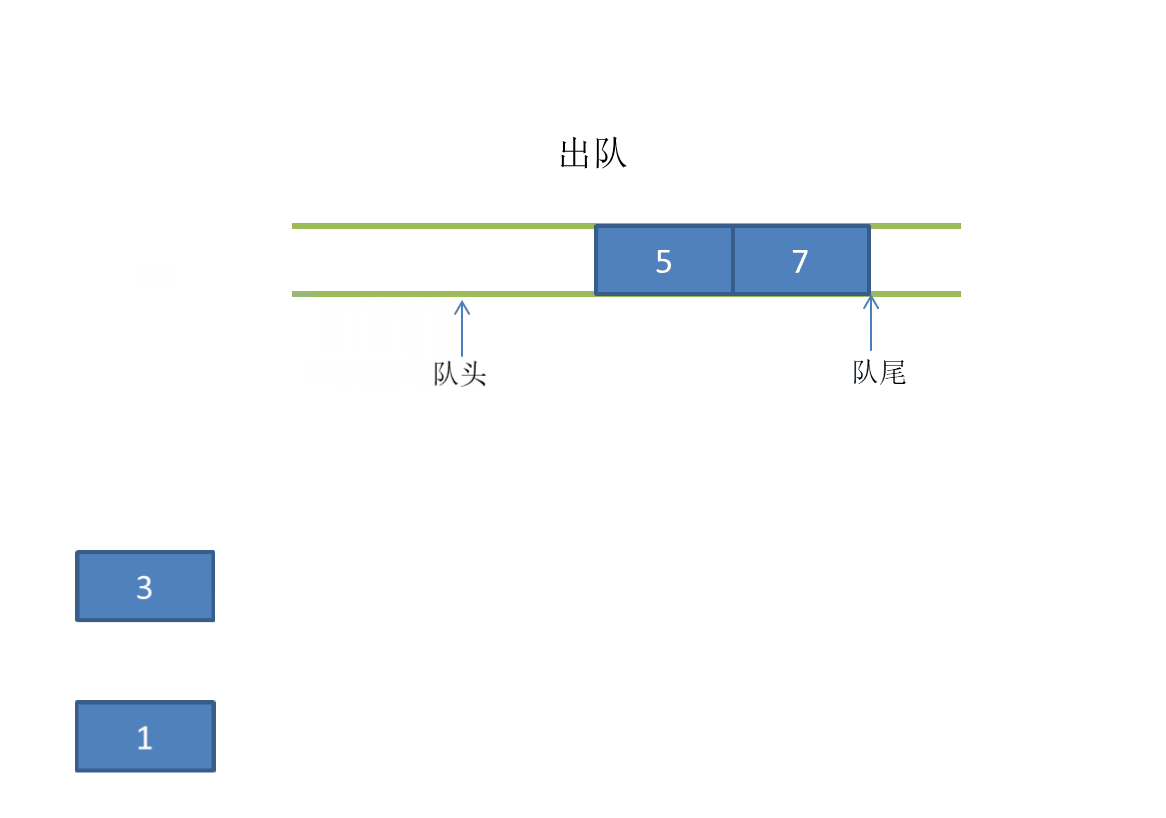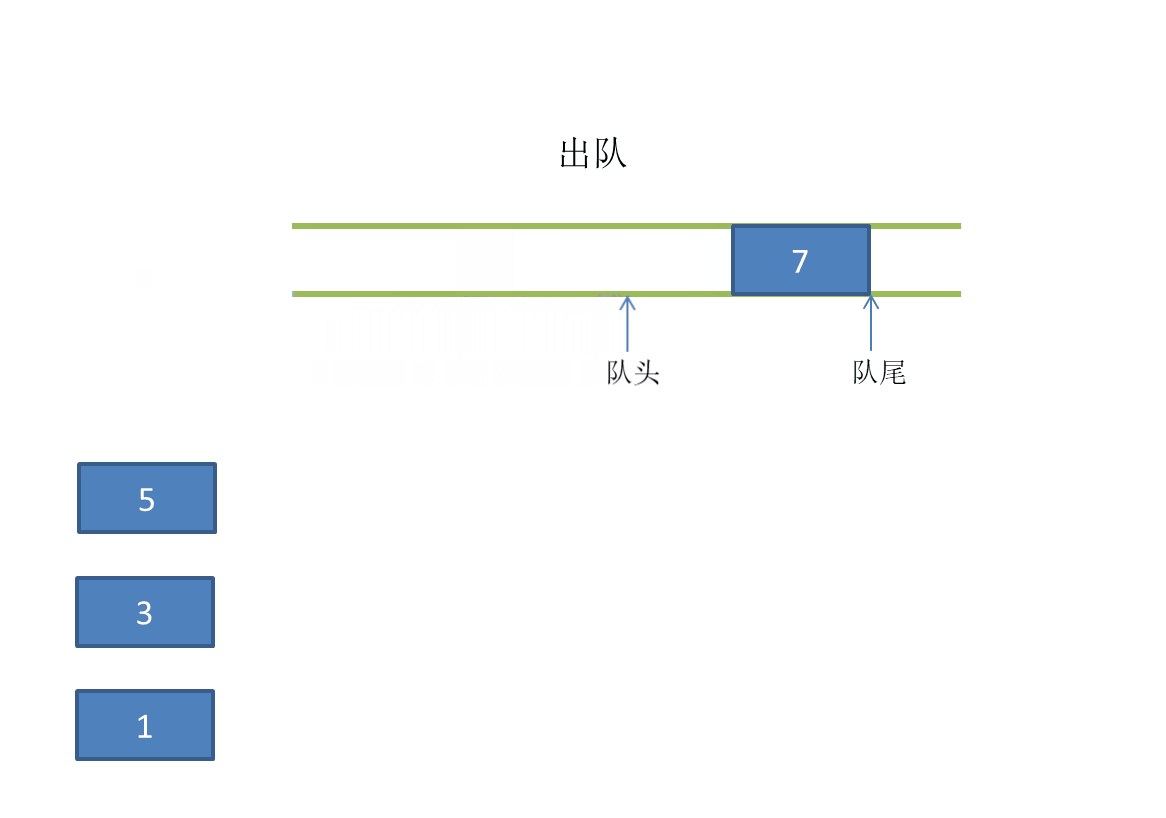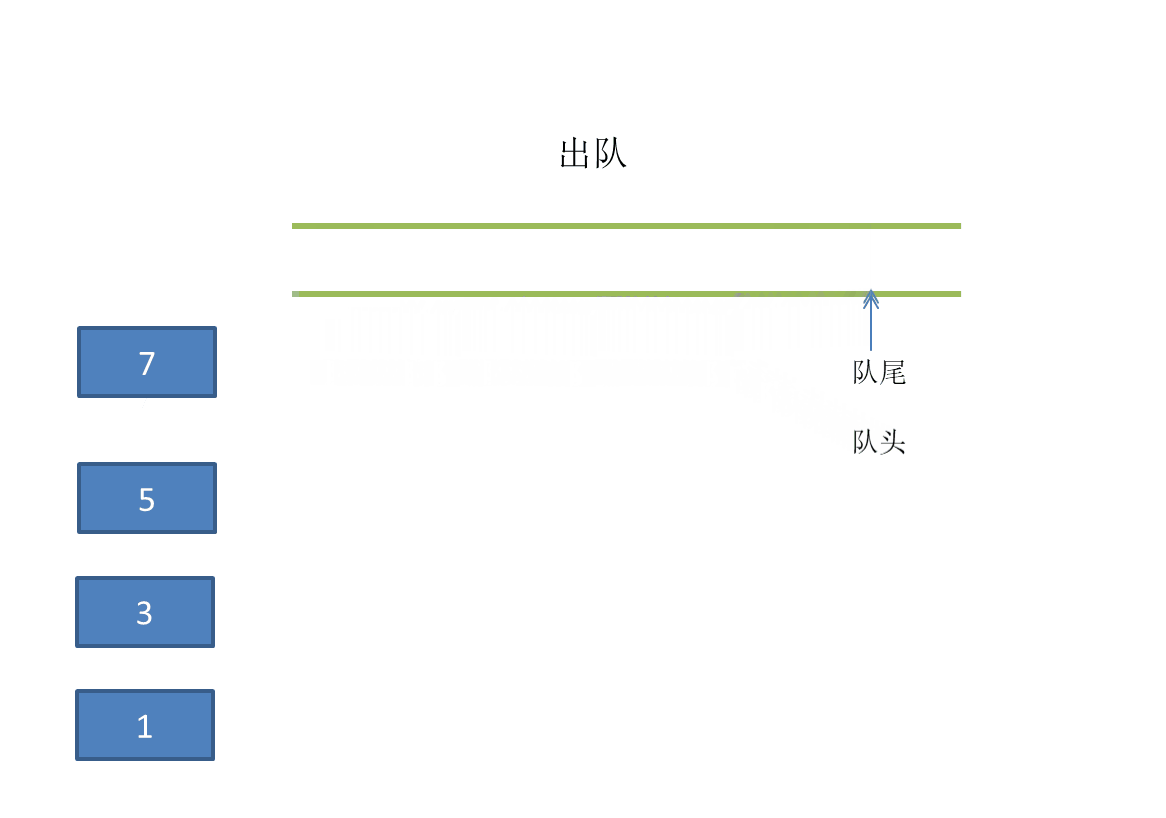
Some common methods related to queue
Before calling some common methods of the queue, first instantiate a queue object.
Queue<Integer>qurue = new LinkedList<>();
Some common methods of queue:
| Method name | Method interpretation |
|---|---|
| void offer(int val) | Queue val |
| void poll() | Out of the team, delete the team head element |
| boolean isEmpty() | Determine whether the queue is empty |
| int peek() | Returns the queue header element |
Case:
public static void main(String[] args) {
Queue<Integer> queue = new LinkedList<>();
queue.offer(1);
queue.offer(2);
queue.offer(3);
System.out.println(queue.peek());
queue.poll();
System.out.println(queue.peek());
System.out.println(queue.isEmpty());
System.out.println(queue.size());
}
//Operation results:
//1
//2
//false
//2
Manually implement a queue (the bottom layer is a single linked list)
After reading the above methods about queues, how do they implement them?
//Create a node class. In the node, the data field is the element added in the queue, and the pointer field represents the address of the next element
class Node{
public int val;
public Node next;
public Node(int val){
this.val = val;
}
}
public class MyQueueLinked {
public Node head;//Represents the header node of the linked list
public Node last;//Represents the tail node of the linked list
public int size;//Length of linked list
public void offer(int val){
//Add element to queue
Node node = new Node(val);
if(last == null){
head = node;//If the tail node is empty when joining the queue, it means that there are no elements in the queue. At this time, let the head node point to the node and the tail node point to the node
last = node;
}else{
last.next = node;//If the linked list is not empty, let the pointer of the tail node point to node
last = node; //Then update the tail node
}
size++;//Finally, add one to the number of linked list nodes
}
public int peek()throws RuntimeException{//Displays the header of the queue
//If the queue is empty
if(empty()){
throw new RuntimeException("Queue is empty");
}
//Since the queue is dequeued from the head of the queue, the val value of the head node is displayed
return head.val;
}
public int poll()throws RuntimeException{//Get out of the team. Delete the header of the queue
//If the queue is empty
if(empty()){
throw new RuntimeException("Queue is empty");
}
//Save node
Node cur = head;
//Out of the queue, update the nodes of the linked list so that the head node of the linked list becomes a node after the head node
head = head.next;
//Elements in the queue minus one
size--;
return cur.val;
}
public int size(){
return size;
}
public boolean empty(){
if(head == null){
return true;
}
return false;
}
}
Manually implement a queue (the bottom layer is a circular array)
Using a linked list can implement a stack, so can you use an array?
Answer: Yes.
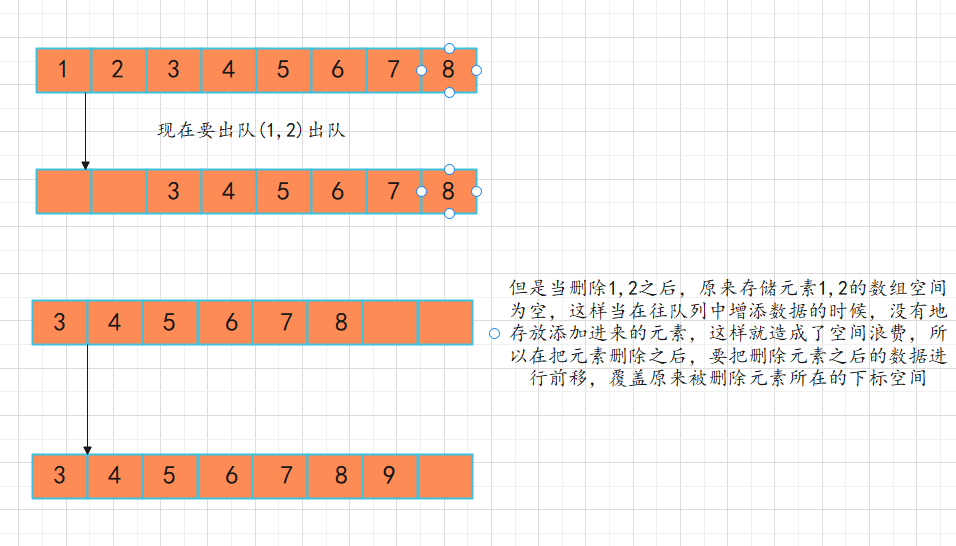
But in this way, the time complexity will be improved. Its time complexity is O(n). It's time to introduce the loop pair column.
Connect the end of the array. Form a cycle. As shown in the figure:
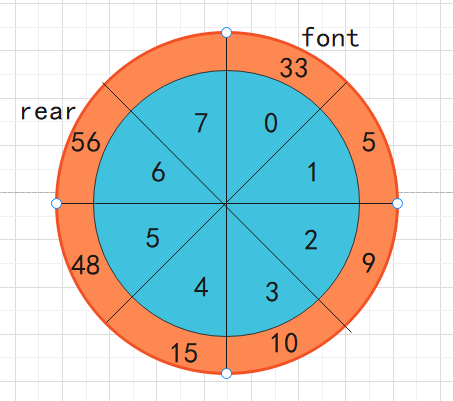
Why do we use the real subscript of a circular array and an empty element space?
Let's think about this problem first. When to judge when the circular array is full and when the queue is empty.
It's not easy for some people to think. When the real subscript and font subscript point to an element space at the same time, the array is empty, that is, the queue is empty.
But think about what to do when the data in the queue is full. Isn't that a circular array? The real subscript continues to go back. Doesn't this mean that the real subscript should coincide with the font subscript?
Think carefully about why you deliberately leave a space in the loop array.
In fact, there is a formula that can judge whether the element is full in the loop by the length of (rear + 1)% array, that is, whether the length of (rear + 1)% array is equal to font. If it is equal, it means that the array is full, and false is returned
class MyCircularQueue {
public int []elem;
public int front;//Team leader
public int rear;//Team tail
public MyCircularQueue(int k) {
this.elem = new int[k+1];//The original loop queue is initialized to 10
}
public boolean enQueue(int val) {
//Determine whether the element loop queue is full
if(isFull()){
return false;
}
this.elem[rear] = val;
int ret = this.elem[rear];
rear = (rear+1) % this.elem.length;//After adding at the end of the queue, the rear subscript moves backward
return true;
}
public boolean deQueue() {
//If the original circular queue is empty
if(isEmpty()){
return false;
}
int ret = this.elem[front];//Delete element at the head of the queue
front = ((this.front + 1) % this.elem.length);//front update
return true;
}
//Get team leader element
public int Front() {
if(isEmpty()){
return -1;
}
int ret = this.elem[front];
return ret;
}
//Get tail element
public int Rear() {
if(isEmpty()){
return -1;
}
if(this.rear == 0){
return this.elem[this.elem.length-1];
}
return this.elem[this.rear-1];
}
public boolean isEmpty() {
if(this.rear == this.front){
return true;
}
return false;
}
public boolean isFull() {
if((rear+1)%this.elem.length == front){
return true;
}
return false;
}
}
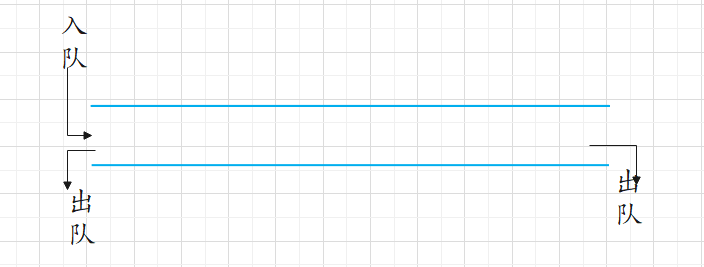
Double ended queue
Since it is a double ended queue, it is different from the queue. Its particularity is that both sides of the queue can enter and leave the queue in the double ended queue
Stack and queue related exercises
1. Bracket matching
Matching of valid parentheses OJ link
Given a string s that only includes' (',') ',' {','} ',' [','] ', judge whether the string is valid.
Valid strings must meet the following requirements: the left parenthesis must be closed with the same type of right parenthesis. The left parentheses must be closed in the correct order.
Problem solving ideas:
1. If the passed string is null, or the length of the passed string is zero, or the number of passed strings is odd (because the parentheses match each other), false is returned.
2. The second is to traverse the string. If the left bracket is traversed, put the left bracket on the stack. If the right bracket is traversed, peek() is used to return the top element of the stack. Judge whether the pop-up top element matches the traversed right bracket. If it matches, delete the top element of the stack. If it does not match, return false.
3. When the string passed is "[[[[]]" and there are obviously many left parentheses, when traversing the right parentheses, delete the left parentheses equal to the right parentheses, and there are still elements in the stack. Finally, if the stack is not empty, return false, that is, the parentheses do not match.
4. When the string passed is "{}}" and there are many right parentheses, judge whether the stack is empty when peek() is in the stack. If it is empty, return false directly
public static boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for(int i = 0;i<s.length();i++){
if(s.charAt(i) == '{' || s.charAt(i) == '[' ||s.charAt(i) == '('){
stack.push(s.charAt(i));
}else{
if(stack.empty()){
return false;
}
if(s.charAt(i) == '}' && stack.peek() == '{' ||s.charAt(i) == ']' && stack.peek() == '[' ||s.charAt(i) == ')' && stack.peek() == '('){
stack.pop();
}else{
return false;//Bracket mismatch
}
}
}
//If the stack is not empty, there are many left parentheses
if(!stack.empty()){
return false;
}
return true;
}
2. Convert suffix expression into infix expression and calculate the result
Suffix expression conversion OJ link
Valid operators include +, -,, /. Each operand can be an integer or another inverse expression.
explain:
Integer division preserves only the integer part.
The given inverse Polish expression is always valid. In other words, an expression always yields a valid value and there is no case where the divisor is 0.
Example 1:
Input: tokens = ["2", "1", "+", "3", ""]
Output: 9
Explanation: this expression is transformed into a common infix arithmetic expression: ((2 + 1) * 3) = 9
Example 2:
Input: tokens = ["4", "13", "5", "/", "+"]
Output: 6
Explanation: this expression is transformed into a common infix arithmetic expression: (4 + (13 / 5)) = 6
Problem solving ideas:
1. Exclude the boundary first. If the passed string array is null or the length of the string array is 0, return - 1
2. Traverse the string array. If a numeric string is traversed, convert the string into a number, and then press the array onto the stack. If a non numeric string is traversed, when the string is "+" or "*", two elements in the stack will pop up for addition or multiplication. After completing the calculation, press the calculated result into the stack. If you traverse to "-" or "/", note that the first element out of the stack is subtraction or divisor, and the last element out of the stack is subtracted or divisor.
3. Finally, there is only one data in the stack. Just peek() and it's over.
public static boolean isNumber(String taken){
if(!("+".equals(taken) ||"-".equals(taken) ||"*".equals(taken) ||"/".equals(taken)){
return true;
}
return false;
}
public static int evalRPN(String[] tokens) {
if(tokens == null){
return -1;
}
Stack<Integer>stack = new Stack<>();
//Traverse a String of type String. When traversing a numeric character, press the number onto the stack
for(int i = 0;i<tokens.length;i++){
String str = tokens[i];
if(isNumber(str)){//If the numeric character is traversed, the numeric character is pressed on the stack
stack.push(Integer.parseInt(str));
}else{//If you traverse to addition, subtraction, multiplication and division, then put the number out of the stack
int num2 = stack.pop();
int num1 = stack.pop();
if(str.equals("+")){
stack.push(num1 + num2);
}else if(str.equals("-")){
stack.push(num1 - num2);
}else if(str.equals("*")){
stack.push(num1 * num2);
}else if(str.equals("/")){
stack.push(num1 / num2);
}
}
}
return stack.peek();//Finally, there is only one element left in the stack
}
3. Realize the minimum stack
Implementation of minimum stack OJ link
Design a stack that supports push, pop and top operations and can retrieve the smallest element in a constant time.
push(x) -- pushes element x onto the stack. pop() -- delete the element at the top of the stack. top() -- get the stack top element. getMin() -- retrieves the smallest element in the stack.
Example: input:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[], [- 2], [0], [- 3], [], [], [], []] output: [null,null,null,null,-3,null,0,-2]
Explanation:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack. getMin(); --> Return - 3
minStack.pop();
minStack. top(); --> Return 0
minStack.getMin();
– > Return - 2
Problem solving ideas:
1. First create two stack objects, one is the ordinary stack, one is the smallest stack, and the other is the smallest stack, that is, the top element of the stack is the smallest of all the elements in the stack.
2. When push() is to be implemented, press each data into the ordinary stack. When the minimum stack is empty, press the same data into the stack together with the ordinary stack. When the minimum stack is not empty, when we want to press elements into the minimum stack, we should compare the top element of the minimum stack with the element newly pressed into the ordinary stack every time, If it is smaller than or equal to the top element of the smallest stack, it will be pressed to the smallest stack, otherwise it will not be pressed.
3. When you want to implement the pop() method, delete the top element of the ordinary stack to see whether the deleted element is the same as the top element in the smallest stack. If it is the same, delete the top element in the smallest stack.
4. When you want to implement the peek() method, you can directly return the top element of the ordinary stack.
5. When you want to implement the getMin() method, directly return the top element of the smallest stack.
class MinStack {
Stack<Integer>stack1 = new Stack<>();
Stack<Integer> minStack = new Stack<>();
//If the minimum stack is empty, add the same data as the original stack. If it is not empty, compare it with the element added to the minimum stack last time, and add it to the minimum stack if it is small
public void push(int val) {
stack1.push(val);
if(minStack.empty()){
minStack.push(stack1.push(val));
}else{
//Compared with the last time
if(stack1.push(val) <= minStack.peek()){
minStack.push(val);
}
}
}
public void pop() {
stack1.pop();
if(stack1.pop().equals(minStack.peek())){
minStack.pop();
}
}
public int top() {
return stack1.peek();
}
public int getMin() {
return minStack.peek();
}
}
4. Two stacks implement one queue
Two stacks implement one queue OJ link
Please use only two stacks to implement the first in first out queue. The queue should support all operations supported by the general queue (push, pop, peek, empty):
Implement MyQueue class:
void push(int x) pushes element X to the end of the queue. int pop() removes it from the beginning of the queue and returns element int peek()
Return the element boolean empty() at the beginning of the queue. If the queue is empty, return true; Otherwise, false is returned
Problem solving ideas:
1. First, create two stacks stack1 and stack2. When there is no data in the two stacks, add data in stack1z by default, which implements push().
2. When stack2 is empty, press all the data in stack1 into stack2, which reverses the order of the elements in stack1. In this way, the queue is out when the stack is out.
Dynamic diagram analysis:
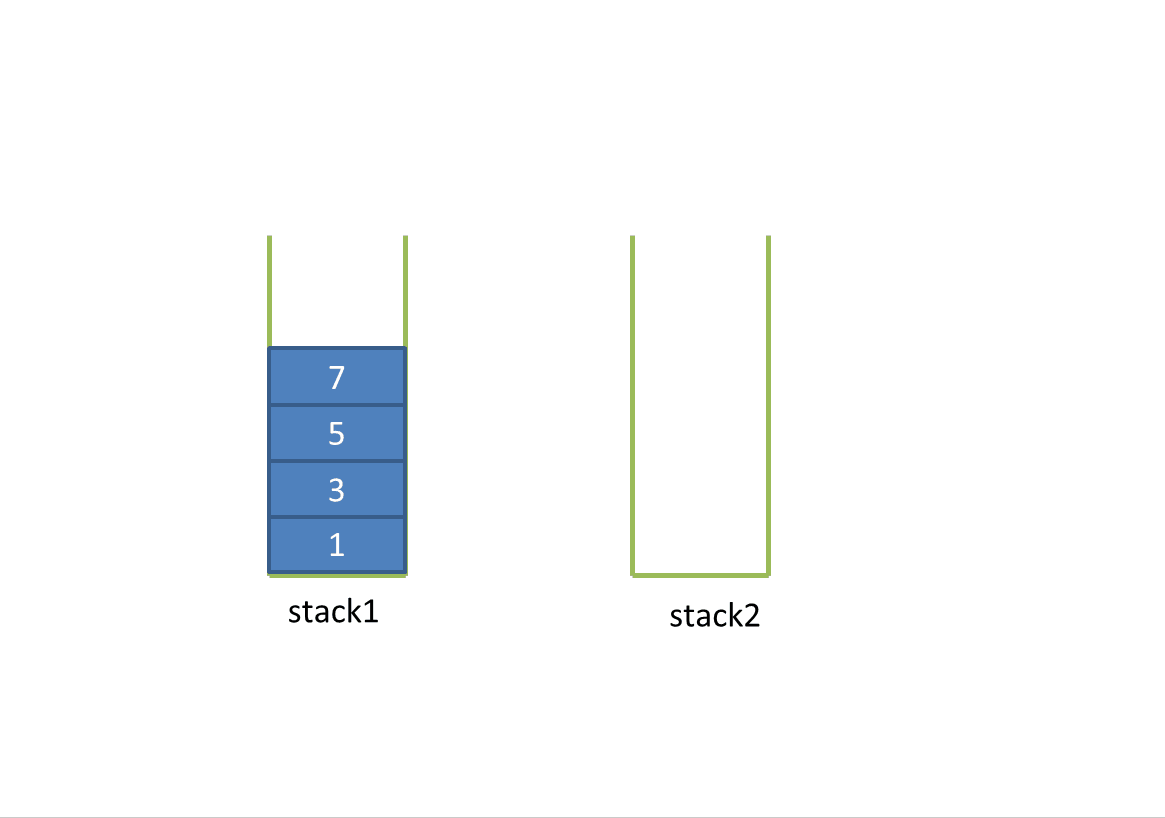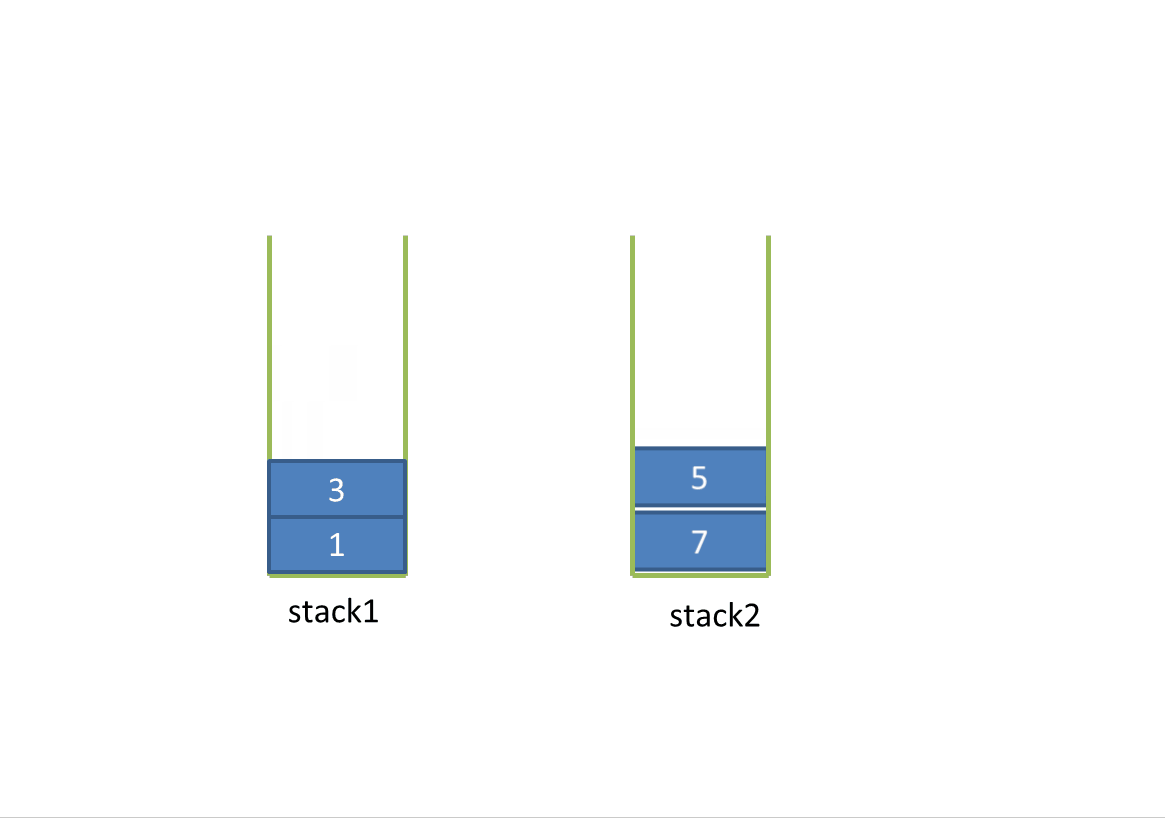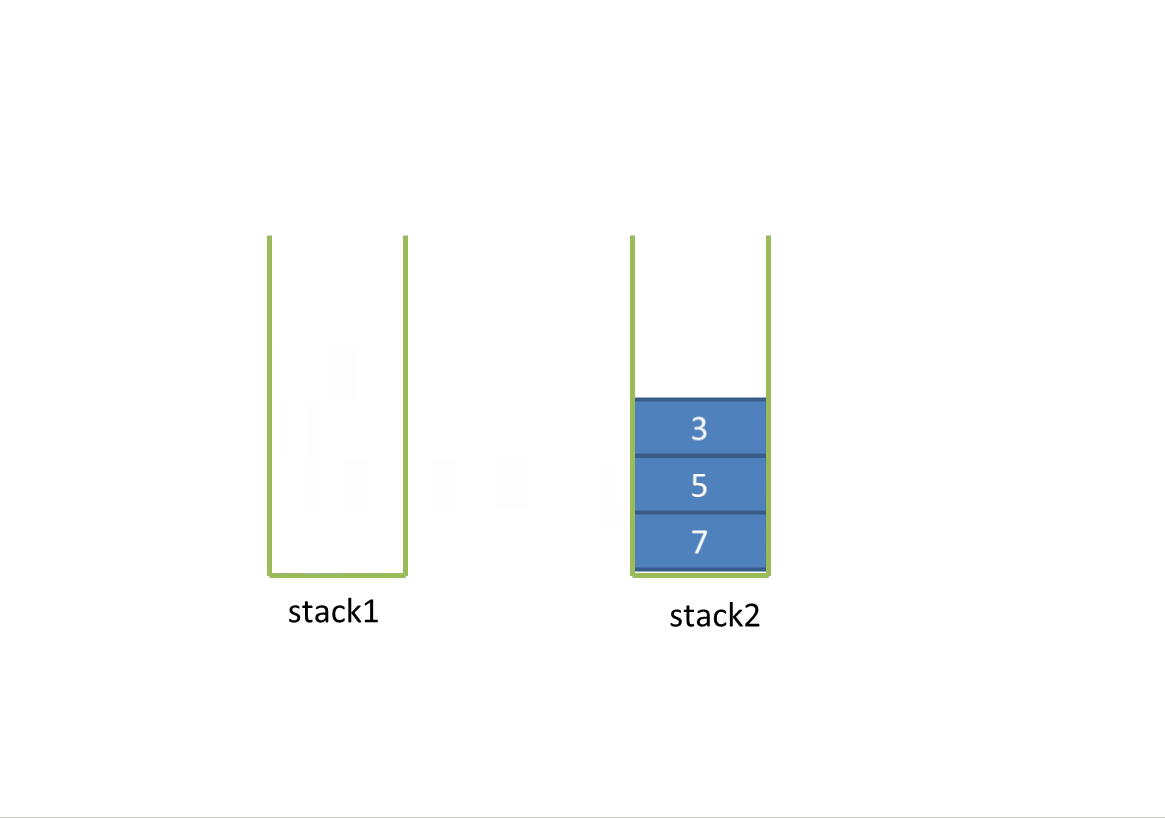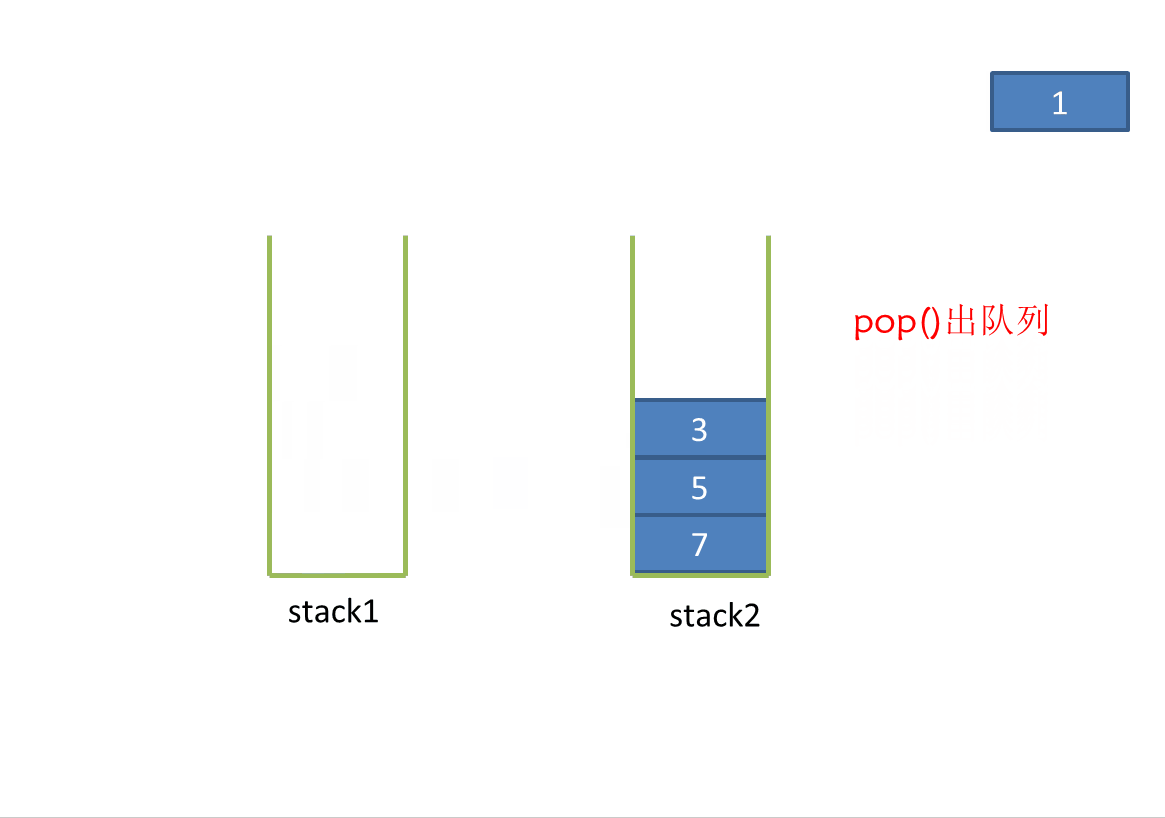
3. To implement the peek() method, directly return the stack top element in stack2.
4. To implement the empty() method, when both stacks are empty, the queue is empty
class MyQueue {
Stack<Integer>stack1 = new Stack<>();
Stack<Integer>stack2 = new Stack<>();
public void push(int x) {
stack1.push(x);
}
public int pop() {
if(empty()){
return -1;
}
if(stack2.empty()){
while(!stack1.empty()){
stack2.push(stack1.pop());
}
}
return stack2.pop();
}
public int peek() {
if(empty()){
return -1;
}
if(stack2.empty()){
while(!stack1.empty()){
stack2.push(stack1.pop());
}
}
return stack2.peek();
}
public boolean empty() {
return stack1.empty() && stack2.empty();
}
}
5. Two queues implement one stack
Two queues implement a stack OJ link
Please use only two queues to implement a last in first out (LIFO) stack, and support all four operations of the ordinary stack (push, top, pop and empty).
Implement MyStack class:
void push(int x) pushes element X to the top of the stack. int pop() removes and returns the top of stack element. int top() returns the stack top element.
boolean empty() returns true if the stack is empty; Otherwise, false is returned.
be careful:
You can only use the basic operations of the queue -- that is, push to back, peek/pop from front, size and is empty
These operations. Your language may not support queues. You can use list or deque to simulate a queue,
As long as it is a standard queue operation.
1. When deleting, move the size-1 element in one queue to another queue, and the remaining element is the element to be deleted
2. When we get the top of the stack, it is peek, which is to get the elements to be deleted, move all the elements in one queue to another queue, and mark the last element
3. When adding elements, if both queues are empty, all elements will be added to queue1 by default. If one queue is not empty, elements will be added to this queue
4. Judge whether the stack is empty. If both queues are empty, the stack is empty
class MyStack {
Queue<Integer> queue1 = new LinkedList<>();
Queue<Integer> queue2 = new LinkedList<>();
//add to
public void push(int x) {
//When adding data for the first time, because both queues are empty, data is added in queue1 by default for the first time. When adding data later, data is added in
//Add to a queue that is not empty
if(queue1.isEmpty() && queue2.isEmpty()){
queue1.offer(x);
}else{
//Not the first time
if(!queue1.isEmpty()){
queue1.offer(x);
return;
}
queue2.offer(x);
return;
}
}
//Delete stack top element
public int pop() {
//Delete the top element of the stack. In the queue that is not empty, add size-1 data to the empty queue. The remaining element is the element to be deleted
if(empty()){
return -1;
}
int e = 0;
if(!queue1.isEmpty()){
int size = queue1.size();
for(int i = 0;i<size-1;i++){
e = queue1.poll();
queue2.offer(e);
}
e = queue1.poll();
}else{
int size = queue2.size();
for(int i = 0;i<size-1;i++){
e = queue2.poll();
queue1.offer(e);
}
e = queue2.poll();
}
return e;
}
//Get the stack top element without deleting it
//Move the non empty queue to the empty queue and record the last element
public int top() {
if(empty()){
return -1;
}
int e = 0;
if(!queue1.isEmpty()){
int size = queue1.size();
for(int i = 0;i<size;i++){
e = queue1.poll();
queue2.offer(e);
}
}else{
int size = queue2.size();
for(int i = 0;i<size;i++){
e = queue2.poll();
queue1.offer(e);
}
}
return e;
}
//Determine whether the stack is empty
public boolean empty() {
if(queue1.isEmpty() && queue2.isEmpty()){
return true;
}else{
return false;
}
}
}
6. Baseball game
baseball game OJ link
You are now the recorder of a baseball game with a special game system. This game consists of several rounds. The scores in the past few rounds may affect the scores in the next few rounds.
At the beginning of the game, the record was blank. You will get a string list of recorded operations ops, where ops[i] is the ith operation you need to record. ops follows the following rules:
Integer x - indicates the new score x obtained in this round
"+" - indicates that the new score obtained in this round is the sum of the previous two scores. The title data ensures that there are always two valid scores in front of this operation.
"D" - indicates that the score newly obtained in this round is twice that of the previous round. The title data ensures that there is always a valid score in front of this operation.
"C" - indicates that the previous score is invalid and will be removed from the record. The title data ensures that there is always a valid score in front of this operation.
Please return the sum of all scores in the record.
Problem solving ideas:
- The idea of solving this problem: when traversing the string, first exclude the boundary conditions. If the string is empty or the length of the string is 0, directly return - 1
- . Traverse the string. When encountering digital characters, use the stack data structure to convert digital characters into numbers and press them into the stack.
- When the 'C' character is traversed, the top element of the stack is deleted.
- . When the'D 'character is traversed, a value is pushed into the stack, which is equal to twice the top element of the stack
- When traversing the '+' character, add up the top element of the stack and the next element of the top element in the stack, and then press it into the stack.
- Then add all the elements in the stack
class Solution {
public boolean isNumber(String str){
return !(str.equals("+")) && !(str.equals("D")) && !(str.equals("C"));
}
public int calPoints(String[] ops) {
//Exclude boundary conditions
if(ops == null || ops.length == 0){
return -1;
}
int prevC = 0;
Stack<Integer> stack = new Stack<>();
for(int i = 0;i<ops.length;i++){
String str = ops[i];
if(isNumber(str)){
stack.push(Integer.parseInt(str));
}else{
switch (str){
//Indicates that the new score obtained in this round is the sum of the previous two scores
case "+"://stack.push(prevC + stack.peek());
int num1 = stack.peek();
int num2 = stack.pop();
int num3 = stack.peek(); //Find the element below the top element of the stack
stack.push(num2);
stack.push(num1 + num3);
continue;
case "C":stack.pop();
continue;
case "D":stack.push(stack.peek() * 2);
}
}
}
int sum = 0;
while(!stack.empty()){
sum += stack.pop();
}
return sum;
}
}
7. Stack push in and pop-up sequence
Enter two integer sequences. The first sequence represents the push in order of the stack. Please judge whether the second sequence may be the pop-up order of the stack. Assume that all the numbers pushed into the stack are not equal. For example, sequence 1,2,3,4,5 is the pressing sequence of a stack, and sequence 4,5,3,2,1 is a pop-up sequence corresponding to the pressing sequence, but 4,3,5,1,2 cannot be the pop-up sequence of the pressing sequence.
- 0<=pushV.length == popV.length <=1000
- -1000<=pushV[i]<=1000
- All numbers of pushV are different
Example 1 input: [1,2,3,4,5], [4,5,3,2,1] return value: true description: the sequence [4,5,3,2,1] can be obtained in the order of push (1) = > push (2) = > push (3) = > push (4) = > pop () = > push (5) = > Pop () = > pop () = > pop () = > pop () = > pop () = > return true
Problem solving idea: put the data in the array pushA on the stack one by one. After each element is put on the stack, peek(). If it is the same as the element in the array popA, put the top element of the stack out. Finally, if the stack is empty, it shows that popA and pushA are a pair of push in and pop-up sequences
import java.util.ArrayList;
import java.util.Stack;public class Solution {
public boolean IsPopOrder(int [] pushA,int [] popA) {
Stack<Integer>stack = new Stack<>();
//When entering the stack, traverse the out of stack array. If it is equal, it will exit the simulation stack. If it is not equal, it will continue to enter the stack
int j = 0;
for(int i = 0;i<pushA.length;i++){
stack.push(pushA[i]);
while(!stack.empty() && stack.peek() == popA[j]){
stack.pop();
j++;
}
}
return stack.empty();//Returns true if the stack is empty
}
}
8. Compare strings with backspace
Given the two strings s and t, when they are input into the blank text editor respectively, please judge whether they are equal# Represents a backspace character.
If equal, return true; Otherwise, false is returned.
Note: if you enter a backspace character for empty text, the text continues to be empty.
Example 1:
Input: S = "ab#c", t = "ad#c" output: true explanation: both s and T will become "ac".
Problem solving ideas:
- The backspace here is that when you enter a character, if you press backspace, the character will be deleted. Here, the stack is used. When deleting, the pop method is used
- When traversing a string, if an alphabetic character is encountered, the alphabetic character is pressed onto the stack. If it is traversed to '#', '#' cannot be put on the stack, and the top element of the stack should be deleted.
- Finally, compare the number of elements in the two stacks. If they are not equal, then directly false. If they are equal, continue to compare whether each character in the stack is equal
- Note: when the stack is empty and traverses' # ', the elements in the stack will not be deleted
class Solution {
public boolean backspaceCompare(String s, String t) {
if(s == null && t == null){ //If both strings are empty
return true;
}
if(s == null || t == null){//If a string is empty
return false;
}
Stack<Character>stack1 = new Stack<>();
Stack<Character>stack2 = new Stack<>();
for(int i = 0;i<s.length();i++){
char ch = s.charAt(i);
if(ch == '#' && ! stack1. Empty()) {/ / when the stack is empty, the elements in the stack cannot be deleted
stack1.pop();
}
if(ch != '#'){
stack1.push(ch);
}
}
int size1 = stack1.size();
for(int i = 0;i<t.length();i++){
char ch = t.charAt(i);
if(ch == '#' && !stack2.empty()){
stack2.pop();
}
if(ch != '#'){
stack2.push(ch);
}
}
int size2 = stack2.size();
if(size1 == 0 && size2 == 0){
return true;
}
if(size1 != size2){
return false;
}
while(size1 != 0){
if(stack1.pop() != stack2.pop()){
return false;
}
size1--;
}
return true;
}
}
9. Cat and dog shelter
Given a stack and an operation sequence int [] [2] ope (vector < vector > in C + +), it represents the stack in and stack out operations. If the first element is 1, it will be put on the stack, and the second element is the sign of number; If the first element is 2, it will be out of the stack. If the second element is 0, it will be the first number to be in the stack. If it is 1, it will be the first positive number to be in the stack. If it is - 1, it will be the first negative number to be in the stack. Please return the sequence out of the stack in order, do exception handling, and ignore the error operation.
Test example: [1,1], [1, - 1], [2,0], [2, - 1]] return: [1, - 1]
Problem solving ideas:
- Solution to this problem: in the problem, it is told that the key point is that when the first element of the two-dimensional array is 2, it is out of the stack. When the second element is - 1, it is the negative number that is first put into the stack. According to the characteristics of the stack, the stack cannot be used to solve this problem, because the characteristics of the stack are that it can only be deleted and added from one end of the array. Considering the queue, the queue can not be used, Because the queue is added at one end of the array and deleted at the other end, it cannot traverse the middle elements of the array. Because you want to traverse the middle elements of the array, you can think of a list.
- If the first element in the traversed two-dimensional array is 1, perform the add operation and add the corresponding second element to the list
- If the first element is not 1, when the second element is 0, return the first element in the list and add the first element in the list to ret
- If the first element is not 1, when the second element is 1, return the first positive number from subscript 0 in the list, and add this positive number to ret
- If the first element is not 1, when the second element is - 1, it returns the first negative number in the list from the subscript 0 to see if it is, and adds this negative number to ret
import java.util.*;
public class CatDogAsylum {
public static ArrayList<Integer> asylum(int[][] ope) {
//Exclude boundary conditions
if (ope == null) {
return null;
}
ArrayList<Integer> list = new ArrayList<>();
ArrayList<Integer> re = new ArrayList<>();
for(int i = 0;i<ope.length;i++){
if(ope[i][0] == 1){
list1.add(ope[i][1]);
}else{
if(ope[i][1] == 0) {
list.add(list1.get(0));
list1.remove(0);
}else if(ope[i][1] == 1){
//Delete the first integer from the previous list in the list
for(int j = 0;j<list1.size();j++){
if(list1.get(j) * -1 < 0){
list.add(list1.get(j));
list1.remove(j);
break;
}
}
}else{
for(int j = 0;j<list1.size();j++){
if(list1.get(j) * -1 > 0){
list.add(list1.get(j));
list1.remove(j);
break;
}
}
}
}
}
return list;
}
}