1.1 INTRODUCTION
- HashMap is implemented based on the Map interface of hash table. It exists in the form of key value storage, that is, it is mainly used to store key value pairs. The implementation of HashMap is not synchronous, which means that it is not thread safe. Its key and value can be null. In addition, the mappings in HashMap are not ordered.
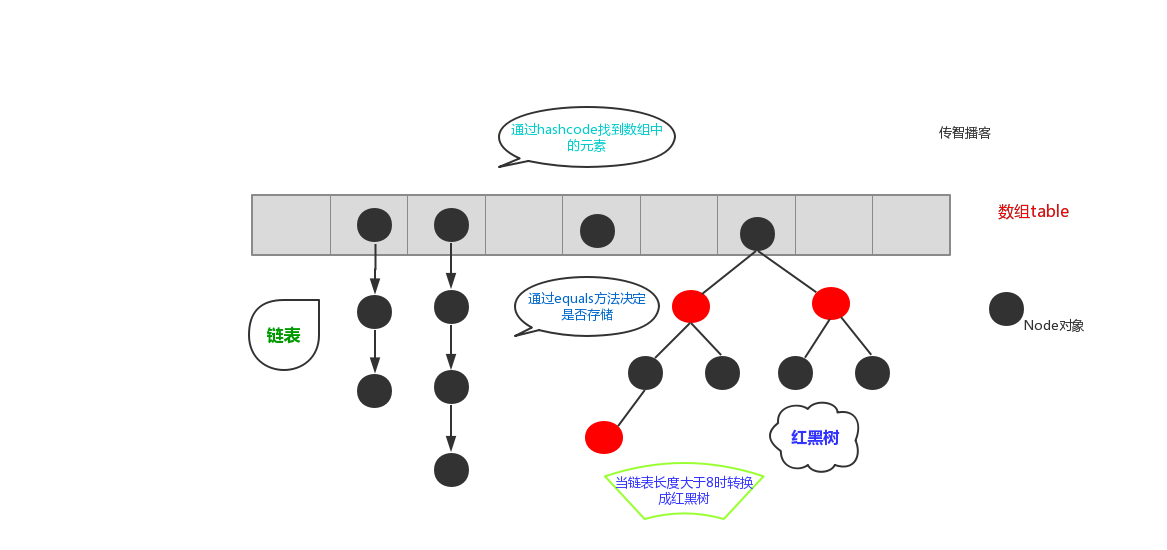
- Before JDK1.8, HashMap was composed of array and linked list. The array is the main body of HashMap, and the linked list mainly exists to solve hash conflicts (the hash code values calculated by the hashCode method called by the two objects are the same, resulting in the same array index values calculated) (the "zipper method" solves conflicts). After JDK1.8, there have been great changes in solving hash conflicts, When the length of the linked list is greater than the threshold (or the boundary value of the red black tree, which is 8 by default) and the length of the current array is greater than 64, all data at this index position will be stored in the red black tree instead.
- Before converting the linked list into a red black tree, it will be judged that even if the threshold is greater than 8, but the array length is less than 64, the linked list will not become a red black tree. Instead, you choose to expand the array.
The purpose of this is to avoid the red black tree structure as much as possible because the array is relatively small. In this case, changing to the red black tree structure will reduce the efficiency, because the red black tree needs left-hand rotation, right-hand rotation and color change to maintain balance. At the same time, when the array length is less than 64, the search time is relatively faster. To sum up, in order to improve performance and reduce search time, the linked list is converted to a red black tree when the threshold is greater than 8 and the array length is greater than 64. For details, please refer to treeifyBin method.
Of course, although the red black tree is added as the underlying data structure, the structure becomes complex, but when the threshold is greater than 8 and the array length is greater than 64, the efficiency becomes more efficient when the linked list is converted to red black tree.
1.2 features
- Access disordered
- Both key and value positions can be null, but the key position can only be null
- The key position is unique, and the underlying data structure controls the key position
- The data structure before jdk1.8 is: linked list + array jdk1.8 is followed by: linked list + array + red black tree
- Only when the threshold (boundary value) > 8 and the array length is greater than 64 can the linked list be converted into a red black tree. The purpose of changing into a red black tree is to query efficiently.
1.3 red black tree
Here is an introduction to red and black trees
From: https://www.cnblogs.com/skywang12345/p/3245399.html
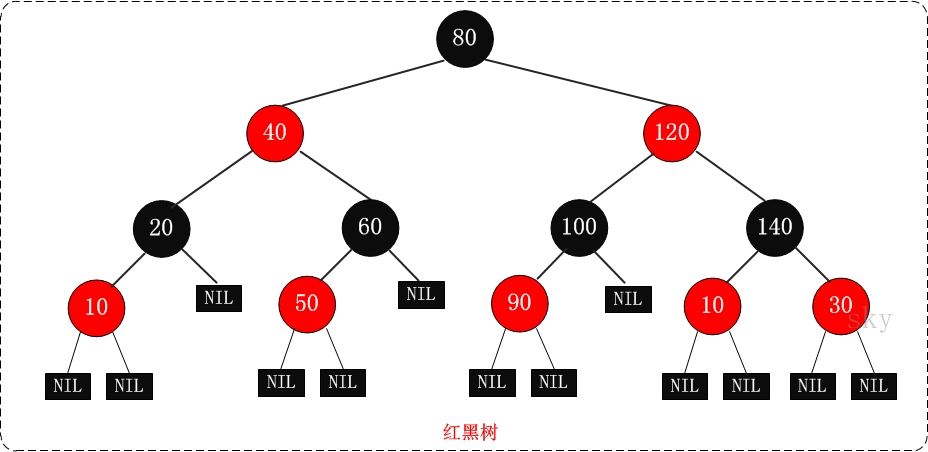
R-B Tree, the full name is red black tree, also known as "red black tree", which is a special binary search tree. Each node of the red black tree has storage bits to represent the color of the node, which can be red or black.
Characteristics of red black tree:
(1) Each node is either black or red.
(2) The root node is black.
(3) Each leaf node (NIL) is black. [Note: the leaf node here refers to the leaf node that is empty (nil or null!]
(4) If a node is red, its child nodes must be black.
(5) All paths from a node to its descendants contain the same number of black nodes.
be careful:
(01) the leaf node in feature (3) is a node that is only empty (NIL or null).
(02) feature (5) to ensure that no path is twice as long as other paths. Therefore, the red black tree is a binary tree that is relatively close to equilibrium.
Chapter 2 underlying data structure of HashMap
2.1 process of storing data
Example code:
HashMap<String, Integer> map = new HashMap<>(); map.put("Liuyan", 18); map.put("Yang Mi", 28); map.put("Lau Andy", 40); map.put("Liuyan", 20);
Output results:
{Yang Mi=28, Liuyan=20, Lau Andy=40}
analysis:
1. When creating a HashMap collection object, the HashMap construction method does not create an array, but creates an array Node[] table (Entry[] table before jdk1.8) with a length of 16 when calling the put method for the first time to store key value pair data.
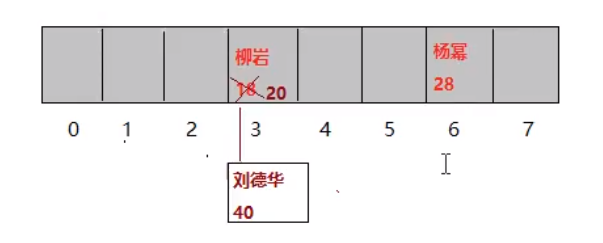
2. Assume that < Liuyan, 18 > data is stored in the hash table, calculate the value according to Liuyan's call to the rewritten hashCode() method in the String class, and then use some algorithm to calculate the index value of the space storing data in the Node array in combination with the array length. If there is no data in the calculated index space, < Liuyan, 18 > is directly stored in the array. (example: the calculated index is 3)
3. Store the data < Andy Lau, 40 > in the hash table. Assuming that the index value calculated by the hashCode() method combined with the ancestor length is also 3, then the array space is not null. At this time, the bottom layer will compare whether the hash values of Liu Yan and Andy Lau are consistent. If not, draw a node in the space to store the key value pair data pair < Andy Lau, 40 >, This method is called zipper method.
4. Assuming that the data < Liuyan, 20 > is stored in the hash table, first calculate that the index must be 3 according to Liuyan's call of hashCode() method combined with the array length. At this time, compare whether the hash values of the stored data Liuyan and the existing data are equal. If the hash values are equal, a hash collision occurs. Then, the bottom layer will call the equals() method in the String of Liu Yan's class to compare whether the two contents are equal:
- Equal: overwrite the previous value with the value of the data added later.
- Unequal: continue to compare the key s of other data. If they are not equal, draw a node to store data. If the node length, that is, the linked list length, is greater than the threshold 8 and the array length is greater than 64, the linked list will become a red black tree.
The process of storing data
5. In the process of constantly adding data, the problem of capacity expansion will be involved. When the threshold is exceeded (and the location to be stored is not empty), the capacity will be expanded. Default capacity expansion method: expand the capacity to twice the original capacity and copy the original data.
6. To sum up, when there are many elements in a table, that is, there are many elements with equal hash values but unequal contents, the efficiency of sequential search through key values is low. In jdk1.8, the hash table is stored by array + linked list + red black tree. When the length (threshold) of the linked list exceeds 8 and the length of the current array is greater than 64, the linked list is converted to red black tree, which greatly reduces the search time.
In short, the hash table is implemented by array + linked list + red black tree (JDK1.8 adds the red black tree part). As shown in the figure below:
7. Further reasons for introducing red black tree into JDK1.8:
Before jdk1.8, the implementation of HashMap was array + linked list. Even if the hash function is better, it is difficult to achieve 100% uniform distribution of elements. When a large number of elements in the HashMap are stored in the same bucket, there is a long linked list under the bucket. At this time, HashMap is equivalent to a single linked list. If the single linked list has n elements, the traversal time complexity is O(n), which completely loses its advantage.
To solve this problem, a red black tree (the search time complexity is O(logn)) is introduced in jdk1.8 to optimize this problem. When the length of the linked list is very small, the traversal speed is very fast, but when the length of the linked list continues to grow, it will certainly have a certain impact on the query performance, so it needs to be transformed into a tree.
There may be multiple elements in the same location in the hash table. In order to deal with the hash conflict, each location in the hash table is represented as a hash bucket.
8. Summary: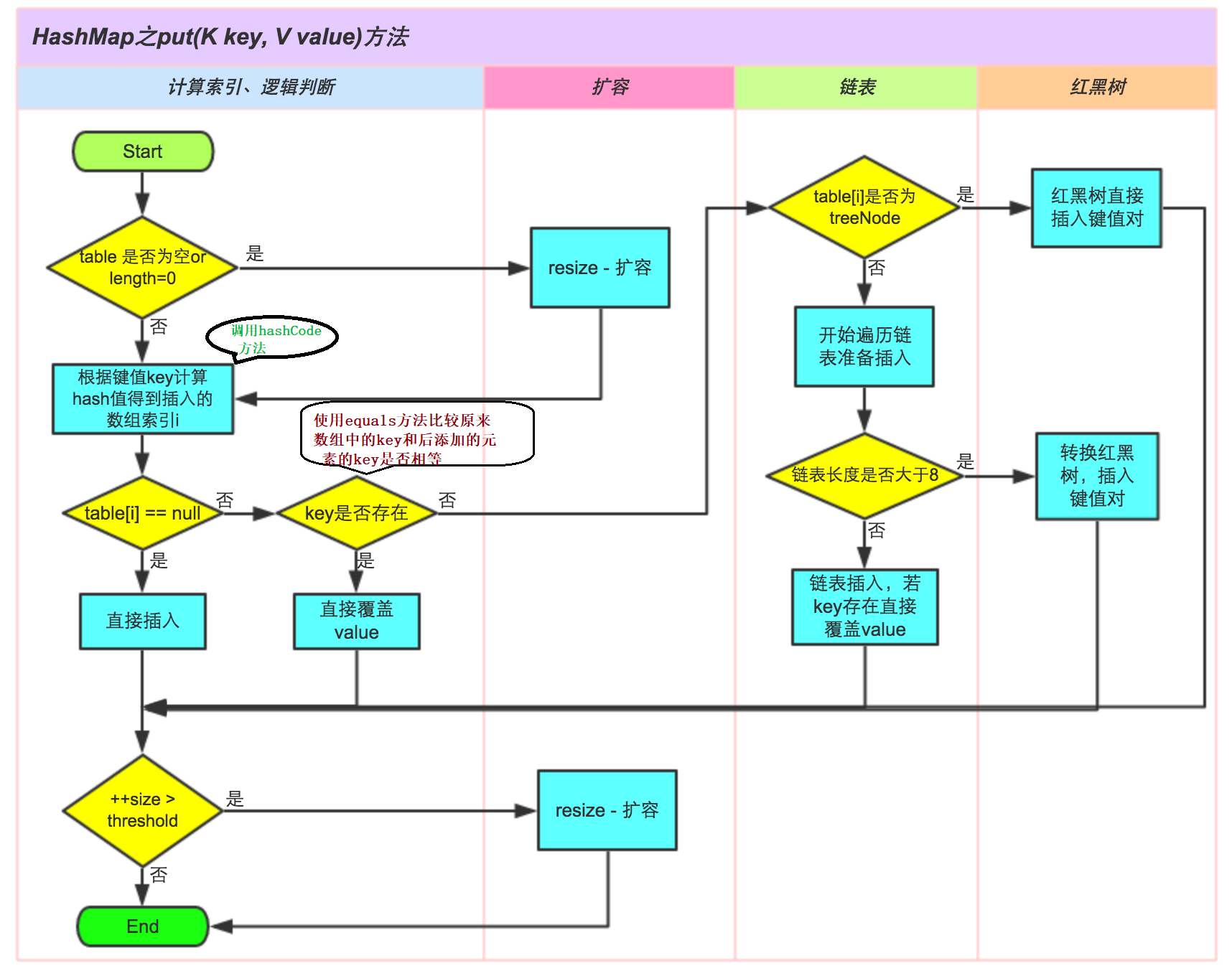
explain:
- size indicates the real-time number of key value pairs in HashMap. Note that this is not equal to the length of the array.
- threshold = capacity * loadFactor. This value is the maximum currently occupied array length. If the size exceeds this value, resize again. The HashMap capacity after expansion is twice the previous capacity.
2.2 interview questions
How is the hash function implemented in HashMap? What are the implementation methods of hash functions?
A: for the hashCode of the key, perform the hash operation, move the unsigned right 16 () bits, and then perform the XOR operation. There are also square middle method, pseudo-random number method and remainder method. These three kinds of efficiency are relatively low. The operation efficiency of unsigned right shift 16 bit XOR is the highest.
What happens when the hashcodes of two objects are equal?
A: hash collision will occur. If the content of the key value is the same, replace the old value. Different key values are connected to the back of the linked list. If the length of the linked list exceeds the threshold 8, it will be converted to red black tree storage.
What is hash collision and how to solve it?
A: as long as the hash code values calculated by the key s of the two elements are the same, hash collision will occur. jdk8 previously used linked lists to resolve hash collisions. jdk8 then uses linked list + red black tree to solve hash collision.
If the hashcodes of two keys are the same, how to store key value pairs?
A: compare whether the contents are the same through equals. Same: the new value overwrites the previous value. Different: the new key value pair is added to the hash table.
Chapter 3 HashMap inheritance relationship
The inheritance relationship of HashMap is shown in the following figure:
explain:
-
Cloneable is an empty interface, indicating that it can be cloned. Create and return a copy of the HashMap object.
-
Serializable serialization interface. It is a marked interface. HashMap objects can be serialized and deserialized.
-
The AbstractMap parent class provides the Map implementation interface. To minimize the effort required to implement this interface.
Add: through the above inheritance relationship, we find a strange phenomenon that HashMap has inherited AbstractMap and AbstractMap class implements the Map interface. Why is HashMap implementing the Map interface? This structure is also found in ArrayList and LinkedList.
According to Josh Bloch, the founder of the java collection framework, this writing is a mistake. In the java collection framework, there are many ways to write like this. When he first wrote the java collection framework, he thought it might be valuable in some places until he realized that he was wrong. Obviously, JDK maintainers didn't think this small mistake was worth modifying, so it existed.
Chapter 4. Members of HashMap collection class
4.1 member variables
4.1.1 serialVersionUID
Serialized version number
private static final long serialVersionUID = 362498820763181265L;
4.1.2 DEFAULT_INITIAL_CAPACITY
Initialization capacity of the collection (must be the nth power of 2)
// The default initial capacity is 16 1 << 4 Equivalent to 1*2 The fourth power of static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
Question: why must it be the n-th power of 2? What happens if the input value is not a power of 2, such as 10?
According to the above explanation, when adding an element to the HashMap, we need to determine its specific position in the array according to the hash value of the key. In order to access efficiently and reduce collisions, HashMap is to distribute the data evenly as much as possible, and the length of each linked list is roughly the same. The key to this implementation is the algorithm of which linked list to store the data.
This algorithm is actually modular, hash% length. The efficiency of direct complement in computer is not as high as that of displacement operation. Therefore, the source code is optimized to use hash & (length - 1). In fact, the premise that hash% length is equal to hash & (length - 1) is that length is the nth power of 2.
Why can this be evenly distributed to reduce collisions? The n-th power of 2 is actually n zeros after 1, and the n-th power-1 of 2 is actually n ones;
give an example:
Description: bitwise and operation: when the same binary digit is 1, the result is 1, otherwise it is zero.
For example, when the length is 8, 3&(8-1)=3 2&(8-1)=2 ,No collision at different positions; For example, length length When it is 8, 8 is the third power of 2. Binary is:1000 length-1 Binary operation: 1000 - 1 --------------------- 111 As follows: hash&(length-1) 3 &(8 - 1)=3 00000011 3 hash & 00000111 7 length-1 --------------------- 00000011----->3 Array subscript hash&(length-1) 2 & (8 - 1) = 2 00000010 2 hash & 00000111 7 length-1 --------------------- 00000010----->2 Array subscript Note: the above calculation results are at different positions without collision; For example, when the length is 9,3&(9-1)=0 2&(9-1)=0 ,All on 0, collided; For example, length length For 9, 9 is not 2 n Power. Binary is:00001001 length-1 Binary operation: 1001 - 1 --------------------- 1000 As follows: hash&(length-1) 3 &(9 - 1)=0 00000011 3 hash & 00001000 8 length-1 --------------------- 00000000----->0 Array subscript hash&(length-1) 2 & (9 - 1) = 2 00000010 2 hash & 00001000 8 length-1 --------------------- 00000000----->0 Array subscript Note: the above calculation results are all above 0, and the collision occurs
Note: of course, if the efficiency is not considered, the remainder can be obtained directly (there is no need to require that the length must be the nth power of 2)
Summary:
1. As can be seen from the above, when we determine the position of the key in the array according to the hash, if n is the power of 2, we can ensure the uniform insertion of data. If n is not the power of 2, we may never insert data in some positions of the array, wasting the space of the array and increasing the hash conflict.
2. On the other hand, we may want to determine the position by% remainder, which is OK, but the performance is not as good as & operation. And when n is the power of 2: hash & (length - 1) = = hash% length
3. Therefore, the reason why the hashmap capacity is power-2 is to evenly distribute the data and reduce hash conflicts. After all, the greater the hash conflict, the greater the length of a chain in the representative array, which will reduce the performance of hashmap
4. When creating a HashMap object, if the length of the input array is 10, not the power of 2, the HashMap must obtain the power of 2 through one-pass displacement operation and or operation, and it is the nearest number to that number.
The source code is as follows:
//establish HashMap The specified array length is 10, not a power of 2 HashMap hashMap = new HashMap(10); public HashMap(int initialCapacity) {//initialCapacity=10 this(initialCapacity, DEFAULT_LOAD_FACTOR); } public HashMap(int initialCapacity, float loadFactor) {//initialCapacity=10 if (initialCapacity < 0) throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity); if (initialCapacity > MAXIMUM_CAPACITY) initialCapacity = MAXIMUM_CAPACITY; if (loadFactor <= 0 || Float.isNaN(loadFactor)) throw new IllegalArgumentException("Illegal load factor: " + loadFactor); this.loadFactor = loadFactor; this.threshold = tableSizeFor(initialCapacity);//initialCapacity=10 } /** * Returns a power of two size for the given target capacity. */ static final int tableSizeFor(int cap) {//int cap = 10 int n = cap - 1; n |= n >>> 1; n |= n >>> 2; n |= n >>> 4; n |= n >>> 8; n |= n >>> 16; return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; }
explain:
It can be seen that when instantiating a HashMap instance, if initialCapacity (assumed to be 10) is given, since the capacity of the HashMap must be a power of 2, this method is used to find the power of the smallest 2 greater than or equal to initialCapacity (assumed to be 10) (if initialCapacity is a power of 2, this number is returned).
analysis:
int n = cap - 1;
Prevent cap is already a power of 2. If the cap is already a power of 2 and there is no such minus 1 operation, the returned capacity will be twice that of the cap after performing the following unsigned operations.
If n is 0 at this time (after cap - 1), it is still 0 after several unsigned right shifts, and the last returned capacity is 1 (there is an n + 1 operation at last).
First shift right:
int n = cap - 1;//cap=10 n=9 n |= n >>> 1; 00000000 00000000 00000000 00001001 //9 | 00000000 00000000 00000000 00000100 //9 Change to 4 after moving right ------------------------------------------------- 00000000 00000000 00000000 00001101 //Bitwise XOR is followed by 13
Since n is not equal to 0, there will always be a bit of 1 in the binary representation of N. at this time, the highest bit 1 is considered. By moving 1 bit to the right without sign, the highest bit 1 is moved to the right by 1 bit, and then do or operation, so that the right bit immediately adjacent to the highest bit 1 in the binary representation of n is also 1, such as:
00000000 00000000 00000000 00001101
Second shift right:
n |= n >>> 2;//n Through the first shift to the right, it becomes: n=13 00000000 00000000 00000000 00001101 // 13 | 00000000 00000000 00000000 00000011 //13 Change to 3 after moving right ------------------------------------------------- 00000000 00000000 00000000 00001111 //Bitwise XOR is followed by 15
Note that this n has passed n | = n > > > 1; Operation. Assuming that n is 00000000 00000000 00000000 00001101 at this time, n moves two unsigned right bits, which will move the two consecutive ones in the highest bit to the right two bits, and then do or operate with the original n, so that there will be four consecutive ones in the high bit of the binary representation of n. For example:
00000000 00000000 00000000 00001111 //Bitwise XOR is followed by 15
Third shift right:
n |= n >>> 4;//n Through the first and second right shifts, it becomes: n=15 00000000 00000000 00000000 00001111 // 15 | 00000000 00000000 00000000 00000000 //15 Change to 0 after moving right ------------------------------------------------- 00000000 00000000 00000000 00001111 //Bitwise XOR is followed by 15
This time, move the four consecutive ones in the existing high order to the right by 4 bits, and then do or operation. In this way, there will normally be 8 consecutive ones in the high order of the binary representation of n. Such as 00001111 1111xxxxxx. and so on
Note: the maximum capacity is a positive number of 32bit, so the last n | = n > > > 16; At most, there are 32 1s (but this is already a negative number. Before executing tableSizeFor, judge the initialCapacity if it is greater than the MAXIMUM_CAPACITY(2 ^ 30) , the maximum _capabilityis taken. If it is equal to the maximum _capability, the displacement operation will be performed. Therefore, after the displacement operation, the maximum 30 1s will not be greater than or equal to the maximum _capability. 30 1s plus 1 will get 2 ^ 30).
Complete example: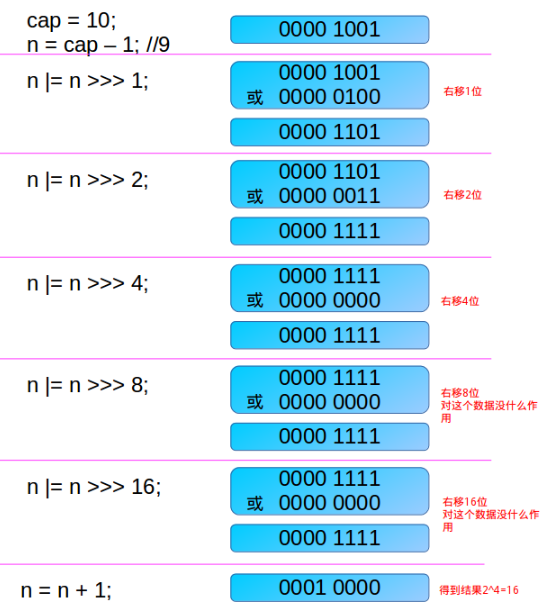
Note: the obtained capacity is assigned to threshold.
this.threshold = tableSizeFor(initialCapacity);
4.1.3 DEFAULT_LOAD_FACTOR
Default load factor (default 0.75)
static final float DEFAULT_LOAD_FACTOR = 0.75f;
4.1.4 MAXIMUM_CAPACITY
Set maximum capacity
static final int MAXIMUM_CAPACITY = 1 << 30; // 2 The 30th power of
4.1.5 TREEIFY_THRESHOLD
When the value of the linked list exceeds 8, it will turn into a red black tree (new in jdk1.8)
// When bucket( bucket)When the number of nodes on is greater than this value, it will be converted to a red black tree static final int TREEIFY_THRESHOLD = 8;
Question: why is the number of nodes in the Map bucket more than 8 before turning into a red black tree?
8 this threshold is defined in HashMap. For this member variable, the comments on the source code only indicate that 8 is the threshold for bin (bin is a bucket) to be converted from a linked list to a tree, but do not explain why it is 8:
There is a comment in HashMap that says: let's continue to look at:
Because TreeNodes are about twice the size of regular nodes, we use them only when bins contain enough nodes to warrant use (see TREEIFY_THRESHOLD). And when they become too small (due to removal or resizing) they are converted back to plain bins. In usages with well-distributed user hashCodes, tree bins are rarely used. Ideally, under random hashCodes, the frequency of nodes in bins follows a Poisson distribution (http://en.wikipedia.org/wiki/Poisson_distribution) with a parameter of about 0.5 on average for the default resizing threshold of 0.75, although with a large variance because of resizing granularity. Ignoring variance, the expected occurrences of list size k are (exp(-0.5)*pow(0.5, k)/factorial(k)). The first values are: Because the size of tree nodes is about twice that of ordinary nodes, we use tree nodes only when the box contains enough nodes(See TREEIFY_THRESHOLD). When they get too small(Due to deletion or resizing)It will be converted back to the ordinary bucket when using well distributed users hashcode Ideally, in the case of random hash code, the frequency of nodes in the box follows Poisson distribution (http://en.wikipedia.org/wiki/Poisson_distribution),The default adjustment threshold is 0.75,The average parameter is about 0.5,Although there are great differences due to the adjustment granularity. Ignore the variance and reduce the list size k The expected number of occurrences is(exp(-0.5)*pow(0.5, k)/factorial(k)). The first value is: 0: 0.60653066 1: 0.30326533 2: 0.07581633 3: 0.01263606 4: 0.00157952 5: 0.00015795 6: 0.00001316 7: 0.00000094 8: 0.00000006 more: less than 1 in ten million
TreeNodes takes up twice as much space as ordinary Nodes, so only when the bin contains enough Nodes will it be converted to TreeNodes, and whether there are enough Nodes is determined by the value of tree_threshold. When the number of Nodes in the bin decreases, it will be converted to ordinary bin. And when we check the source code, we find that when the length of the linked list reaches 8, it will be converted to red black tree, and when the length decreases to 6, it will be converted to ordinary B in.
This explains why it is not converted to TreeNodes at the beginning, but requires a certain number of nodes to be converted to TreeNodes. In short, it is a trade-off between space and time.
This paragraph also says: when the hashCode has good discreteness, the probability of using tree bin is very small, because the data is evenly distributed in each bin, and the length of the linked list in almost no bin will reach the threshold. However, under random hashCode, the discreteness may become worse. However, JDK can not prevent users from implementing this bad hash algorithm, so it may lead to uneven numbers According to the distribution. However, ideally, the distribution frequency of all nodes in the bin under the random hashCode algorithm will follow the Poisson distribution. We can see that the probability that the length of the linked list in a bin reaches 8 elements is 0.00000006, which is almost impossible. Therefore, the reason why 8 is selected is not determined casually, but determined according to probability statistics. It can be seen that it has developed for nearly 30 years Every change and optimization of Java is very rigorous and scientific.
That is to say, 8 conforms to the Poisson distribution. When it exceeds 8, the probability is very small, so we choose 8.
Supplement:
1) Poisson distribution (Poisson distribution) is a discrete [probability distribution] commonly seen in statistics and probability.
The probability function of Poisson distribution is:
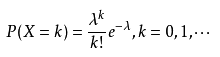
Parameters of Poisson distribution λ Is the average number of random events per unit time (or unit area). Poisson distribution is suitable to describe the number of random events in unit time.
When there are many inserted nodes, the probability of hash collision is very small according to Poisson distribution. At this time, the red black tree is used to replace the linked list. The insertion is basically direct insertion without left-hand and right-hand operations
2) The following is the explanation I read on some materials when studying this problem: for your reference:
The average search length of the red black tree is log(n). If the length is 8, the average search length is log(8)=3, and the average search length of the linked list is n/2. When the length is 8, the average search length is 8 / 2 = 4, which is necessary to convert into a tree; If the length of the linked list is less than or equal to 6, 6 / 2 = 3, and log(6)=2.6, although the speed is also very fast, the time to convert into tree structure and generate tree will not be too short.
4.1.6 UNTREEIFY_THRESHOLD
When the value of the linked list is less than 6, it will be transferred back from the red black tree to the linked list
// When bucket( bucket)If the number of nodes on is less than this value, the tree will be converted to a linked list static final int UNTREEIFY_THRESHOLD = 6;
4.1.7 MIN_TREEIFY_CAPACITY
When the number in the Map exceeds this value, the bucket in the table can be tree shaped. Otherwise, when there are too many elements in the bucket, it will be expanded instead of tree shaped. In order to avoid the conflict between expansion and tree shaped selection, this value cannot be less than 4 * tree_threshold (8)
// The structure in the bucket is converted to the value with the smallest array length corresponding to the red black tree static final int MIN_TREEIFY_CAPACITY = 64;
4.1.8 table
table is used to initialize (must be the n-th power of two) (key)
// An array of storage elements transient Node<K,V>[] table;
In jdk1.8, we know that HashMap is a structure composed of array, linked list and red black tree. table is the array in HashMap. Before jdk8, the array type was entry < K, V >. From jdk1.8, there are node < K, V > types. Just changed the name and implemented the same interface: map. Entry < K, V >. Responsible for storing the key value to the data.
4.1.9 entrySet
Used to store cache
// A collection of concrete elements transient Set<Map.Entry<K,V>> entrySet;
4.1.10 size
Number of elements stored in HashMap (key)
// Store the number of elements. Note that this is not equal to the length of the array transient int size;
size is the real-time quantity of K-V in HashMap, not the length of array table.
4.1.11 modCount
Used to record the modification times of HashMap
// Each expansion and change map Structure counter transient int modCount;
4.1.12 threshold
The value used to resize the next capacity is calculated as (capacity * load factor)
// Critical value actual size (capacity)*When the load factor) exceeds the critical value, the capacity will be expanded int threshold;
4.1.13 loadFactor
Load factor of hash table (emphasis)
// Load factor final float loadFactor;
explain:
- loadFactor is used to measure the full degree of HashMap, which indicates the density of HashMap and affects the probability of hash operation to the same array location. The method to calculate the real-time load factor of HashMap is size/capacity, rather than the number of buckets occupied, and the capacity is removed. Capacity is the number of buckets, that is, the length of the table.
- Too large loadFactor leads to low efficiency in finding elements, too small leads to low utilization of arrays, and the stored data will be very scattered. The default value of loadFactor is 0.75f, which is a good critical value officially given.
- When the elements contained in the HashMap have reached 75% of the length of the HashMap array, it means that the HashMap is too crowded and needs to be expanded. The process of capacity expansion involves rehash, copying data and other operations, which is very performance consuming. Therefore, the number of capacity expansion can be minimized in development, which can be avoided by specifying the initial capacity when creating HashMap collection objects.
- loadFactor can be customized in the constructor of HashMap.
// Construction method to construct an empty space with a specified initial capacity and load factor HashMap HashMap(int initialCapacity, float loadFactor);
Why is the load factor set to 0.75 and the initialization threshold 12?
The closer the loadFactor is to 1, the more data (entries) stored in the array will be, and the more dense it will be, that is, the length of the linked list will increase. The smaller the loadFactor is, that is, it will approach 0, and the less data (entries) stored in the array will be, and the more sparse it will be.
If you want the linked list to be as few as possible, you should expand it in advance. Some array spaces may not store data all the time, and the load factor should be as small as possible.
give an example:
For example, the load factor is 0.4. So 16*0.4--->6 If the array is expanded when it is full of 6 spaces, the utilization of the array will be too low.
The load factor is 0.9. So 16*0.9--->14 Then this will lead to a little more linked lists and low efficiency of finding elements.
Therefore, both the array utilization and the linked list should not be too much. After a lot of tests, 0.75 is the best scheme.
- threshold calculation formula: capacity (array length is 16 by default) * LoadFactor (load factor is 0.75 by default).
This value is the maximum currently occupied array length. When size > = threshold, you should consider resizing the array, that is, this means a standard to measure whether the array needs to be expanded. The HashMap capacity after expansion is twice as large as that before.
4.2 construction method
Important construction methods in HashMap are as follows:
4.2.1 HashMap()
Construct an empty HashMap with default initial capacity (16) and default load factor (0.75).
public HashMap() { this.loadFactor = DEFAULT_LOAD_FACTOR; // Set the default load factor to 0.75 Assign to loadFactor,Array was not created }
4.2.2 HashMap(int initialCapacity)
Construct a HashMap with the specified initial capacity and default load factor (0.75).
// Specifies the constructor for capacity size public HashMap(int initialCapacity) { this(initialCapacity, DEFAULT_LOAD_FACTOR); }
4.2.3 HashMap(int initialCapacity, float loadFactor)
Construct a HashMap with a specified initial capacity and load factor.
/* Specifies the constructor for capacity size and load factor initialCapacity: Specified capacity loadFactor:Specified load factor */ public HashMap(int initialCapacity, float loadFactor) { // Determine initialization capacity initialCapacity Is it less than 0 if (initialCapacity < 0) // If it is less than 0, an illegal parameter exception is thrown IllegalArgumentException throw new IllegalArgumentException("Illegal initial capacity: " + initialCapacity); // Determine initialization capacity initialCapacity Is it greater than the maximum capacity of the collection MAXIMUM_CAPACITY if (initialCapacity > MAXIMUM_CAPACITY) // If more than MAXIMUM_CAPACITY,Will MAXIMUM_CAPACITY Assign to initialCapacity initialCapacity = MAXIMUM_CAPACITY; // Judge load factor loadFactor Is it less than or equal to 0 or is it a non numeric value if (loadFactor <= 0 || Float.isNaN(loadFactor)) // If one of the above conditions is met, an illegal parameter exception is thrown IllegalArgumentException throw new IllegalArgumentException("Illegal load factor: " + loadFactor); // Assign the specified load factor to HashMap Load factor of member variable loadFactor this.loadFactor = loadFactor; this.threshold = tableSizeFor(initialCapacity); } // Finally called. tableSizeFor,Let's look at the method implementation: /* Returns the n-th power of the smallest 2 larger than the specified initialization capacity */ static final int tableSizeFor(int cap) { int n = cap - 1; n |= n >>> 1; n |= n >>> 2; n |= n >>> 4; n |= n >>> 8; n |= n >>> 16; return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1; }
explain:
For javathis.threshold = tableSizeFor(initialCapacity); Answers to questions:
tableSizeFor(initialCapacity) determines whether the specified initialization capacity is the nth power of 2. If not, it will become the smallest nth power of 2 greater than the specified initialization capacity. However, note that the calculated data is returned to the call in the tableSizeFor method body, and is directly assigned to the threshold boundary value. Some people will think that this is a bug, which should be written as follows: this.threshold = tableSizeFor(initialCapacity) * this.loadFactor; Only in this way can it meet the meaning of threshold (the capacity will be expanded when the size of HashMap reaches the threshold). However, please note that in the construction methods after jdk8, the member variable table is not initialized. The initialization of table is postponed to the put method, where the threshold will be recalculated.
4.2.4 HashMap(Map<? extends K, ? extends V> m)
Constructor containing another "Map"
// Construct a mapping relationship and specify Map Same new HashMap. public HashMap(Map<? extends K, ? extends V> m) { // Load factor loadFactor Becomes the default load factor of 0.75 this.loadFactor = DEFAULT_LOAD_FACTOR; putMapEntries(m, false); }
Finally, we call putMapEntries() to see how the method is implemented:
final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict) { //Gets the length of the parameter set int s = m.size(); if (s > 0) { //Judge whether the length of the parameter set is greater than 0, indicating that it is greater than 0 if (table == null) { // judge table Has it been initialized // Uninitialized, s by m Actual number of elements float ft = ((float)s / loadFactor) + 1.0F; int t = ((ft < (float)MAXIMUM_CAPACITY) ? (int)ft : MAXIMUM_CAPACITY); // Calculated t Greater than the threshold, initialize the threshold if (t > threshold) threshold = tableSizeFor(t); } // Initialized, and m If the number of elements is greater than the threshold, expand the capacity else if (s > threshold) resize(); // take m Add all elements in to HashMap in for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) { K key = e.getKey(); V value = e.getValue(); putVal(hash(key), key, value, false, evict); } } }
be careful:
float ft = ((float)s / loadFactor) + 1.0F; Why add 1.0F to this line of code?
The result of s/loadFactor is decimal. Adding 1.0F is equivalent to (int)ft. therefore, the decimal is rounded up to ensure greater capacity as much as possible. Greater capacity can reduce the number of calls to resize. So + 1.0F is to get more capacity.
For example, if the number of elements in the original set is 6, then 6 / 0.75 is 8, which is the n-power of 2, then the size of the new array is 8. Then, the data of the original array will be stored in a new array with a length of 8. This will lead to insufficient capacity and continuous capacity expansion when storing elements, so the performance will be reduced. If + 1, the array length will directly change to 16, which can reduce the capacity expansion of the array.
4.3 membership method
4.3.1 adding method
The put method is complex, and the implementation steps are as follows:
1) First, calculate the bucket to which the key is mapped through the hash value;
2) If there is no collision on the barrel, insert it directly;
3) If a collision occurs, you need to deal with the conflict:
- If the bucket uses a red black tree to handle conflicts, the method of the red black tree is called to insert data;
- Otherwise, the traditional chain method is used to insert. If the length of the chain reaches the critical value, the chain is transformed into a red black tree;
4) If there is a duplicate key in the bucket, replace the key with the new value value;
5) If the size is greater than the threshold, expand the capacity;
The specific methods are as follows:
public V put(K key, V value) { return putVal(hash(key), key, value, false, true); }
explain:
1) HashMap only provides put for adding elements, and putVal method is only a method called for put method, which is not provided to users. So we focus on the putVal method.
2) We can see that in the putVal() method, the key executes the hash() method here to see how the Hash method is implemented.
static final int hash(Object key) { int h; /* 1)If key equals null: You can see that when the key is equal to null, there is also a hash value, and the returned value is 0 2)If key is not equal to null: Firstly, the hashCode of the key is calculated and assigned to h, and then the hash value is obtained by bitwise XOR with the binary after H unsigned right shift of 16 bits */ return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); }
It can be seen from the above that HashMap supports empty key, while HashTable directly uses the key to obtain HashCode, so an exception will be thrown if the key is empty.
In fact, the above has explained why the length of HashMap should be a power of 2, because the method used by HashMap is very clever. It obtains the save bit of the object through hash & (table. Length - 1). As mentioned earlier, the length of the underlying array of HashMap is always the nth power of 2, which is the speed optimization of HashMap. When length is always to the nth power of 2, hash & (length-1) operation is equivalent to modulo length, that is, hash%length, but & is more efficient than%. For ex amp le, n% 32 = n & (32 - 1).
Interpret the above hash method:
Let's first study how the hash value of the key is calculated. The hash value of key is calculated by the above method.
This hash method first calculates the hashCode of the key and assigns it to h, and then performs bitwise XOR with the binary after H unsigned right shift of 16 bits to obtain the final hash value. The calculation process is as follows:
static final int hash(Object key) { int h; /* 1)If key equals null: You can see that when the key is equal to null, there is also a hash value, and the returned value is 0 2)If key is not equal to null: Firstly, the hashCode of the key is calculated and assigned to h, and then the hash value is obtained by bitwise XOR with the binary after H unsigned right shift of 16 bits */ return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); }
The hash value calculated by the above hash function is used in the putVal function:
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { . . . . . . . . . . . . . . if ((p = tab[i = (n - 1) & hash]) == null)//there n Represents the array length 16 . . . . . . . . . . . . . . }
The calculation process is as follows:
explain:
1)key.hashCode(); Returns the hash value, that is, hashcode. Suppose you randomly generate a value.
2) n indicates that the length of array initialization is 16
3) & (bitwise and operation): operation rule: when the same binary digit is 1, the result is 1, otherwise it is zero.
4) ^ (bitwise XOR operation): operation rules: on the same binary digit, the number is the same, the result is 0, and the difference is 1.

In short:
-
The high 16 bits remain unchanged, and the low 16 bits and high 16 bits make an XOR (the obtained hashcode is converted into 32-bit binary, and the low 16 bits and high 16 bits of the first 16 bits and the last 16 bits make an XOR)
Question: why do you do this?
If n, that is, the array length is very small, assuming 16, then n-1 is -- "1111. Such a value and hashCode() directly perform bitwise and operations. In fact, only the last four bits of the hash value are used. If the high-order change of the hash value is large and the low-order change is small, it is easy to cause hash conflict. Therefore, the high-order and low-order are used here to solve this problem.
For example:
hashCode() value: 1111 1111 1111 1111 1111 0000 1110 1010
&
n-1 is 16-1 -- "15: . . . . . . . . . . . . . . . . . . . . . . one thousand one hundred and eleven
-------------------------------------------------------------------
0000 0000 0000 0000 1010 ---- "10 as index
In fact, the hashCode value is used as the array index. If the next high hashCode is inconsistent and the low hashCode is consistent, the calculated index will still be 10, resulting in hash conflict. Reduce performance. -
(n-1) & hash = - > the subscript (n-1) n indicates the array length of 16, and N-1 is 15
-
The essence of remainder is to divide constantly and subtract the remaining numbers. The operation efficiency is lower than that of bit operation.
Now look at the putVal() method and see what it does.
Main parameters:
-
Hash value of hash key
-
Key original key
-
Value the value to store
-
onlyIfAbsent if true means that the existing value will not be changed
-
If evict is false, it means that the table is in creation status
The source code of putVal() method is as follows:
public V put(K key, V value) { return putVal(hash(key), key, value, false, true); } final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) { Node<K,V>[] tab; Node<K,V> p; int n, i; /* 1)transient Node<K,V>[] table; Represents an array that stores elements in a Map collection. 2)(tab = table) == null It means to assign an empty table to tab, and then judge whether tab is equal to null. It must be null for the first time 3)(n = tab.length) == 0 Indicates that the length of the array 0 is assigned to N, and then judge whether n is equal to 0 and N is equal to 0 Since the if judges to use double or, if only one is satisfied, execute the code n = (tab = resize()).length; Perform array initialization. And assign the initialized array length to n 4)After executing n = (tab = resize()).length, each space of array tab is null */ if ((tab = table) == null || (n = tab.length) == 0) n = (tab = resize()).length; /* 1)i = (n - 1) & hash Indicates that the index of the calculated array is assigned to i, that is, to determine which bucket the elements are stored in 2)p = tab[i = (n - 1) & hash]Indicates that the data of the calculated position is obtained and assigned to node p 3) (p = tab[i = (n - 1) & hash]) == null Judge whether the node position is equal to null. If it is null, execute the code: tab[i] = newNode(hash, key, value, null); Create a new node according to the key value pair and put it into the bucket at that position Summary: if there is no hash collision conflict in the current bucket, the key value pair is directly inserted into the spatial location */ if ((p = tab[i = (n - 1) & hash]) == null) //Create a new node and store it in the bucket tab[i] = newNode(hash, key, value, null); else { // implement else explain tab[i]Not equal to null,Indicates that this position already has a value. Node<K,V> e; K k; /* Compare whether the hash value and key of the first element in the bucket (node in the array) are equal 1)p.hash == hash : p.hash Indicates the hash value of the existing data. Hash indicates the hash value of the added data. Compare whether the two hash values are equal Note: p represents tab[i], that is, the Node object returned by the newNode(hash, key, value, null) method. Node<K,V> newNode(int hash, K key, V value, Node<K,V> next) { return new Node<>(hash, key, value, next); } In the Node class, there is a member variable hash, which is used to record the hash value of the previous data 2)(k = p.key) == key : p.key Get the key of the original data, assign it to K key, and then add the key of the data. Compare whether the address values of the two keys are equal 3)key != null && key.equals(k): If the address values of the two keys are not equal, first judge whether the added key is equal to null. If not, call the equals method to judge whether the contents of the two keys are equal */ if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) /* Note: the hash values of the two elements are equal, and the value of the key is also equal Assign the old element whole object to e and record it with E */ e = p; // hash Values are not equal or key Unequal; judge p Is it a red black tree node else if (p instanceof TreeNode) // Put it in the tree e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value); // Description is a linked list node else { /* 1)If it is a linked list, you need to traverse to the last node and insert it 2)Loop traversal is used to judge whether there are duplicate key s in the linked list */ for (int binCount = 0; ; ++binCount) { /* 1)e = p.next Get the next element of p and assign it to e 2)(e = p.next) == null Judge whether p.next is equal to null. If it is equal to null, it means that P has no next element. At this time, it reaches the tail of the linked list and no duplicate key has been found, it means that the HashMap does not contain the key Insert the key value pair into the linked list */ if ((e = p.next) == null) { /* 1)Create a new node and insert it into the tail p.next = newNode(hash, key, value, null); Node<K,V> newNode(int hash, K key, V value, Node<K,V> next) { return new Node<>(hash, key, value, next); } Note that the fourth parameter next is null, because the current element is inserted at the end of the linked list, then the next node must be null 2)This addition method also meets the characteristics of linked list data structure, adding new elements backward each time */ p.next = newNode(hash, key, value, null); /* 1)After adding nodes, judge whether the number of nodes is greater than tree_ Threshold 8, if greater than Then the linked list is converted into a red black tree 2)int binCount = 0 : Represents the initialization value of the for loop. Count from 0. Record the number of traversal nodes. A value of 0 indicates the first node and 1 indicates the second node.... 7 represents the eighth node, plus an element in the array. The number of elements is 9 TREEIFY_THRESHOLD - 1 -->8 - 1 --->7 If the value of binCount is 7 (plus an element in the array, the number of elements is 9) TREEIFY_THRESHOLD - 1 It is also 7. At this time, the red black tree is converted */ if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st //Convert to red black tree treeifyBin(tab, hash); // Jump out of loop break; } /* Execution here shows that e = p.next is not null and is not the last element. Continue to judge whether the key value of the node in the linked list is equal to the key value of the inserted element */ if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) // Equal, jump out of loop /* If the key of the element to be added is equal to that of the existing element in the linked list, the for loop will jump out. No more comparisons Directly execute the following if statement to replace if (E! = null) */ break; /* Indicates that the newly added element is not equal to the current node. Continue to find the next node. Used to traverse the linked list in the bucket. Combined with the previous e = p.next, you can traverse the linked list */ p = e; } } /* Indicates that a node whose key value and hash value are equal to the inserted element is found in the bucket In other words, duplicate keys are found through the above operation, so here is to change the value of the key into a new value and return the old value This completes the modification function of the put method */ if (e != null) { // record e of value V oldValue = e.value; // onlyIfAbsent by false Or the old value is null if (!onlyIfAbsent || oldValue == null) //Replace old value with new value //e.value Represents the old value value Represents a new value e.value = value; // Post access callback afterNodeAccess(e); // Return old value return oldValue; } } //Number of records modified ++modCount; // Determine whether the actual size is greater than threshold Threshold, if exceeded, the capacity will be expanded if (++size > threshold) resize(); // Post insert callback afterNodeInsertion(evict); return null; }
4.3.2 treeifyBin method for converting linked list into red black tree
After adding nodes, judge whether the number of nodes is greater than tree_ The threshold value of threshold is 8. If it is greater than 8, the linked list will be converted into a red black tree. The method of converting the red black tree treeifyBin is as follows:
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st //Convert to red black tree tab Represents the array name hash Represents the hash value treeifyBin(tab, hash);
The treeifyBin method is as follows:
/** * Replaces all linked nodes in bin at index for given hash unless * table is too small, in which case resizes instead. Replaces all linked nodes in the bucket at the index of the specified hash table. Unless the table is too small, the size will be modified. Node<K,V>[] tab = tab Array name int hash = hash Represents the hash value */ final void treeifyBin(Node<K,V>[] tab, int hash) { int n, index; Node<K,V> e; /* If the current array is empty or the length of the array is less than the threshold for tree formation (min_tree_capability = 64), Just expand the capacity. Instead of turning the node into a red black tree. Objective: if the array is very small, it is less efficient to convert the red black tree and traverse it. In this case, the capacity is expanded, and the hash value is recalculated ,The length of the linked list may become shorter, and the data will be put into the array, which is relatively more efficient. */ if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) //Capacity expansion method resize(); else if ((e = tab[index = (n - 1) & hash]) != null) { /* 1)The execution here shows that the length of the array in the hash table is greater than the threshold 64, and the tree is started 2)e = tab[index = (n - 1) & hash]Indicates that the elements in the array are taken out and assigned to E. e is the linked list node located in the bucket in the hash table, starting from the first */ //hd: Head node of red black tree tl :Tail node of red black tree TreeNode<K,V> hd = null, tl = null; do { //Create a new tree node, content and current linked list node e agreement TreeNode<K,V> p = replacementTreeNode(e, null); if (tl == null) //New key p The node is assigned to the head node of the red black tree hd = p; else { /* p.prev = tl: Assign the previous node p to the previous node of the current P tl.next = p;Take the current node p as the next node of the tail node of the tree */ p.prev = tl; tl.next = p; } tl = p; /* e = e.next Assign the next node of the current node to e, if the next node is not equal to null Then go back to the above and continue to take out the nodes in the linked list and convert them into red black trees */ } while ((e = e.next) != null); /* Let the first element in the bucket, that is, the element in the array, point to the node of the new red black tree. Later, the element in the bucket is the red black tree Instead of a linked list data structure */ if ((tab[index] = hd) != null) hd.treeify(tab); } }
Summary: the above operations have done the following:
1. Determine whether to expand or tree according to the number of elements in the hash table
2. If it is a tree, traverse the elements in the bucket, create the same number of tree nodes, copy the content and establish a connection
3. Then let the first element in the bucket point to the newly created tree root node, and replace the linked list content of the bucket with tree content
4.3.3 capacity expansion method_ resize
4.3.3.1 capacity expansion mechanism
To understand the capacity expansion mechanism of HashMap, you need to have these two questions
-
1. When is capacity expansion required
-
2. What is the capacity expansion of HashMap
1. When is capacity expansion required
When the number of elements in the HashMap exceeds the array size (array length) * loadFactor, the array will be expanded. The default value of loadFactor (DEFAULT_LOAD_FACTOR) is 0.75, which is a compromise value. That is, by default, the array size is 16, so when the number of elements in the HashMap exceeds 16 × When 0.75 = 12 (this value is the threshold or boundary value threshold value), the size of the array is expanded to 2 × 16 = 32, that is, double the size, and then recalculate the position of each element in the array, which is a very performance consuming operation. Therefore, if we have predicted the number of elements in the HashMap, predicting the number of elements can effectively improve the performance of the HashMap.
Supplement:
When the number of objects in one of the linked lists in the HashMap reaches 8, if the array length does not reach 64, the HashMap will be expanded first. If it reaches 64, the linked list will become a red black tree and the Node type will change from Node to TreeNode. Of course, if the number of nodes in the tree is lower than 6 when the resize method is executed next time after the mapping relationship is removed, the tree will also be converted into a linked list.
2. What is the capacity expansion of HashMap
Capacity expansion will be accompanied by a re hash allocation, and all elements in the hash table will be traversed, which is very time-consuming. When writing programs, try to avoid resize.
The rehash method used by HashMap during capacity expansion is very ingenious, because each capacity expansion is doubled. Compared with the original calculated (n-1) & hash result, there is only one bit more, so the node is either in the original position or assigned to the position of "original position + old capacity".
How to understand? For example, when we expand from 16 to 32, the specific changes are as follows:

Therefore, after the element recalculates the hash, because n becomes twice, the marking range of n-1 is 1 bit more in the high order (red), so the new index will change like this:

Note: 5 is the original index calculated assuming. This verifies the above description: after capacity expansion, the node is either in the original location or assigned to the location of "original location + old capacity".
Therefore, when we expand the HashMap, we do not need to recalculate the hash. We just need to see whether the new bit of the original hash value is 1 or 0. If it is 0, the index remains unchanged. If it is 1, the index becomes "original index + oldcap (original location + old capacity)". The following figure shows the resizing diagram from 16 to 32:
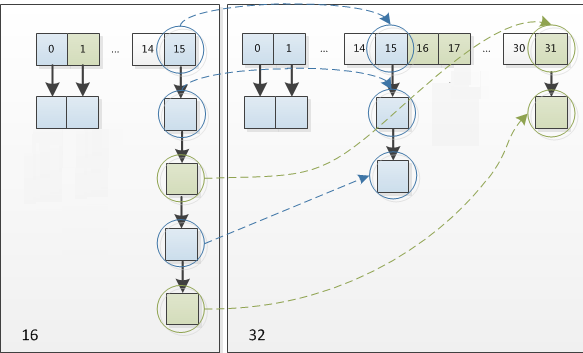
It is precisely because of this ingenious rehash method that not only saves the time to recalculate the hash value, but also because the newly added 1 bit is 0 or 1, it can be considered as random. In the process of resizing, it is ensured that the number of nodes in each bucket after rehash must be less than or equal to the number of nodes in the original bucket, so as to ensure that there will be no more serious hash conflict after rehash, The previously conflicting nodes are evenly dispersed into new buckets.
4.3.3.2 interpretation of source code resize method
The following is the specific implementation of the code:
final Node<K,V>[] resize() { //Get the current array Node<K,V>[] oldTab = table; //If the current array is equal to null Length returns 0, otherwise it returns the length of the current array int oldCap = (oldTab == null) ? 0 : oldTab.length; //The current threshold is 12 by default(16*0.75) int oldThr = threshold; int newCap, newThr = 0; //If the length of the old array is greater than 0 //Start calculating the size after capacity expansion if (oldCap > 0) { // If you exceed the maximum value, you won't expand any more, so you have to collide with you if (oldCap >= MAXIMUM_CAPACITY) { //Modify the threshold to int Maximum value of threshold = Integer.MAX_VALUE; return oldTab; } /* If the maximum value is not exceeded, it will be expanded to twice the original value 1)(newCap = oldCap << 1) < MAXIMUM_CAPACITY After 2x expansion, the capacity should be less than the maximum capacity 2)oldCap >= DEFAULT_INITIAL_CAPACITY The original array length is greater than or equal to the array initialization length 16 */ else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY && oldCap >= DEFAULT_INITIAL_CAPACITY) //Double the threshold newThr = oldThr << 1; // double threshold } //Direct assignment when the old threshold point is greater than 0 else if (oldThr > 0) // The old threshold is assigned to the new array length newCap = oldThr; else {// Use defaults directly newCap = DEFAULT_INITIAL_CAPACITY;//16 newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY); } // Calculate new resize Maximum upper limit if (newThr == 0) { float ft = (float)newCap * loadFactor; newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ? (int)ft : Integer.MAX_VALUE); } //The default value of the new threshold is 12 times 2 and then becomes 24 threshold = newThr; //Create a new hash table @SuppressWarnings({"rawtypes","unchecked"}) //newCap Is the new array length-->32 Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; table = newTab; //Determine whether the old array is equal to null if (oldTab != null) { // Put each bucket All moved to new buckets in //Traverse each bucket of the old hash table and recalculate the new position of the elements in the bucket for (int j = 0; j < oldCap; ++j) { Node<K,V> e; if ((e = oldTab[j]) != null) { //The original data is assigned as null easy GC recovery oldTab[j] = null; //Determines whether the array has a next reference if (e.next == null) //There is no next reference, indicating that it is not a linked list. There is only one key value pair on the current bucket, which can be inserted directly newTab[e.hash & (newCap - 1)] = e; //Judge whether it is a red black tree else if (e instanceof TreeNode) //If the description is a red black tree to handle conflicts, call relevant methods to separate the trees ((TreeNode<K,V>)e).split(this, newTab, j, oldCap); else { // Using linked list to deal with conflicts Node<K,V> loHead = null, loTail = null; Node<K,V> hiHead = null, hiTail = null; Node<K,V> next; //Calculate the new position of the node through the principle explained above do { // Original index next = e.next; //Let's judge here if equal to true e This node is in resize There is no need to move the position later if ((e.hash & oldCap) == 0) { if (loTail == null) loHead = e; else loTail.next = e; loTail = e; } // Original index+oldCap else { if (hiTail == null) hiHead = e; else hiTail.next = e; hiTail = e; } } while ((e = next) != null); // Original cable lead bucket in if (loTail != null) { loTail.next = null; newTab[j] = loHead; } // Original index+oldCap put to bucket in if (hiTail != null) { hiTail.next = null; newTab[j + oldCap] = hiHead; } } } } } return newTab; }
4.3.4 delete method (remove)
After understanding the put method, the remove method is no longer difficult, so the repeated content will not be introduced in detail.
To delete, first find the location of the element. If it is a linked list, traverse the linked list to find the element and then delete it. If it is a red black tree, traverse the tree, and then delete it after finding it. When the tree is less than 6, turn the linked list.
remove method:
//remove The specific implementation of the method is removeNode Method, so let's focus on it removeNode method public V remove(Object key) { Node<K,V> e; return (e = removeNode(hash(key), key, null, false, true)) == null ? null : e.value; }
removeNode method:
final Node<K,V> removeNode(int hash, Object key, Object value, boolean matchValue, boolean movable) { Node<K,V>[] tab; Node<K,V> p; int n, index; //according to hash Find location //If current key The bucket mapped to is not empty if ((tab = table) != null && (n = tab.length) > 0 && (p = tab[index = (n - 1) & hash]) != null) { Node<K,V> node = null, e; K k; V v; //If the node on the bucket is what you're looking for key,Will node Point to this node if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))) node = p; else if ((e = p.next) != null) { //Indicates that the node has a next node if (p instanceof TreeNode) //Note: if the conflict is handled by the red black tree, obtain the node to be deleted by the red black tree node = ((TreeNode<K,V>)p).getTreeNode(hash, key); else { //Determine whether to process by linked list hash Conflict, if yes, search for the node to be deleted by traversing the linked list do { if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) { node = e; break; } p = e; } while ((e = e.next) != null); } } //Compare found key of value Match with the to be deleted if (node != null && (!matchValue || (v = node.value) == value || (value != null && value.equals(v)))) { //Delete the node by calling the method of red black tree if (node instanceof TreeNode) ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable); else if (node == p) //Linked list deletion tab[index] = node.next; else p.next = node.next; //Record modification times ++modCount; //Number of changes --size; afterNodeRemoval(node); return node; } } return null; }
4.3.5 find element method (get)
Find the method to find the Value through the Key of the element.
The code is as follows:
public V get(Object key) { Node<K,V> e; return (e = getNode(hash(key), key)) == null ? null : e.value; }
The get method mainly calls the getNode method. The code is as follows:
final Node<K,V> getNode(int hash, Object key) { Node<K,V>[] tab; Node<K,V> first, e; int n; K k; //If the hash table is not empty and key The corresponding bucket is not empty if ((tab = table) != null && (n = tab.length) > 0 && (first = tab[(n - 1) & hash]) != null) { /* Determine whether the array elements are equal Check the first element according to the position of the index Note: always check the first element */ if (first.hash == hash && // always check first node ((k = first.key) == key || (key != null && key.equals(k)))) return first; // If it is not the first element, judge whether there are subsequent nodes if ((e = first.next) != null) { // Judge whether it is a red black tree. If yes, call the in the red black tree getTreeNode Method to get the node if (first instanceof TreeNode) return ((TreeNode<K,V>)first).getTreeNode(hash, key); do { // If it's not a red black tree, it's a linked list structure. Judge whether the link exists in the linked list by circular method key if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) return e; } while ((e = e.next) != null); } } return null; }
Summary:
1. Implementation steps of get method:
1) Get the bucket to which the key is mapped through the hash value
2) If the key on the bucket is the key to be found, it will be found and returned directly
3) If the key on the bucket is not the key to be found, view the subsequent nodes:
- If the subsequent node is a red black tree node, get the value according to the key by calling the red black tree method
- If the subsequent node is a linked list node, the value is obtained by looping through the linked list according to the key
2. The above red black tree node calls the getTreeNode method to find through the find method of the tree node:
final TreeNode<K,V> getTreeNode(int h, Object k) { return ((parent != null) ? root() : this).find(h, k, null); } final TreeNode<K,V> find(int h, Object k, Class<?> kc) { TreeNode<K,V> p = this; do { int ph, dir; K pk; TreeNode<K,V> pl = p.left, pr = p.right, q; if ((ph = p.hash) > h) p = pl; else if (ph < h) p = pr; else if ((pk = p.key) == k || (k != null && k.equals(pk))) return p;//Return directly after finding else if (pl == null) p = pr; else if (pr == null) p = pl; else if ((kc != null || (kc = comparableClassFor(k)) != null) && (dir = compareComparables(kc, k, pk)) != 0) p = (dir < 0) ? pl : pr; //recursive lookup else if ((q = pr.find(h, k, kc)) != null) return q; else p = pl; } while (p != null); return null;
3. To find a red black tree, since the tree has been guaranteed to be orderly when added before, the search is basically a half search, which is more efficient.
4. Here, as during insertion, if the hash value of the comparison node is equal to the hash value to be found, it will judge whether the key s are equal, and if they are equal, they will be returned directly. If they are not equal, they are found recursively from the subtree.
5.
- If it is a tree, search through key.equals(k) in the tree, O(logn)
- If it is a linked list, search through key.equals(k) in the linked list, O(n).
4.3.6 several ways to traverse the HashMap set
1. Traverse Key and Values respectively
private static void method(HashMap<String, Integer> hm) { //Get all key Set<String> keys = hm.keySet(); for (String key : keys) { System.out.println(key); } //Get all value Collection<Integer> values = hm.values(); for (Integer value : values) { System.out.println(value); } }
2. Iterate using Iterator
private static void method_1(HashMap<String, Integer> hm) { Set<Map.Entry<String, Integer>> entries = hm.entrySet(); for(Iterator<Map.Entry<String, Integer>> it = entries.iterator();it.hasNext();){ Map.Entry<String, Integer> entry = it.next(); System.out.println(entry.getKey()+"---"+entry.getValue()); } }
3. get (not recommended)
private static void method_2(HashMap<String, Integer> hm) { Set<String> keys = hm.keySet(); for (String key : keys) { Integer value = hm.get(key); System.out.println(key+"---"+value); } }
Note: according to the Alibaba development manual, this method is not recommended because it iterates twice. The keySet obtains the Iterator once, and iterates again through get. Reduce performance.
4.jdk8 later, use the default method in the Map interface:
default void forEach(BiConsumer<? super K,? super V> action) BiConsumer Methods in the interface: void accept•(T t, U u) Perform this operation on the given parameter. parameter t - First input parameter u - Second input parameter
Traversal Code:
private static void method_3(HashMap<String, Integer> hm) { hm.forEach((key,value)->System.out.println(key+"---"+value)); }
Chapter 5 how to design multiple non duplicate key value pairs to store the initialization of HashMap?
5.1 HashMap initialization problem description
If we know exactly how many key value pairs we need to store, we should specify its capacity when initializing HashMap to prevent automatic capacity expansion of HashMap and affect the use efficiency.
By default, the capacity of HashMap is 16. However, if the user specifies a number as the capacity through the constructor, Hash will select a power greater than the first 2 of the number as the capacity. (3 - > 4, 7 - > 8, 9 - > 16). We have explained this above.
Alibaba Java development manual suggests that we set the initialization capacity of HashMap.

So why do you suggest that? Have you thought about it.
Of course, the above suggestions also have theoretical support. As described above, the capacity expansion mechanism of HashMap is to expand the capacity when the capacity expansion conditions are met. The capacity expansion condition of HashMap is that when the number (size) of elements in HashMap exceeds the threshold, it will be expanded automatically. In HashMap, threshold = loadFactor * capacity.
Therefore, if we do not set the initial capacity, HashMap may be expanded many times with the continuous increase of elements. The capacity expansion mechanism in HashMap determines that the hash table needs to be rebuilt for each capacity expansion, which greatly affects the performance.
However, setting the initialization capacity and different values will also affect the performance. When we know the number of KV to be stored in HashMap, how much should we set the capacity?
5.2 initialization of capacity in HashMap
When we use HashMap(int initialCapacity) to initialize the capacity, jdk will help us calculate a relatively reasonable value as the initial capacity by default. So, do we just need to pass the number of elements to be stored in the known HashMap directly to initialCapacity?
For the setting of this value, the following suggestions are made in Alibaba Java Development Manual:

In other words, if the default value we set is 7, it will be set to 8 after Jdk processing. However, this HashMap will be expanded when the number of elements reaches 8 * 0.75 = 6, which is obviously something we don't want to see. We should minimize the expansion. The reason has also been analyzed.
If we calculate through initialCapacity/ 0.75F + 1.0F, 7 / 0.75 + 1 = 10, 10 will be set to 16 after Jdk processing, which greatly reduces the probability of capacity expansion.
When the hash table maintained in HashMap reaches 75% (by default), rehash will be triggered, and the rehash process is time-consuming. Therefore, if the initialization capacity is set to initialCapacity/0.75 + 1, it can effectively reduce conflicts and errors.
Therefore, I can think that when we know the number of elements in the HashMap, setting the default capacity to initialCapacity/ 0.75F + 1.0F is a relatively good choice in performance, but it will also sacrifice some memory.
When we want to create a HashMap in the code, if we know the number of elements to be stored in the Map, setting the initial capacity of the HashMap can improve the efficiency to a certain extent.
However, the JDK does not directly take the number passed in by the user as the default capacity, but will perform some operation and finally get a power of 2. The reason has also been analyzed.
However, in order to avoid the performance consumption caused by capacity expansion to the greatest extent, we suggest that the default capacity can be set to initialCapacity/ 0.75F + 1.0F.