When we practice Java algorithm, we will inevitably encounter some problems. Using some skilled problem-solving methods is much better than not using them. This time, we mainly share the skills about double needles.

Double pointers are generally divided into two categories: one is fast and slow pointers, and the other is left and right pointers. The former mainly solves the problems in the linked list, such as the typical judgment of whether the linked list contains rings; The latter mainly solves the problems in arrays (or strings), such as binary search.

1, Speed pointer

1. Judge whether the linked list contains rings

If the linked list does not contain rings, the pointer will eventually encounter a null pointer. Null indicates that the linked list has reached the end. It's easy to say that the linked list does not contain rings

boolean hasCycle(ListNode head) {
    while (head != null) {
        head = head.next;
    }
    return false;
}

If there are rings in the linked list, the above code will fall into an endless loop, because there is no null pointer as the tail node in the ring array.

The classic solution is to use two pointers, one fast and the other slow. If there is no ring, the fast pointer will eventually encounter null, indicating that the linked list does not contain a ring. If the fast pointer eventually exceeds the full pointer by one circle and meets the slow pointer, it indicates that the linked list contains rings.

boolean hasCycle(ListNode head) {
    ListNode fast = head, slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        // If two pointers meet, it indicates that they form a ring and return true
        if (fast = slow) {
            return true;
        }
    }
    return false;
}

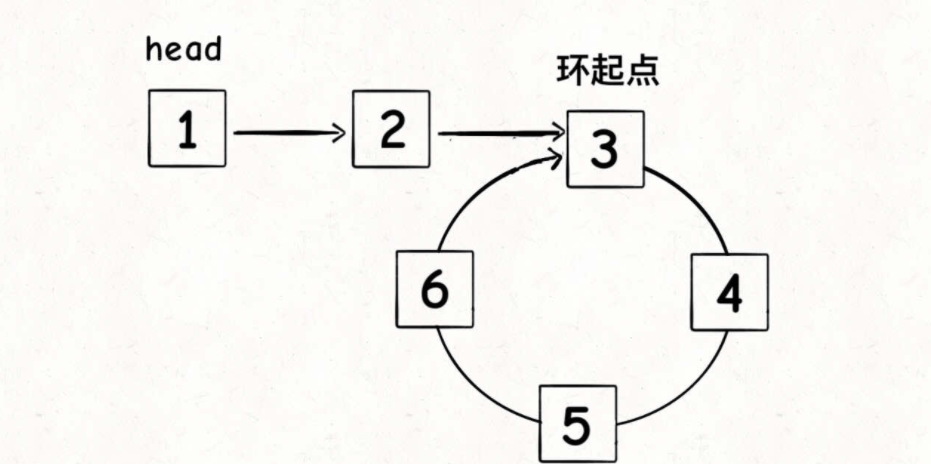
2. If it is known that the linked list contains a ring, return to the start and end position of the ring

ListNode detectCycle(ListNode head) {
    ListNode fast = head, slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (slow = fast) {
            break;
        }
    }
    if (fast == null || fast.next == null) {
        // fast did not encounter a ring and encountered a null pointer
        return null;
    }
    slow = head;
    while (slow != fast) {
        slow = slow.next;
        fast = fast.next;
    }
    return slow;
}

When the fast and slow pointers meet, let one of the pointers point to the head node, and then let the fast and slow pointers move forward at the same speed. When they meet again, it is the starting position of the ring.

Explanation:

In the first encounter, if the slow pointer slow takes k steps, then the fast pointer fast must take 2k steps;

Fast must have taken k steps more than slow. In fact, the extra k steps are that the fast pointer turns around in the ring, so the value of k is an integer multiple of the length of the ring.

Assuming that the distance between the meeting point and the starting point of the ring is m, the distance between the starting point of the ring and the head node is k - m, that is, if you advance K - M steps from the head, you can reach the starting point of the ring.

Coincidentally, if you continue to move k - m steps from the meeting point, you also happen to reach the starting point of the ring. Regardless of how fast turns in the ring and takes k steps to the meeting point, you must have reached the starting point of the ring by taking k - m steps

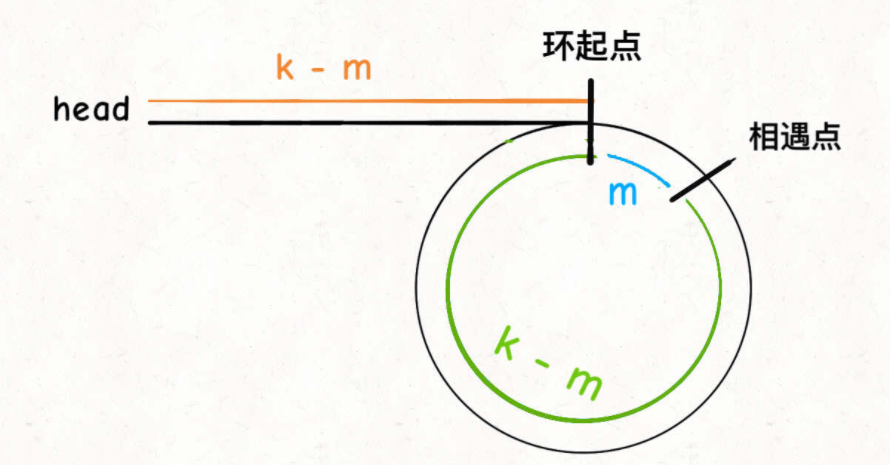
Therefore, as long as we re point any of the fast and slow pointers to head, and then the two pointers move forward at the same speed, k - m steps will meet, and the place where they meet is the starting point of the ring.

2, Left and right pointer

The left and right pointers in the array actually refer to two index values, which are generally initialized as left = 0 and right = num length - 1

1. Binary search

int binarySearch(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = (right + left) / 2;
     	if (nums[mid] == target) {
            return mid;
        }
        if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] < target) {
            left = mid + 1;
        }
    }
    return - 1;
}

2. Sum of two numbers

As long as the array is ordered, we should think of the double pointer technique,

int[] twoSum(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left < right) {
        int sum = nums[left] + nums[right];
        if (sum == target) {
            return new int[]{left, right}
        } else if (sum < target) {
            // Make sum bigger
            left++;
        } else if (sum > target) {
            // Make sum smaller
            right--;
        }
    }
    return new int[]{-1, -1};
}

3. Array inversion

Inverts an array of strings of type char []

void reverseString(char[] arr) {
    int left = 0, right = arr.length - 1;
    while (left <= right) {
        arr[left] = arr[left] + arr[right];
        arr[right] = arr[left] - arr[right];
        arr[left] = arr[left] - arr[right];
        left++;
        right--;
    }
}

If these examples can be mastered, then the basic ideas of double pointers and basic operations such as linked lists can be mastered. After mastering the basic skills, we still need to polish some topics. Writing more topics will be more deeply understood.