Problems with direct insertion sorting:
When the number of insertions behind is small, the number of backward shifts of the elements arranged in front will increase significantly, which has an impact on efficiency.
Sorting:
Improvement on the basis of direct insertion sort is also called reduced incremental sort.
Basic ideas:
Hill sorting is grouping the records according to a certain increment of the subscript, sorting each group by using the direct insertion sort algorithm; with the increment decreasing, each group contains more and more keywords, and when the increment is reduced to 1, the whole element set is divided into a set, and the algorithm terminates.

Dynamic diagrams: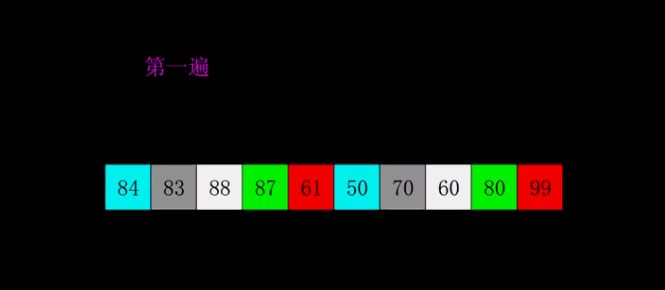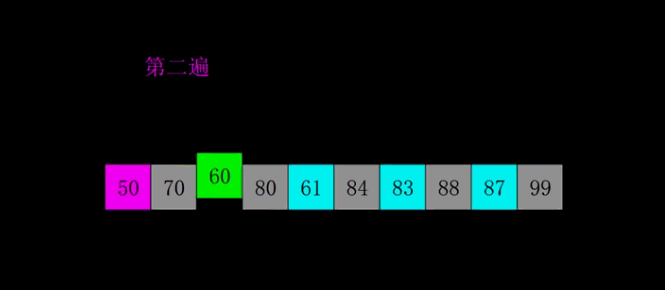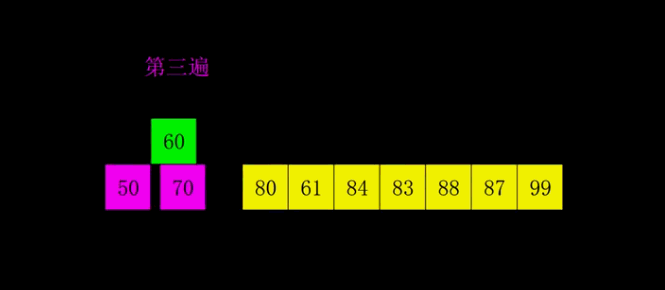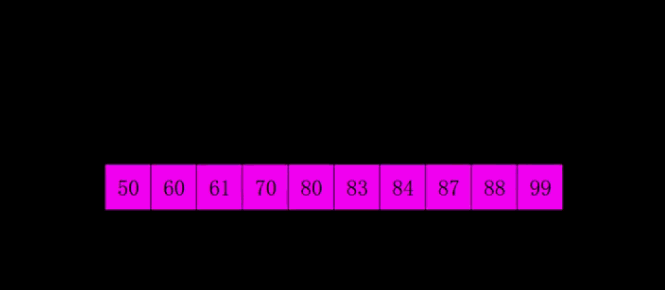

Java code implementation:

import java.util.Scanner;

public class Shell_sort {

//Sorting is an unstable sorting algorithm.

//Basic ideas:
//First, take an integer d1 less than n as the first increment, and group all the data. All records with multiple distances of d1 are placed in the same group. Firstly, insert and sort directly in each group.
//Then, take the second increment D2 < D1 to repeat the above grouping and sorting. Until the increment d=1, i.e., all records are placed in the same group for direct insertion sort
//Generally, half of the initial sequence is incremental, and then halves each time until the increment is 1.

public static void main(String[] args) {
	// TODO Auto-generated method stub
	System.out.println("Enter the size of the array:");
	Scanner input = new Scanner(System.in);
	int a = input.nextInt();
	int [] arr = new int[a];
	for(int i = 0;i<arr.length;i++) {
		System.out.println("Please enter the number of arrays"+i+"Value:");
		int s = input.nextInt();
		arr[i] = s;
	}
	arr = HillSort(arr);
	for(int i = 0;i<arr.length;i++)
	System.out.print(" "+arr[i]+" ");
}
public static int[] HillSort(int[] arr) {
	//Take out the length of the array separately to improve efficiency
	int length = arr.length;
	//If the intercepted length is not 1, it will be calculated all the time.
	while(length!=0) {
		//Integration, equal to the number of elements in each group
		length = length/2;
		//The number of elements in each group is repeated several times.
		for(int i =0;i<length;i++) {
			int tem = arr[i];
			//Grouping elements
			for(int j = i+length;j<arr.length;j+=length) {
				//The value of k is an array subscript for the last value of each group.
				int k = j-length;
				//Assign each number to be inserted to an intermediate variable
				int temp = arr[j];
				//Compare this number, and if it is smaller than the ordered array, the array moves backwards.
				while(k>=0&&temp<arr[k]) {
					//Corresponding Elements Move Back
					arr[k+length] = arr[k];
					//Corresponding subscript forward
					k-= length;
				}
				//Find the location of elements not less than the ordered array and insert them
				arr[k+length] = temp;
			}
		}
	}
	return arr;
	
	}
}