3, Array

1. Concept of array

Array: an array is a collection of multiple data of the same type arranged in a certain order, named with a name, and managed uniformly by numbering.

Common concepts of arrays:

• Array name
• Subscript (index)
• element
• Length of array

Array features:

1. The array is arranged in order.

2. The array is a reference type variable. The element of an array can be either a basic data type or a reference data type.

3. Creating an array object will open up a whole block of continuous memory space in memory.

4. Once the length of the array is determined, it cannot be modified

Classification of arrays:

① By dimension: one dimensional array, two-dimensional array, three-dimensional array

②   According to the data type of the element, it is divided into: array of basic data type elements and array of reference data type elements (i.e. object array)

2. Use of one-dimensional arrays

① Declaration and initialization of one-dimensional array
  ② How to call an element at a specified position in an array
  ③ How to get the length of an array
  ④ How to traverse an array
  ⑤ Default initialization value for array elements  
   ⑥ Memory analysis of array  

(1) Declaration and initialization of one-dimensional array

Statement:  

  type[]   var   Or type var []

For example: int a []     String[]   str

When declaring an array in the Java language, its length (the number of elements in the array) cannot be specified, for example: int a[5]// illegal

initialization:

①   Static initialization: array initialization and array assignment are performed simultaneously

a = new int[] {1001,1002,1003};

String[] b = new String[]{"aa","bb","cc"};

②   Dynamic initialization: array initialization and array assignment are performed separately

String[] names = new String[5];

(2) Reference to element

Each element in the array can be referenced only after defining and allocating space for it with the operator new;

Reference method of array element: array name [array element subscript]

• Array element subscripts can be integer constants or integer expressions. Such as a [3], B [i], C [6 * I]
• Array element subscript starts from 0; Legal subscript value range of array with length n: 0 - > n-1; For example, int a[]=new int[3]; The array elements that can be referenced are a[0], a[1], a[2]

(3) Get array length

Each array has an attribute length indicating its length. For example, a.length indicates the length of array a (number of elements)

• Once an array is initialized, its length is immutable

(4) One dimensional array traversal

for(int i = 0;i < array.length;i++) {
            System.out.println(array[i]);
    }

(5) Default initialization value of one-dimensional array

• Array element is an integer: 0   ( byte,short,int,long)
• Array elements are floating point: 0.0  
• Array elements are char type: 0 or 'u0000', not '0'
•   Array elements are boolean: false     0   one
•   Array element is a reference type: null

(6) Memory parsing of arrays

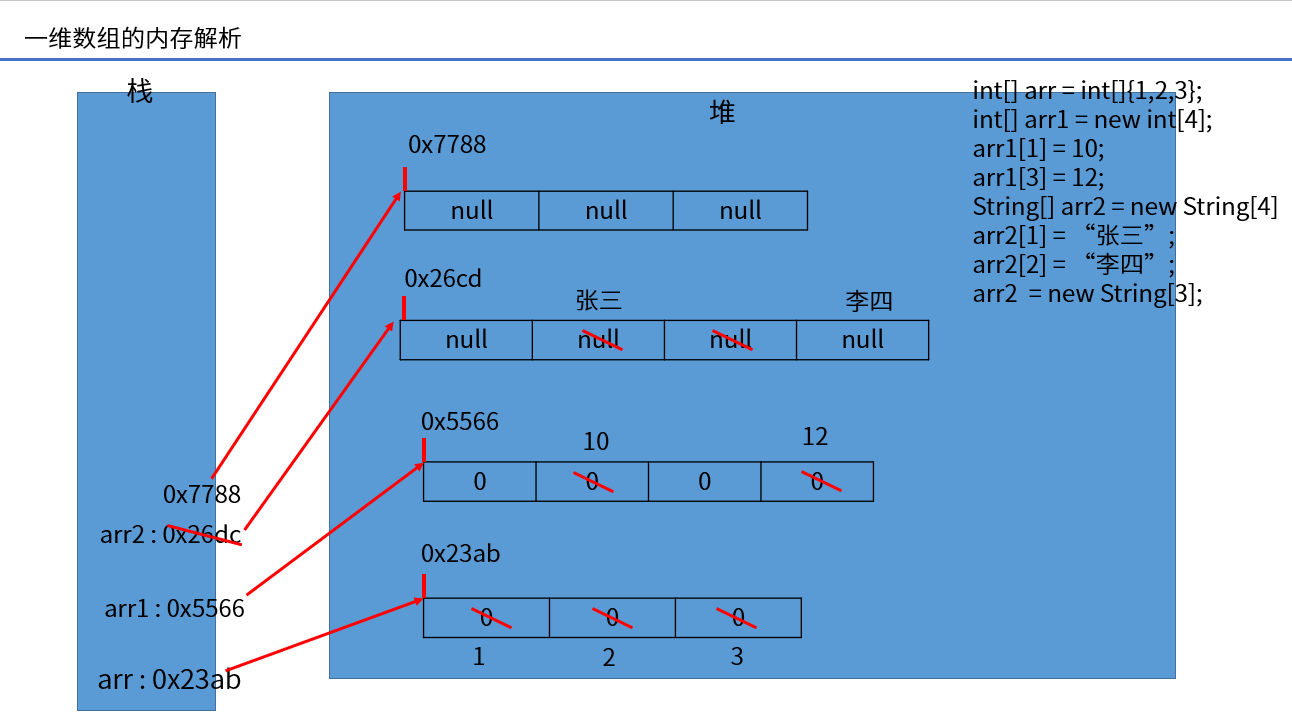
  Exercise:

Read the student's grades from the keyboard, find out the highest score, and output the student's grade.

Score > = highest score - 10, grade 'A'

Score > = highest score - 20, grade 'B'

Score > = highest score - 30, grade 'C'

rest                      Grade'D '

Tip: first read in the number of students, create an int array according to the number of students, and store the student scores.

import java.util.Scanner;

public class ArrayExer1 {

	public static void main(String[] args) {
		
		//1. Use Scanner to receive data
		Scanner scan = new Scanner(System.in);
		System.out.println("Please enter the number of students:");
		int num = scan.nextInt();
		
		
		//2. Use an array to store student scores: dynamic initialization
		int[] scores = new int[num];
		//3. Assign values to the elements in the array
		System.out.println("Please enter" + num + "Student grades");
		for(int i = 0;i < scores.length;i++) {
			scores[i] = scan.nextInt();
		}
		//4. Get the maximum value in the array
		int maxScore = 0;
		for(int i = 0;i < scores.length;i++) {
			if(maxScore < scores[i]) {
				maxScore = scores[i];
			}
		}
		System.out.println("The highest score is:" + maxScore);
		//5. According to the difference between each student and the highest score, get the grade of each student, and output the score and grade
		char level;
		for(int i = 0;i < scores.length;i++) {
			if(maxScore - scores[i] <= 10) {
				level = 'A';
			}else if(maxScore - scores[i] <= 20) {
				level = 'B';
			}else if(maxScore - scores[i] <= 30) {
				level = 'C';
			}else {
				level = 'D';
			}
			System.out.println("student " + i + " score is " + scores[i] + " grade is " + level);
			
		}
		
	}
}

3. Two dimensional array

For the understanding of two-dimensional array, we can see that one-dimensional array array1 exists as an element of another one-dimensional array array2. In fact, from the perspective of the underlying operation mechanism of the array, there is no multidimensional array.

Use of 2D arrays:
  ① Declaration and initialization of two-dimensional array
  ② How to call an element at a specified position of an array
  ③ How to get the length of an array
  ④ How to traverse an array
  ⑤ Default initialization value for array elements
  ⑥ Memory parsing of arrays  

(1) Declaration and initialization

//Static initialization
int[][] arr1 = new int[][] {{1,2,3},{4,5},{7,8,9}};
//Dynamic initialization 1
String[][] arr2 = new String[3][2];
//Dynamic initialization 2
String[][] arr3 = new String[3][];

(2) Call

System.out.println(arr1[0][1]);//2
System.out.println(arr2[1][1]);//null

arr3[1] = new String[4];
System.out.println(arr3[1][0]);
System.out.println(arr3[0]);//

(3) Traversal and length properties

 for(int i = 0;i < arr.length;i++){
            for(int j = 0;j < arr[i].length;j++) {
                System.out.print(arr[i][j] + " ");
            }
            System.out.println();
 }

 ( 4) Default initialization value for 2D array

   Use of 2D arrays:
           Regulation: the two-dimensional array is divided into the elements of the outer array and the elements of the inner array
                 int[][] arr = new int[4][3];
                 Outer array: arr[0],arr[1]
                 Inner array: arr[0][0],arr[1][2]
 
Default initialization values for array elements:
    For initialization method 1: for example, int[][] arr = new arr[4][3];
        The initialization value of the outer element is: address value
        The initialization value of the inner element is: the same as the one-dimensional array

    For initialization mode 2: for example: int[][] arr = new arr[4] [];
        The initialization value of the outer element is null
        The initialization value of the inner element is: it cannot be called, otherwise an error is reported

(5) Memory parsing of arrays

 

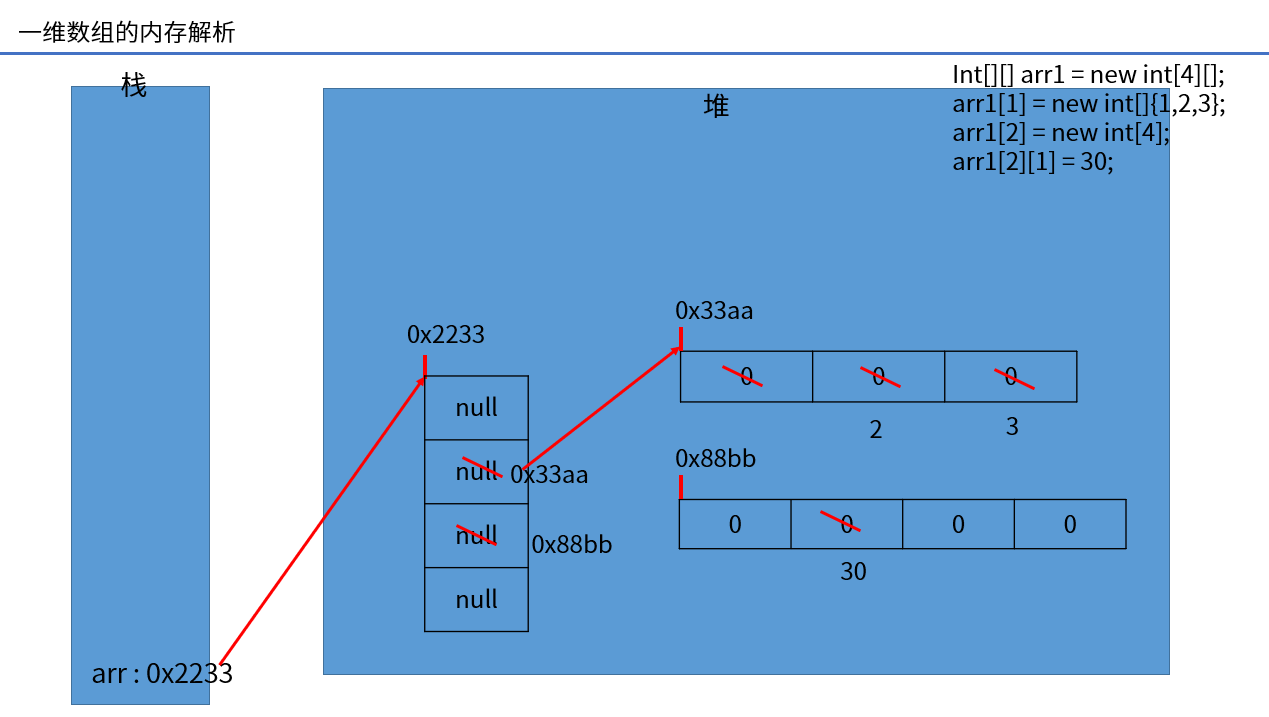
  Exercise:

1.

 

/*
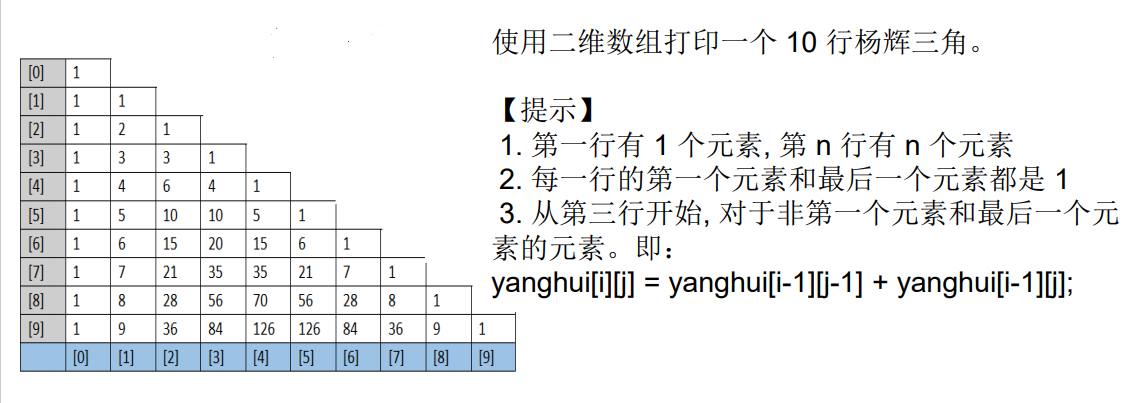
 * Print 10 lines Yang Hui triangle
 */
public class YangHuiTest {

	public static void main(String[] args) {
		//1. Declare and initialize a two-dimensional array
		int[][] yangHui = new int[10][];
		//2. Assign values to the elements of the array
		for(int i = 0;i < yangHui.length;i++) {
			
			yangHui[i] = new int[i+1];
			//2.1. Assign values to the first and last elements
			yangHui[i][0] = yangHui[i][i] = 1;
			//2.2. Assign values to non first and last elements of each line
			if(i > 1) {
				for(int j = 1;j < yangHui[i].length - 1;j++) {
					yangHui[i][j] = yangHui[i-1][j] + yangHui[i-1][j-1];
				}
			}		
		}
		//3. Traversal array
		for(int i = 0;i < yangHui.length;i++) {
			for(int j = 0;j < yangHui[i].length;j++) {
				System.out.print(yangHui[i][j] +" ");
			}
			System.out.println();
		}
	}
}

  2. Create an int array with a length of 6. The values of array elements are required to be between 1-30 and assigned randomly. At the same time, the values of the required elements are different.

/*
 * Create an int array with a length of 6. The values of array elements are required to be between 1-30 and assigned randomly. At the same time, requirements
 *  Elements have different values.
 */
public class ArrayExer1 {

	public static void main(String[] args) {
		//Mode 1:
		
//		//1. Create a one-dimensional array
//		int[] arr = new int[6];
//		//2. Assign a value to the array
//		for(int i = 0;i < arr.length;i++) {
//			//2.1. Obtain a random number of 1-30 [0,1] [0,30) [1,31)
//			//Remember to add parentheses, or perform the cast first, which is always 0
//			arr[i] = (int)(Math.random()*30) + 1;
//			//3. Judge whether the elements are the same
//			boolean isFlag = false;
//			while(true) {
//				for(int j = 0;j < i;j++) {
//					
//					if(arr[i] == arr[j]) {
//						isFlag = true;
//						break;
//					}
//				}
//				//4. If the same, re assign the value
//				if(isFlag) {
//					arr[i] = (int)(Math.random()*30) + 1;
//					//Don't forget to reinitialize
//					isFlag = false;
//					continue;
//				}
//				//Jump out of while loop
//				break;
//			}
//			
//		}
//		//Traversal array
//		for(int i = 0;i < arr.length;i++) {
//			System.out.print(arr[i] + " ");
//		}
		
		//Mode 2:
		
		//1. Create a one-dimensional array
		int[] arr = new int[6];
		//2. Assign a value to the array
		for(int i = 0;i < arr.length;i++) {
			//2.1. Obtain a random number of 1-30 [0,1] [0,30) [1,31)
			//Remember to add parentheses, or perform the cast first, which is always 0
			arr[i] = (int)(Math.random()*30) + 1;
			//3. Judge whether the elements are the same
				for(int j = 0;j < i;j++) {
					
					if(arr[i] == arr[j]) {
						i--;
						continue;
					}
				}
			
		}
		//Traversal array
		for(int i = 0;i < arr.length;i++) {
			System.out.print(arr[i] + " ");
		}
		
	}
}

3. Implementation of square matrix of loop number format

Enter an integer (1 ~ 20) from the keyboard  

Then take this number as the size of the matrix and put 1,2,3... n*n   The number of is filled in as a clockwise spiral. For example:   Enter the number 2 and the program outputs:   one   two  

                                4 3 

Enter the number 3 and the program outputs:   one   two   three  

                                           8 9 4 

                                           7 6 5 

Enter the number 4,   Program output:  

1   2   3   4 

12  13  14  5 

11  16  15  6 

10   9  8    7

Mode 1:
class RectangleTest {
	public static void main(String[] args) {
		Scanner scanner = new Scanner(System.in);
		System.out.println("Enter a number");
		int len = scanner.nextInt();
		int[][] arr = new int[len][len];

		int s = len * len;
		/*
		 * k = 1:Right k = 2: down k = 3: left k = 4: up
		 */
		int k = 1;
		int i = 0, j = 0;
		for (int m = 1; m <= s; m++) {
			if (k == 1) {
				if (j < len && arr[i][j] == 0) {
					arr[i][j++] = m;
				} else {
					k = 2;
					i++;
					j--;
					m--;
				}
			} else if (k == 2) {
				if (i < len && arr[i][j] == 0) {
					arr[i++][j] = m;
				} else {
					k = 3;
					i--;
					j--;
					m--;
				}
			} else if (k == 3) {
				if (j >= 0 && arr[i][j] == 0) {
					arr[i][j--] = m;
				} else {
					k = 4;
					i--;
					j++;
					m--;
				}
			} else if (k == 4) {
				if (i >= 0 && arr[i][j] == 0) {
					arr[i--][j] = m;
				} else {
					k = 1;
					i++;
					j++;
					m--;
				}
			}
		}

		// ergodic
		for (int m = 0; m < arr.length; m++) {
			for (int n = 0; n < arr[m].length; n++) {
				System.out.print(arr[m][n] + "\t");
			}
			System.out.println();
		}
	}
}

Mode 2:
class RectangleTest1 {

	public static void main(String[] args) {
		int n = 7;
		int[][] arr = new int[n][n];

		int count = 0; // Data to display
		int maxX = n - 1; // Maximum subscript of x axis
		int maxY = n - 1; // Maximum subscript of Y axis
		int minX = 0; // Minimum subscript of x axis
		int minY = 0; // Minimum subscript of Y axis
		while (minX <= maxX) {
			for (int x = minX; x <= maxX; x++) {
				arr[minY][x] = ++count;
			}
			minY++;
			for (int y = minY; y <= maxY; y++) {
				arr[y][maxX] = ++count;
			}
			maxX--;
			for (int x = maxX; x >= minX; x--) {
				arr[maxY][x] = ++count;
			}
			maxY--;
			for (int y = maxY; y >= minY; y--) {
				arr[y][minX] = ++count;
			}
			minX++;
		}

		for (int i = 0; i < arr.length; i++) {
			for (int j = 0; j < arr.length; j++) {
				String space = (arr[i][j] + "").length() == 1 ? "0" : "";
				System.out.print(space + arr[i][j] + " ");
			}
			System.out.println();
		}
	}
}

4. Common algorithms involved in arrays

1. Assignment of array elements (Yang Hui triangle, loop number, etc.)

2. Find the maximum, minimum, average, sum, etc. of the elements in the numerical array

3. Array copy, inversion and search (linear search, dichotomy search)

4. Sorting algorithm of array elements

2.

/*
 * Examination of the algorithm: find the maximum, minimum, average, sum, etc. of the elements in the numerical array
 * 
 * Define a one-dimensional array of int type, containing 10 elements, and assign some random integers respectively,
 * Then find the maximum, minimum, sum and average values of all elements and output them.
 * Requirement: all random numbers are two digits.
 * 
 */
public class ArrayTest1 {

	public static void main(String[] args) {

		int[] arr = new int[10];
		
		for(int i = 0;i < arr.length;i++) {
			arr[i] = (int)(Math.random()*90 + 10);
		}
		
		//Traversal output
		for(int i = 0;i < arr.length;i++) {
			System.out.print(arr[i] + " ");
		}
		
		System.out.println();
		//Maximum value in array
		int maxValue = arr[0];
		for(int i = 0;i < arr.length;i++) {
			if(maxValue < arr[i]) {
				maxValue = arr[i];
			}
		}
		System.out.println("The maximum value is:" + maxValue);
		
		//Array minimum
		int minValue = arr[0];
		for(int i = 0;i < arr.length;i++) {
			if(minValue > arr[i]) {
				minValue = arr[i];
			}
		}
		System.out.println("The minimum value is:" + minValue);
		
		//and
		int sum = 0;
		for(int i = 0;i < arr.length;i++) {
			sum += arr[i];
		}
		System.out.println("And values are:" + sum);
		
		//average value
		int averageValue = sum / 10;
		System.out.println(averageValue);
	}
}

3.

/*
 * Algorithm examination: array copy, inversion and search (linear search and dichotomy search)
 * 
 */
public class ArrayTest2 {

	public static void main(String[] args) {
		
		String[] arr = new String[] {"JJ","DD","MM","BB","GG","AA"};
		
		//Copy of array
		String[] arr1 = new String[arr.length];
		for(int i = 0;i < arr1.length;i++) {
			arr1[i] = arr[i];
		}
		
		//Inversion of arrays
		//Method 1:
//		for(int i = 0;i < arr.length / 2;i++) {
//			String temp = arr[i];
//			arr[i] = arr[arr.length-1-i];
//			arr[arr.length-1-i] = temp;
//		}
		
		//Method 2:
		for(int i=0,j=arr.length-1;i<j;i++) {
			String temp = arr[i];
			arr[i] = arr[j];
			arr[j] = temp;
		}
		
		for(int i = 0;i < arr.length;i++) {
			System.out.println(arr[i] + " ");
		}
		
		//Find (or search)
		//Linear search
		String dest = "BB";
		boolean flag = true;
		for(int i = 0;i < arr.length;i++) {
			if(dest.equals(arr[i])) {
				System.out.println("The specified element was found with index:" + i);
				flag = false;
				break;
			}
		}
		if(flag) {
			System.out.println("The specified element was not found");
		}
		
		//Dichotomy search: (familiar)
		//Premise: the array to be found must be ordered
		int[] arr3 = new int[]{-99,-54,-2,0,2,33,43,256,999};
		
		int number = 2561;//Element to find
		boolean flag1 = false;
		int head = 0;//First index position
		int end = arr3.length - 1;//Tail lead position
		while(head <= end) {
			int middle = (head + end) / 2; 
			
			if(arr3[middle] == number) {
				System.out.println("Found the specified element with index:" + middle);
				flag1 = true;
				break;
			}else if(arr3[middle] > number) {
				end = middle - 1;
			}else {//arr3[middle] < number
				head = middle + 1;
			}
		}
		
		if(flag1 == false) {
			System.out.println("The specified element was not found");
		}
		
	}
}

4. Sorting algorithm

Top ten internal sorting algorithms:

Select sort:

         Direct selection sorting and heap sorting

Swap sort:

         Bubble sort, quick sort

Insert sort:

        Direct insert sort, half insert sort, Shell sort

Merge sort

General sorting

Cardinality sort

  Bubble sorting

Introduction:

The principle of bubble sorting is very simple. It repeatedly visits the sequence to be sorted, compares two elements at a time, and exchanges them if their order is wrong.

Sorting idea:

1. Compare adjacent elements. If the first one is larger than the second (in ascending order), exchange them.

2. Do the same work for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end. After this step, the last element will be the maximum number.

3. Repeat the above steps for all elements except the last one.

4. Continue to repeat the above steps for fewer and fewer elements each time until there is no pair of numbers to compare.

/*
 * Implementation of array bubble sorting
 * 
 */
public class BubbleSortTest {

	public static void main(String[] args) {
		int[] arr = new int[] {43,32,76,-98,0,64,33,-21,32,99};
		
		for(int i = 0;i < arr.length - 1;i++) {//There's no need to compare the last number
			
			for(int j = 0;j < arr.length - 1 - i;j++) {
				if(arr[j] > arr[j+1]) {
					int temp = arr[j];
					arr[j] = arr[j+1];
					arr[j+1] = temp;
				}
			}
		}
		
		for(int i = 0;i < arr.length;i++) {
			System.out.println(arr[i] + " ");
		}
	}
}

Quick sort

Introduction:

Fast sorting is usually faster than other algorithms with the same name of O(nlogn), so it is often used. Moreover, fast sorting adopts the idea of divide and conquer, so we can often see the shadow of fast sorting in many written interviews. It can be seen that it is important to master fast platoon.

Quick Sort was invented by Tony Hoare, a Turing prize winner. It is listed as one of the top ten algorithms in the 20th century and the fastest of all internal sorting algorithms so far. Bubble sort upgrade, a kind of exchange sort. The time complexity of Quick Sort is O(nlog(n)).

Sorting idea:

1. Select an element from the sequence, which is called "pivot",

2. Reorder the sequence. All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark (the same number can be on either side). After the partition, the benchmark is in the middle of the sequence. This is called a partition operation.

3. Recursively sort the subsequence less than the reference value element and the subsequence greater than the reference value element.

4. The bottom case of recursion is that the size of the sequence is zero or one, that is, it has always been sorted. Although it recurses all the time, the algorithm will always end, because in each iteration, it will put at least one element to its last position.

/**
 * Quick sort
 * The records to be sorted are divided into two independent parts through one-time sorting. The keywords of some records are smaller than those of the other,
 * Then continue sorting the two parts respectively until the whole sequence is in order.
 */
public class QuickSort {
	private static void swap(int[] data, int i, int j) {
		int temp = data[i];
		data[i] = data[j];
		data[j] = temp;
	}

	private static void subSort(int[] data, int start, int end) {
		if (start < end) {
			int base = data[start];
			int low = start;
			int high = end + 1;
			while (true) {
				while (low < end && data[++low] - base <= 0)
					;
				while (high > start && data[--high] - base >= 0)
					;
				if (low < high) {
					swap(data, low, high);
				} else {
					break;
				}
			}
			swap(data, start, high);
			
			subSort(data, start, high - 1);//Recursive call
			subSort(data, high + 1, end);
		}
	}
	public static void quickSort(int[] data){
		subSort(data,0,data.length-1);
	}
	
	
	public static void main(String[] args) {
		int[] data = { 9, -16, 30, 23, -30, -49, 25, 21, 30 };
		System.out.println("Before sorting:\n" + java.util.Arrays.toString(data));
		quickSort(data);
		System.out.println("After sorting:\n" + java.util.Arrays.toString(data));
	}
}

5. Use of Arrays tool class

/*
 * 
 * java.util.Arrays: The tool class for operating arrays defines many methods for operating arrays
 */
public class ArraysTest {

	public static void main(String[] args) {
		
		//1.boolean equals(int[] a,int[] b) judge whether two arrays are equal
		int[] arr1 = new int[] {1,2,3,4};
		int[] arr2 = new int[] {1,3,4,2};
		boolean isEquals = Arrays.equals(arr1, arr2);
		System.out.println(isEquals);
		
		//2.String toString(int[] a) output array information any type of array
		System.out.println(Arrays.toString(arr1));
		String[] arr3 = new String[] {"Tom","LingLing","Jerry","DaMing"};
		System.out.println(Arrays.toString(arr3));
		
		//3.void fill(int[] a,int val) fills the specified value into the array
		Arrays.fill(arr1,10);
		System.out.println(Arrays.toString(arr1));
		
		//4.void sort(int[] a) sort the array
		Arrays.sort(arr2);
		System.out.println(Arrays.toString(arr2));
		 
		//5.int binarySearch(int[] a,int key) dichotomy the sorted array to retrieve the specified value
		int[] arr4 = new int[]{-98,-34,2,34,54,66,79,105,210,333};
		int index = Arrays.binarySearch(arr4, 105);
		if(index > 0) {
			System.out.println(index);
		}else {
			System.out.println("The specified element was not found");
		}
		
	}
}

6. Common exceptions in array usage

Common exceptions in arrays:

1. Array subscript out of bounds exception: ArrayIndexOutOfBoundsException

2. Null pointer exception: NullPointerException

public class ArrayExceptionTest {

	public static void main(String[] args) {
		
		//1. Array subscript out of bounds exception: ArrayIndexOutOfBoundsException
		int[] arr = new int[] {1,2,3,4,5};
		
//		for(int i = 0;i <= arr.length;i++) {
//			System.out.println(arr[i]);
//		}
		
//		System.out.println(arr[-2]);
		
		//Null pointer exception: NullPointerException
		//Case 1:
		int[] arr1 = new int[] {1,2,3};
		arr1 = null;
//		System.out.println(arr1[1]);
		
		//Case 2:
		int[][] arr2 = new int[4][];
//		System.out.println(arr2[2][0]);
		
		//Case 3:
		String[] arr3 = new String[] {"aa","bb","dd"};
		arr3[1] = null;
//		System.out.println(arr3[1].toString());
		System.out.println(arr3[2].toString());
	}
}