Insert sort

1. Insert sorting directly

Moving picture transfer gate.
Thought: when playing poker, uncover the cards one by one and find the insertion position from back to front, so that the cards in your hand are always in an orderly state

// 1. Direct insertion
public static void insertSort(int[] array) {
    // 1. Uncover the cards one by one, and the cards in hand have always been orderly
    for (int i = 1; i < array.length; i++) {
        // Uncover the i-th card
        int curNum = array[i];
        // 2. Look forward for a place to insert
        int j = i - 1;
        while (j >= 0 && curNum < array[j]) {
            // Before reaching the insertion position, move the j position backward to leave a space
            array[j + 1] = array[j];
            j --;
        }
        // 3. Insert the exposed card
        array[j + 1] = curNum;
    }
}

Time complexity:

Time complexity	Average: O(n^2)	Best (in order): O(n)	Worst case (in reverse order): O(n^2)

Space complexity: O(1)
Stability: stable
Optimization: search in half. First find the corresponding position of the team in half, and then move it

2. Hill sort

Illustration:

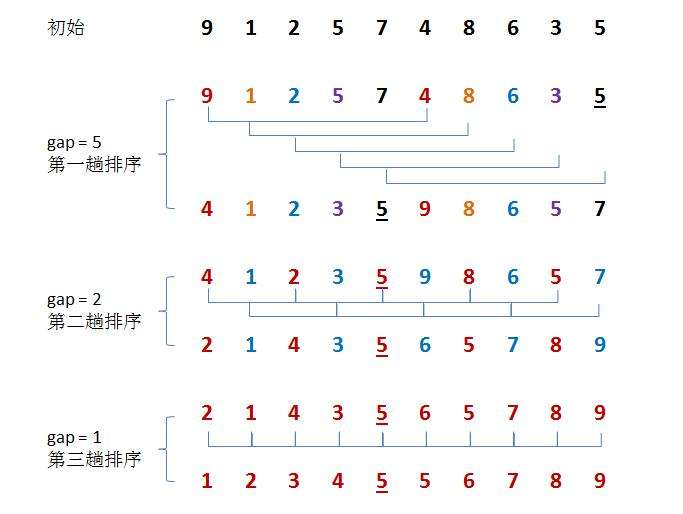
Idea: the time complexity of direct insertion sort is O(n) when it is ordered. The idea of Hill sort is to make the array tend to order first, and then carry out direct insertion sort.
Specific method: divide all the records with distance n in the array to be sorted into the same group, and sort the records in each group. In this way, the edges with a distance of N are in order. Then reduce the n value and repeat the above operations. The whole array gradually tends to be in order. Finally, when n = 1, it is directly inserted and sorted.

// 2. Hill sort
public static void shellSort(int[] array) {
    int gap = array.length;
    while (gap > 0) {
        insertSortGap(array, gap);
        // Reduced increment formula
        gap = gap /3 + 1;
    }
    // At this time, the array has become orderly. When gap = 1, it is equivalent to direct insertion sorting
    insertSortGap(array,1);
}

private static void insertSortGap(int[] array, int gap) {
    // Sort the number of gap s in the array, which is similar to direct insertion sorting
    for (int i = gap; i < array.length; i += gap) {
        int curNum = array[i];
        int j = i - gap;
        while (j >= 0 && curNum < array[j]) {
            array[j + gap] = array[j];
            j -= gap;
        }
        array[j + gap] = curNum;
    }
}

Time complexity:

Time complexity	Average: O(n^1.3)	Best: O(n)	Worst case: O(n^2)

Space complexity: O(1)
Stability: unstable

Select sort

3. Select Sorting directly

Idea: in each round, select the smallest number from the disordered interval and exchange it to the front

// 3. Select Sorting directly
public static void selectSort(int[] array) {
    // Select the smallest decimal from the unordered interval and exchange it to the front ordered interval of the unordered interval [0,i) unordered interval [i,len]
    for (int i = 0; i < array.length; i++) {
        int minIndex = i;
        // Find minimum subscript
        for (int j = i + 1; j < array.length; j++) {
            if (array[j] < array[minIndex]) {
                minIndex = j;
            }
        }
        // Once found, swap locations
        int tmp = array[i];
        array[i] = array[minIndex];
        array[minIndex] = tmp;
    }
}

Time complexity: each round should be traversed from beginning to end. It is not sensitive to data. O(n^2)
Space complexity: O(1)
Stability: unstable
Optimization: two-way selection sorting, finding the largest and smallest elements from the unordered interval each time and putting them at the top and last

4. Heap sorting

Animation demonstration.
Idea: it is the same as direct selection sorting, but instead of using each round of traversal to find the minimum number of unordered intervals to be placed at the front, it selects the maximum value (the number at the top of the heap) to be placed at the last side by creating a large root heap
Note: a lot should be built in ascending order; In descending order, small piles should be built

// 4. Stacking and discharging
public static void heapSort(int[] array) {
    // 1. Create a large root heap
    int end = array.length;
    for (int i = (end - 1) / 2; i >= 0 ; i--) {
        // Adjust downward from the last non cotyledon node
        adjustDown(array, i, end);
    }
    // 2. Select the maximum number of exchange positions
    while (end > 0) {
        // Change the maximum number to the last side
        swap(array, 0, end);
        // Reduce disordered interval
        end --;
        //Then adjust downward
        adjustDown(array, 0, end);
    }
}
// Adjust downward: adjust the value of the parent node to be greater than that of the child node. Compare and exchange with the parent node after finding the largest child node
private static void adjustDown(int[] array, int parent, int end) {
    // Default maximum child node
    int child = 2 * parent + 1;
    // The parent node that may need to be adjusted is a very small number. After exchanging with the largest child node, it is still smaller than the child node, so it needs to be adjusted. Therefore, the loop should be in the while loop until it is larger than the child node or there is no child node to end the loop
    while (child <= end) {
        // If there is a right child and the right child is greater than the left child, update the maximum child node
        if (child + 1 <= end && array[child + 1] > array[child]) {
            child += 1;
        }
        // At this time, the child is already the largest child node
        if (array[child] > array[parent]) {
            // If the largest child node is larger than the parent node, exchange
            swap(array, child, parent);
            // Start the next round of adjustment from the child node
            parent = child;
            child = 2 * parent + 1;
        } else {
            // Greater than child node, jump out of loop
            break;
        }
    }
}
// change of position
private static void swap(int[] array, int i, int j) {
    int temp = array[i];
    array[i] = array[j];
    array[j] = temp;
}

Time complexity: O(logn)
Space complexity: O(1)
Stability: unstable

Exchange sort

5. Bubble sorting

Idea: in the unordered interval, the largest number bubbles to the end of the unordered interval through the comparison of adjacent numbers

// 5. Bubble sorting
public static void bubbleSort(int[] array) {
    // Unordered interval [0, len-i], i represents the number of ordered intervals
    for (int i = 0; i < array.length; i++) {
        // Ergodic unordered interval
        for (int j = 0; j < array.length - i - 1; j++) {
            // Compare and exchange two adjacent numbers with larger numbers
            if (array[j] > array[j + 1]) {
            	// change of position
                int tmp = array[j];
                array[j] = array[j + 1];
                array[j + 1] = tmp;
            }
        }
    }
}

Time complexity: O(n^2)
Space complexity: O(1)
Stability: stable

6. Fast exhaust

Idea: select a number as the benchmark, make a round of traversal to determine the position of the benchmark (the position of the benchmark after the array is ordered), and ensure that all on the left are less than the benchmark and all on the right are greater than the benchmark, and then carry out the same operation on both sides of the benchmark. That is, the interval to be sorted is divided into two large and small intervals in each round, and the dividing point in the middle is the benchmark number.

// 6. Fast exhaust
public static void quickSort(int[] array) {
    quick(array, 0, array.length - 1);
}
// recursion
private static void quick(int[] array, int low, int high) {
    // End condition
    if (low >= high) return;
    // Determine the dividing point of the large and small intervals
    int piv = pivot(array, low, high);
    // Recursion on both sides of interval
    quick(array, low, piv);
    quick(array, piv + 1, high);
}
// Divide the size range and return the division point subscript
private static int pivot(int[] array, int start, int end) {
    // Determine the first place of the interval to be sorted as the benchmark number
    int piv = array[start];
    // Start looking for the location of the reference number
    while (start < end) {
        // Find the number less than the reference number from the right
        while (array[end] >= piv) {
            end --;
        }
        // Put it in front, because the number less than the reference number should not appear after the reference number
        array[start] = array[end];
        // Find a number greater than the reference number from the left
        while (array[start] <= piv) {
            start ++;
        }
        // Put it behind, because numbers larger than the benchmark should not appear before the benchmark
        array[end] = array[start];
    }
    // The position where the left and right pointers meet is the position where the benchmark number should be after the array is ordered. Because after the previous round of exchange, the left side of the position is all less than the reference number, and the right side is all greater than the reference number
    array[end] = piv;
    // Returns the position where the reference number should be, and the position where the reference number should be after the array is ordered
    return end;
}

Time complexity:

Time complexity	Average: O(n * log(n))	Best (evenly divided): O(n * log(n))	Worst case (ordered): O(n^2)

If it is divided evenly, the recursive logn layer traverses n numbers each time, so the time complexity is O(nlogn). If it is ordered, the reference position does not need to be moved. Each time, the interval will be divided by the first position, which is equivalent to that there is no interval and recursive n layers are required, so the time complexity is O(n^2).

Space complexity:

Time complexity	Average: O(log(n))	Best (evenly divided): O(log(n))	Worst case: O(n)

The reason is the same as above, the same as the number of recursive layers.

Stability: unstable
Optimization: for the purpose of more uniform division of intervals

1. Randomly selected benchmark
2. Three numbers middle method: select three numbers (leftmost, rightmost and middle) and exchange the number of middle size with the first number

Merge sort

7. Merge and sort

Illustration:

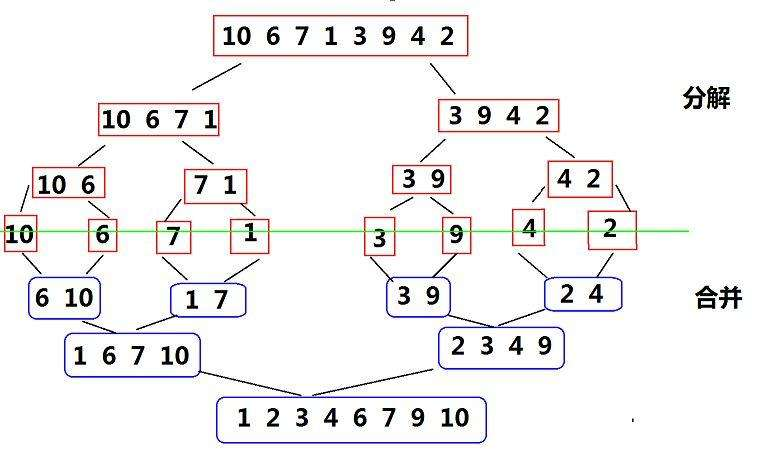
Thought: if the array has only one number, it must be orderly. Merge sort, first decompose the array into the smallest subsequence, and then merge them, transforming the problem into merging two ordered sequences. It's used in the same fast platoon here Divide and conquer idea (put a connection first and talk later).

// 7. Merge and sort
public static void mergeSort(int[] array) {
    mergeSortInternal(array, 0, array.length - 1);
}
// recursion
private static void mergeSortInternal(int[] array, int low, int high) {
    // End condition
    if (low >= high) return;
    int mid = (low + high) / 2;
    // Recursive left and right parts
    mergeSortInternal(array, low, mid);
    mergeSortInternal(array, mid + 1, high);
    // merge
    merge(array, low, mid, high);
}
// Merge two ordered arrays array 1: [low, mid] array 2: [mid+1, high]
private static void merge(int[] array, int low, int mid, int high) {
    // Starting position of two sections
    int s1 = low;
    int s2 = mid + 1;
    // Merge result acceptance array
    int tmp[] = new int[high - low + 1];
    int k = 0;
    // When s1 and s2 are not out of bounds, put the smaller number in front
    while (s1 <= mid && s2 <= high) {
        if (array[s1] <= array[s2]) {
            tmp[k++] = array[s1++];
        }
        if (array[s2] <= array[s1]) {
            tmp[k++] = array[s2++];
        }
    }
    // The rest of the two sections can be added to the back
    while (s1 <= mid) {
        tmp[k++] = array[s1++];
    }
    while (s2 <= high) {
        tmp[k++] = array[s2++];
    }
    // Copy back to the original array
    for (int i = 0; i < tmp.length; i++) {
        // Note that the copy interval starts at low
        array[low + i] = tmp[i];
    }
}

Time complexity: analog fast scheduling, O(n * log(n))
Space complexity: O(n)
Stability: stable

stability

If the sorting algorithm can ensure that the relative position of two equal data does not change after sorting, we call the algorithm a stable sorting algorithm
Law.

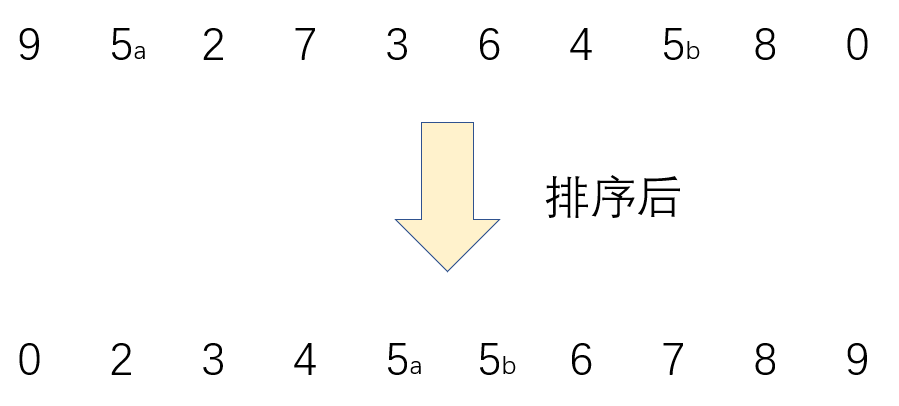
Non recursive implementation of fast sorting and merge sorting

Fast exhaust:

public static void quickSort2(int[] array) {
    Stack<Integer> stack = new Stack<>();
    int low = 0;
    int high = array.length - 1;
    int piv = pivot(array, low, high);
    if (piv > low + 1) {  //Judge that there are at least two elements on the left
        stack.push(low);
        stack.push(piv - 1);
    }
    if (piv < high - 1) {
        stack.push(piv + 1);
        stack.push(high);
    }
    while (!stack.empty()) {
        high = stack.pop();
        low = stack.pop();
        piv = pivot(array, low, high);
        if (piv > low + 1) {
            stack.push(low);
            stack.push(piv - 1);
        }
        if (piv < high - 1) {
            stack.push(piv + 1);
            stack.push(high);
        }
    }
}

Merge sort:

public static void mergeSort1(int[] array) {
    for (int i = 1; i < array.length; i *= 2) {
        merge1(array, i);
    }
}
private static void merge1(int[] array, int gap) {
    int s1 = 0;
    int e1 = s1 + gap - 1;
    int s2 = e1 + 1;
    int e2 = s2 + gap - 1 < array.length ? s2 + gap - 1 : array.length - 1;  // Prevention of cross-border
    int[] tmp = new int[array.length];
    int k = 0;

    while (s2 < array.length) {   // There are two merging segments
        while (s1 <= e1 && s2 <= e2) {
            if (array[s1] <= array[s2]) {
                tmp[k++] = array[s1++];
            }
            if (array[s2] <= array[s1]) {
                tmp[k++] = array[s2++];
            }
        }
        while (s1 <= e1) {
            tmp[k++] = array[s1++];
        }
        while (s2 <= e2) {
            tmp[k++] = array[s2++];
        }
        s1 = e2 + 1;
        e1 = s1 + gap - 1;
        s2 = e1 + 1;
        e2 = s2 + gap - 1 < array.length ? s2 + gap - 1 : array.length - 1;
    }
    while (s1 < array.length) {
        tmp[k++] = array[s1++];
    }
    for (int i = 0; i < tmp.length; i++) {
        array[i] = tmp[i];
    }

}

Test code

public class TestDemo {
    public static void main(String[] args) {
        int[] array = {6,6,4,2,9,5,7,1,3};
        System.out.println(Arrays.toString(array));
        //Sort.insertSort(array);
        //Sort.shellSort(array);
        //Sort.selectSort(array);
        //Sort.heapSort(array);
        //Sort.bubbleSort(array);
        //Sort.quickSort(array);
        //Sort.quickSort1(array);
        //Sort.quickSort2(array);
        Sort.mergeSort(array);
        //Sort.mergeSort1(array);
        System.out.println(Arrays.toString(array));
    }
}