frexp is a function of math module in c language and python. This function does not exist in java. It seems that it is difficult to find relevant descriptions on the Internet.
The function of frexp is to decompose a number into mantissa, base and exponential exponent. Generally, the default base is 10 or 2. More often, the default is 2. For example, the implementation of the function of frexp in c/python.
Here is an example of python.
>>> import math >>> m,e = math.frexp(18) >>> m,e (0.5625, 5) >>> m * 2 ** e 18.0 >>>
The number 18 is finally decomposed into:
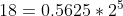
Similarly, in c language, the same results can be obtained:
#include <stdio.h>
#include <math.h>
int main(){
double x = 18,m;
int e;
m = frexp(x,&e);
printf("%.2lf = %.4lf * 2 ^ %d\n",x,m,e);
return 0;
}Screenshot of running code:
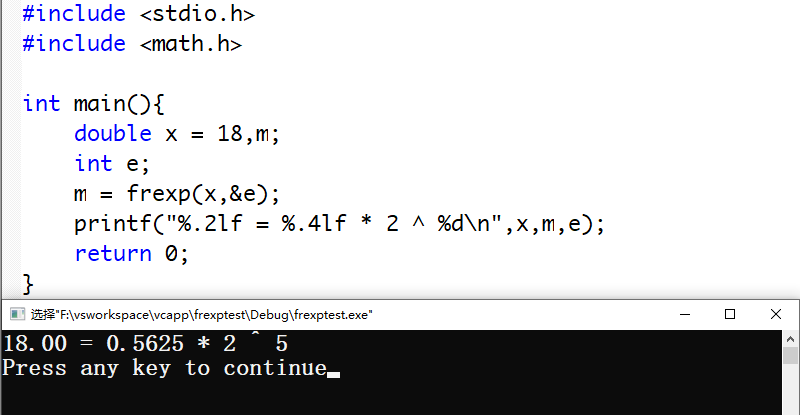
One feature of this decomposition is that mantissa is a number between (0.5,1).
For the implementation in java, you can refer to the following code:
public class FrexpDemo {
public static FRexpResult frexp(double value) {
final FRexpResult result = new FRexpResult();
long bits = Double.doubleToLongBits(value);
double realMant = 1.;
// Test for NaN, infinity, and zero.
if (Double.isNaN(value) || value + value == value || Double.isInfinite(value)) {
result.exponent = 0;
result.mantissa = value;
} else {
boolean neg = (bits < 0);
int exponent = (int) ((bits >> 52) & 0x7ffL);
long mantissa = bits & 0xfffffffffffffL;
if (exponent == 0) {
exponent++;
} else {
mantissa = mantissa | (1L << 52);
}
// bias the exponent - actually biased by 1023.
// we are treating the mantissa as m.0 instead of 0.m
// so subtract another 52.
exponent -= 1075;
realMant = mantissa;
// normalize
while (realMant > 1.0) {
mantissa >>= 1;
realMant /= 2.;
exponent++;
}
if (neg) {
realMant = realMant * -1;
}
result.exponent = exponent;
result.mantissa = realMant;
}
return result;
}
public static void main(String[] args) {
FRexpResult r = frexp(18);
System.out.println(r);
}
}
class FRexpResult {
public int exponent = 0;
public double mantissa = 0.;
@Override
public String toString() {
return String.format("mantissa=%f,exponent=%d", mantissa,exponent);
}
}
After simple verification, we can get similar results with python/c.
===============================================
In addition, there is another implementation method. The code is as follows:
public class Test {
public class FRex {
public FRexPHolder frexp(double value) {
FRexPHolder ret = new FRexPHolder();
ret.exponent = 0;
ret.mantissa = 0;
if (value == 0.0 || value == -0.0) {
return ret;
}
if (Double.isNaN(value)) {
ret.mantissa = Double.NaN;
ret.exponent = -1;
return ret;
}
if (Double.isInfinite(value)) {
ret.mantissa = value;
ret.exponent = -1;
return ret;
}
ret.mantissa = value;
ret.exponent = 0;
int sign = 1;
if (ret.mantissa < 0f) {
sign--;
ret.mantissa = -(ret.mantissa);
}
while (ret.mantissa < 0.5f) {
ret.mantissa *= 2.0f;
ret.exponent -= 1;
}
while (ret.mantissa >= 1.0f) {
ret.mantissa *= 0.5f;
ret.exponent++;
}
ret.mantissa *= sign;
return ret;
}
}
public class FRexPHolder {
int exponent;
double mantissa;
}
public static void main(String args[]) {
new Test();
}
public Test() {
double value = 18.0;
// double value = 0.0;
// double value = -0.0;
// double value = Double.NaN;
// double value = Double.NEGATIVE_INFINITY;
// double value = Double.POSITIVE_INFINITY;
FRex test = new FRex();
FRexPHolder frexp = test.frexp(value);
System.out.println("Mantissa: " + frexp.mantissa);
System.out.println("Exponent: " + frexp.exponent);
System.out.println("Original value was: " + value);
System.out.print(frexp.mantissa + " * 2^" + frexp.exponent + " = ");
System.out.println(frexp.mantissa * (1 << frexp.exponent));
}
}The operation results are similar:

What is the function of this decomposition? In general, it may not be used until I use asn1 to parse real number types and find that both the C language library asn1c and python's asn1tools adopt the method of decomposing data into a mantissa * base(2) ^ exponent when encoding real number types, I found this frexp decomposition useful.
Through the above example, we find that mantissa is a floating-point number between (0.5,1), while asn1 codec enlarges the number to an integer again. For example:
18 = 9 * 2^1 // mantissa = 9 exponent = 1 20 = 5 * 2^2 // mantissa = 5 exponent = 2 19 = 19* 2^0 // mantissa = 19 exponent = 0
To make mantissa an integer, you still need to use the above frexp function.
As shown below, this code is the encoding operation of real numbers in asn1tools tool, which is to decompose real numbers into mantissa * 2^ In the form of exponent, and then only the byte code of mantissa and exponent is stored. The cardinality 2 is directly ignored. Mantissa here is an integer, that is, use frexp to decompose the real number into the form of preliminary mantissa * 2 ^ exponent, and then enlarge mantissa to an integer through various operations.
import math
import binascii
def lowest_set_bit1(value):
offset = (value & -value).bit_length() - 1
if offset < 0:
offset = 0
return offset
def encode_real(data):
if data == float('inf'):
data = b'\x40'
elif data == float('-inf'):
data = b'\x41'
elif math.isnan(data):
data = b'\x42'
elif data == 0.0:
data = b''
else:
if data >= 0:
negative_bit = 0
else:
negative_bit = 0x40
data *= -1
mantissa, exponent = math.frexp(abs(data))
mantissa = int(mantissa * 2 ** 53)
lowest_set_bit = lowest_set_bit1(mantissa)
mantissa >>= lowest_set_bit
mantissa |= (0x80 << (8 * ((mantissa.bit_length() // 8) + 1)))
mantissa = binascii.unhexlify(hex(mantissa)[4:].rstrip('L'))
exponent = (52 - lowest_set_bit - exponent)
if -129 < exponent < 128:
exponent = [0x80 | negative_bit, ((0xff - exponent) & 0xff)]
elif -32769 < exponent < 32768:
exponent = ((0xffff - exponent) & 0xffff)
exponent = [0x81 | negative_bit, (exponent >> 8), exponent & 0xff]
else:
raise NotImplementedError(
'REAL exponent {} out of range.'.format(exponent))
data = bytearray(exponent) + mantissa
return dataThis code can also be implemented in java, but it is much more complex. Many data types need to be redefined and cannot be reused directly like python.