1, Principle of cued binary tree
Introduced earlier Binary tree The article mentioned that the binary tree can use two storage structures: sequential storage and chain storage. When using chain storage, there will be a large number of empty finger needle fields. In order to make full use of these empty finger needle fields, a cued binary tree is extended to use these empty finger needle fields and improve the retrieval efficiency.
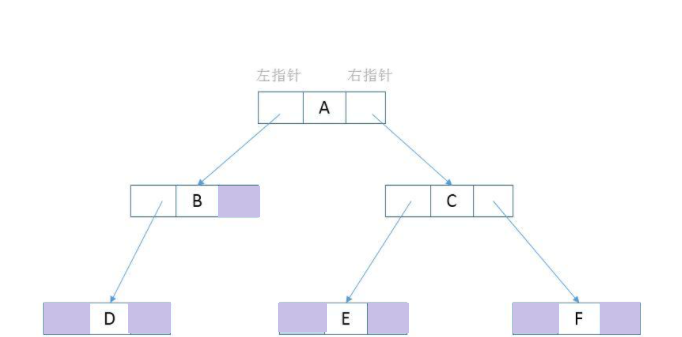
In the figure above, the purple area is the empty finger fields that are not pointed to. From the perspective of storage space, these empty finger fields waste memory resources.
From another perspective, if you need to know the predecessor and successor nodes of node C, you need to traverse each time. Can you store the predecessor and successor nodes of node C in advance, so as to save the traversal operation and improve efficiency?
Based on the above analysis, we can make full use of the null pointer field in the binary list to store the pointers of the precursor and successor nodes of the node in a certain traversal mode.
This pointer to the precursor and successor becomes the clue, and the binary chain of the clue becomes the clue list, and the corresponding binary tree is called Threaded Binary Tree
2, Constructing threaded binary tree
- First, the binary tree shall be traversed in medium order (for those who do not understand the traversal of binary tree, please refer to the data structure: binary tree), and the pointer field with empty right pointer of all nodes shall be pointed to its subsequent nodes, as shown in the following figure:
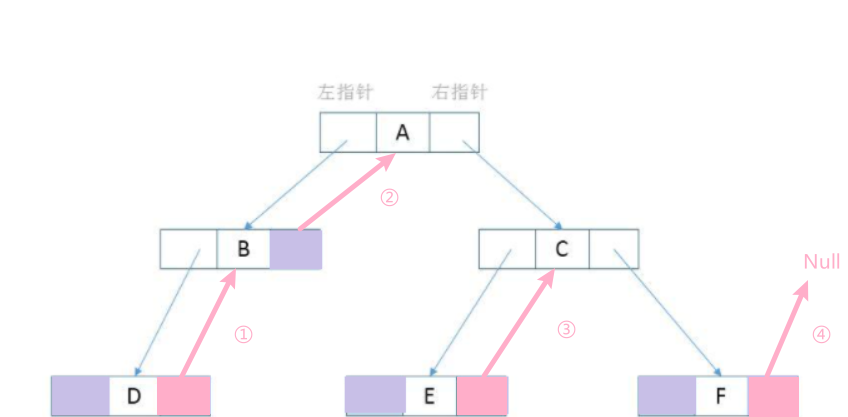
By traversing node D in the middle order, it is found that the right pointer of node D is Null, and the successor node of node D is B, so the right node of D points to node B (as shown in operation ① in the above figure), and the right pointer of node B is Null, so the right pointer points to node A (as shown in operation ② in the above figure), and so on. If the successor node to node f is Null, the right pointer of F points to Null.
-
Next, point all pointers with null left pointer to its precursor node, as shown in the following figure:
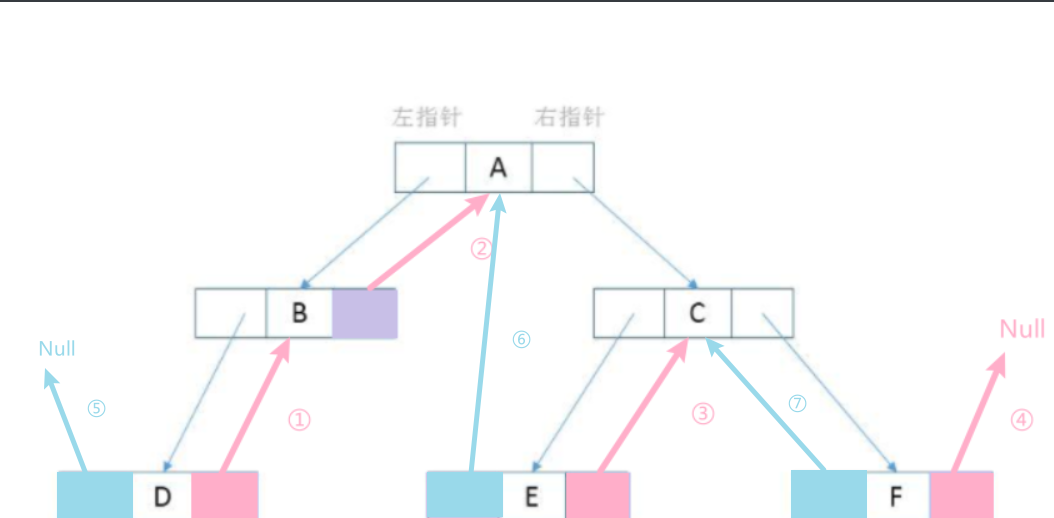
As shown in the figure above, the left pointer field of node D points to Null (operation ⑤), the precursor node of node E is A, the left pointer of node E points to node A, and so on, and the left node of node F points to node C.
-
Through the above two steps, the clue of the whole binary tree is completed.
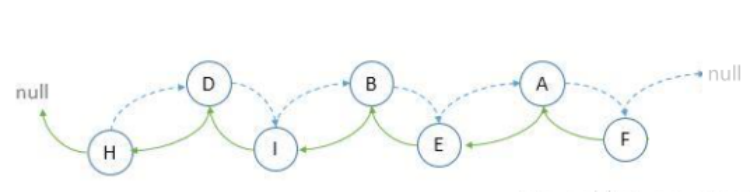
After cueing, it can be seen (the blue arrow indicates the precursor and the pink arrow indicates the successor) that the cued binary tree is equivalent. Therefore, the binary tree is converted into a special two-way linked list, which brings convenience to add, delete and find nodes and improves efficiency. The diagram after converting to a linked list is as follows:
Cue needs to modify the structure of the node. The modified data structure is as follows:
class Node
{
private int num;
private Object data; //Data domain
private Node left; //Left pointer field
private Node right; //Right pointer field
/**
* leftType == 0 Indicates that it points to the left subtree. If it is 1, it points to the precursor node
*/
private int leftType;
/**
* rightType == 0 Indicates that it points to the right subtree. If it is 1, it points to the successor node
*/
private int rightType;
}
3, Code implementation clue binary tree
-
Node structure
class Node { private int num; private Object data; private Node left; private Node right; /** * leftType == 0 Indicates that it points to the left subtree. If it is 1, it points to the precursor node */ private int leftType; /** * rightType == 0 Indicates that it points to the right subtree. If it is 1, it points to the successor node */ private int rightType; public Node(int num, Object data) { this.num = num; this.data = data; } /** * Preorder traversal */ public void preOrder() { //Output parent node information first System.out.println(this); //Judge whether the left node of this node is empty //If the left node is not null and the pointer type is not a precursor type if (this.left != null && this.leftType != 1) { //Left preorder traversal this.left.preOrder(); } //Judge whether the right node of this node is empty //If the right node is not null and the pointer type is not a successor type if (this.right != null && this.rightType != 1) { //Forward right traversal this.right.preOrder(); } } /** * Middle order traversal cued binary tree */ public void infixOrder() { //Judge whether the left node of this node is empty if (this.left != null && this.leftType != 1) { //Left middle order traversal this.left.infixOrder(); } //Output parent node information System.out.println(this); //Judge whether the right node of this node is empty if (this.right != null && this.rightType != 1) { //Right middle order traversal this.right.infixOrder(); } } /** * Postorder traversal */ public void postOrder() { //Judge whether the left node of this node is empty if (this.left != null && this.leftType != 1) { //Left postorder traversal this.left.postOrder(); } //Judge whether the right node of this node is empty if (this.right != null && this.rightType != 1) { //Right backward traversal this.right.postOrder(); } //Output parent node information System.out.println(this); } //get set method omitted @Override public String toString() { return "Node{" + "num=" + num + ", data=" + data + '}'; } } -
Threaded binary tree structure
/** * Define ThreadedBinaryTree to realize the binary tree of cueing function */ class ThreadedBinaryTree { /** * Root node */ private Node root; /** * To achieve cueing, you need to create a pointer to the predecessor node of the current node * When cueing recursively, pre always keeps the previous node */ private Node pre = null; public void setRoot(Node root) { this.root = root; } public void createBinaryTree(ArrayList<Node> list) { this.createBinaryTree(list,0); } /** * Create binary tree * @param list Node list * @param index Index for creating * @return */ private Node createBinaryTree(ArrayList<Node> list, int index) { Node node = null; if (isEmpty()) { setRoot(list.get(0)); } if (index < list.size()) { node = list.get(index); node.setLeft(createBinaryTree(list, (2*index+1))); node.setRight(createBinaryTree(list, (2*index+2))); } return node; } public boolean isEmpty() { return root == null; } public void preThreadNodes() { this.preThreadNodes(root); } public void infixThreadNodes() { this.infixThreadNodes(root); } public void postThreadNodes() { this.postThreadNodes(root); } /** * Preordered cued binary tree * @param node Current nodes requiring cueing */ private void preThreadNodes(Node node) { //Recursive backtracking condition if (node == null) { return; } //Traverse to leaf node (the precursor pointer is not used) if (node.getLeft() == null) { node.setLeft(pre); node.setLeftType(1); } //pre.getLeft() != node must be indispensable //Otherwise, after the first backtracking to the parent node, if this judgment is not added, the post drive pointer of the pre node will point to the parent node //At this time, the predecessor and successor nodes of pre point to the parent node, which will inevitably lead to a life and death cycle and cannot end the recursion if (pre != null && pre.getRight() == null && pre.getLeft() != node) { pre.setRight(node); pre.setRightType(1); } pre = node; if (node.getLeftType() == 0) { preThreadNodes(node.getLeft()); } preThreadNodes(node.getRight()); } /** * Medium order cued binary tree * @param node Current nodes requiring cueing */ private void infixThreadNodes(Node node) { if (node == null) { return; } //1. Recursive cued left subtree infixThreadNodes(node.getLeft()); //2. Cue the current node //Process the precursor node of the current node if (node.getLeft() == null) { //Make the left pointer of the current node point to the predecessor node node.setLeft(pre); //Modify the type of the left pointer of the current node node.setLeftType(1); } //Processing successor nodes if (pre != null && pre.getRight() == null) { //Let the right pointer of the predecessor node point to the current node pre.setRight(node); //Modify the right pointer type of the precursor node pre.setRightType(1); } //After each node is processed, make the current node the precursor of the next node pre = node; //3. Recursive cued right subtree infixThreadNodes(node.getRight()); } /** * Post ordered cued binary tree * @param node Current nodes requiring cueing */ private void postThreadNodes(Node node) { if (node == null) { return; } postThreadNodes(node.getLeft()); postThreadNodes(node.getRight()); if (node.getLeft() == null) { node.setLeft(pre); node.setLeftType(1); } if ( pre!= null && pre.getRight() == null ) { pre.setRight(node); pre.setRightType(1); } pre = node; } /** * A method of traversing cued binary tree in order in non recursive way */ public void threadedInfixList() { Node node = root; while (node != null) { //Loop to find node with leftType == 1 while (node.getLeftType() == 0) { node = node.getLeft(); } System.out.println(node); while (node.getRightType() == 1) { node = node.getRight(); System.out.println(node); } node = node.getRight(); } } public void threadedTreePreList() { if (root != null) { root.preOrder(); }else { System.out.println("Binary tree is empty,Unable to traverse"); } } public void threadedTreeInfixList() { if (root != null) { root.infixOrder(); }else { System.out.println("Binary tree is empty,Unable to traverse"); } } public void threadedTreePostList() { if (root != null) { root.postOrder(); }else { System.out.println("Binary tree is empty,Unable to traverse"); } } }
above.
If there are deficiencies or errors, please comment and correct.
It's not easy to tidy up. Leave it for three times before you go!