introduction

It's an interpolation search algorithm. I think it's better to call it a difference search algorithm. Because the search range is determined according to the difference of relevant data. In the follow-up of this paper, I will replace the interpolation search algorithm with the difference search algorithm.

What is difference finding algorithm

Ask about the difference search algorithm, then you should already know what is the binary search algorithm.

What? You don't know yet? Click here to learn about the binary search algorithm)

To put it simply, the difference search algorithm is a small optimization of the binary search algorithm.

Optimize content

The formula for taking the midpoint value is different.
In the binary search algorithm, we take the formula of mid as follows

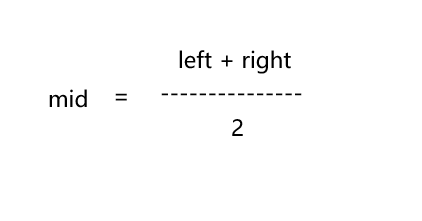
For subsequent derivation, let's change it

However, in the difference search algorithm, we take the formula of mid as follows:

This is the difference between the two algorithms. Therefore, to understand interpolation sorting, you only need to understand this formula. Next, let's analyze this formula.

Difference search idea

Before explaining this formula, we need to know what the idea of difference search is.
The idea of binary search is to divide it into half directly, and then process half each time. However, if the value we find is on the far left or right, we must divide it to the end one at a time.

Is it possible that I can reduce the search range to 1 / 3, 1 / 4 or less of the last array? This is what the difference search algorithm needs to do to reduce the search range.

Formula analysis

So how is it implemented? Let's look at two formulas for taking mid

The difference lies in the first parameter. The binary search value is 1 / 2
And the difference search is

Let's look at the meaning of these variables:
Target: find the target value
arr[left]: you need to find the value of the left element of the array
arr[right]: you need to find the value of the right element of the array

Therefore, when the value of the above formula is less than 1 / 2, the obtained mid is smaller, and the midpoint is closer to the left at the left end.

So if the target value is right to the left of mid, do we narrow the next search range?

Please pay attention to the above paragraph

Let's pay attention to the following situation: when the array is evenly distributed (such as 0, 2, 4, 6, 8, 16...), how many times does the difference search algorithm need to be found? Let's see the following formula derivation

Suppose the leftmost value is L
There are n elements in the array
The difference between two adjacent numbers is k
The subscript of the desired target is i
Then target = L + i*k,
arr[ right ] - arr[ left ] = (n - 1) * k ,
right - left = n - 1.
If you put it into the above formula, it becomes

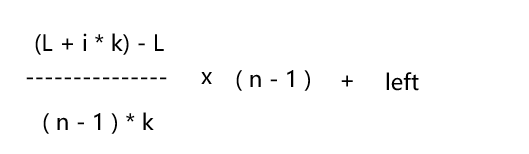
After the reduction transformation, you get

Because the starting position of binary search starts from 0, getting mid = i in the first search is to directly find the subscript of the value to be searched.

Therefore, when the array is evenly distributed, the difference search only needs to find the desired result once.

Limitations of difference search algorithm

After reading the above derivation, do you think the difference sorting is very powerful. But remember the sentence I asked you to pay attention to?

Although we can narrow the range of one side, we can't guarantee that the data we are looking for is on that side. That is, I divide the array according to mid: the left side accounts for 1 / 3 of the original array and the right side accounts for 2 / 3, but the data I need to find is on the right. At this time, when I need to find the range, 2 / 3 is larger than 1 / 2 of binary search, and I need to find more data.

For example, in such an array [0, 1, 5, 7, 8, 12, 100], our target = 8. According to the above formula

The obtained mid is 0.48, rounded down to 0, and the next search range is [1, 6]
It is larger than the range [4,6] obtained by binary search.

In the above case, the difference search algorithm can only search from beginning to end, and degenerates into a sequential search algorithm.

Therefore, the difference sorting is not very stable, but if it can be determined that the array is evenly distributed or the difference between adjacent values is not very large, the difference search algorithm is better than the binary search algorithm.

code implementation

public class Test {
	/*
	 * Interpolation lookup
	 */
	public static int interpolationSearch(int[] arr, int target , int left , int right) {
		if(target < arr[left] || target > arr[right] || left > right){
			return -1;				
		}

		int leftToTarget = target - arr[left];
		int rightToLeft = arr[right] - arr[left];
		int num = right - left;
		//The subscript of the middle value. Note the difference between this line and binary search
		int mid = left + leftToTarget*num/rightToLeft;
		System.out.println("Found once, the middle value is:" + mid);
		//If the target value is less than the middle value, take the left
		if(arr[mid] > target && left <= right) {
			//Recursive left
			return interpolationSearch(arr,target , left , mid-1);
		}else if(arr[mid] < target && left <= right) {
			//The target value is greater than the middle value, take the right and recurse
			return interpolationSearch(arr,target, mid+1 , right);
		}else {
			//Not greater than or less than is equal
			return mid;
		}
	}

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		System.out.println("======== Difference lookup array with slightly uneven distribution ===========");
		int arr[] = {1 ,4, 9, 15, 27, 49, 128, 157};
		int result = interpolationSearch(arr, 9, 0, arr.length - 1);
		System.out.println(result==-1?"Element not found!":"Search succeeded!" + 9 + "Corresponding subscript: " + result);
		
		System.out.println("======== Difference lookup evenly distributed array ===========");
		int arr1[] = {0, 2, 4, 6, 8, 10, 12, 14, 16, 18 ,20};
		int target = 8;
		int result1 = interpolationSearch(arr1, target, 0, arr1.length - 1);
		System.out.println(result1==-1?"Element not found!":"Search succeeded!" + target + "Corresponding subscript: " + result1);
		
		System.out.println("======== Difference lookup array with extremely uneven distribution ===========");
		int arr2[] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,99999};
		int target2 = 8;
		int result2 = interpolationSearch(arr2, target2, 0, arr2.length - 1);
		System.out.println(result2==-1?"Element not found!":"Search succeeded!" + target2 + "Corresponding subscript: " + result2);
		
		
	}

}