Method overloading

1. Method overloading is also known as: overload
 2. When to consider using method overloading?
When the functions are similar, try to keep the method names the same.
[but: when the functions are different / different, try to make the method names different. ]
3. What conditions are met to form a method overload?
★ in the same category
	Same method name
	The parameter list is different: 
	Different quantity
	Different order
	Different types
 4. What does method overloading have to do with, and nothing to do with? 
Method overload is related to method name + parameter list
 Method overload is independent of return value type
 Method overloading is independent of modifier list

Code example:

public class overload {

	public static void main(String[] args) {
		overload.m1();
		overload.m1(20);
		overload.m2(5.11, 9.99);
		overload.m2(50, 20);

	}
	public static void m1() {
		System.out.println("This is void m1 Medium print output");
	}
	public static void m1(int a) {
		System.out.println("This is int type m1 Output in a"+a);
	}
	
	public static void m2(int a,int b) {
		System.out.println("int int Type I output a"+a+"b:"+b);
	}
	public static void m2(double a,double b) {
		System.out.println("double double Type output a:"+a+"b:+b");
	}
}

Recursive call

On recursive calling of methods
1. What is recursion?
Method calls itself.
Call yourself directly or indirectly.
a() {
a();
}
2. Recursion consumes a lot of stack memory. Do not use recursion algorithm when it is not used.
3. The following program ran with an Error [not an exception, but an Error error]:
Stack memory overflow error,
The error can't be retrieved, only one result is that the JVM stops working.
4. Recursion must have an end condition. If there is no end condition, a stack memory overflow error will occur.
5. Even if there is an end condition for recursion, even if the end condition is correct, stack memory overflow error may occur.
Because recursion calls too much when it does some algorithms. .
Be careful:
Recursion can be used sparingly
But in some cases, the implementation of this function must rely on recursion, such as depth first search and breadth first search.

Example: sum 1~N recursively:
The code is as follows:

public class recursion {

	public static void main(String[] args) {
		int n=100;
		int retValue= sum(n);
		System.out.println(retValue);
	}
	public static int sum(int n) {
		if(n==0) return 0;
		else return sum(n-1)+n;
	}
}

Example 2: calculating the factorial of N
The code is as follows:

public class recursion {

	public static void main(String[] args) {
		int n=5;
		int retValue= sum(n);
		System.out.println(retValue);
	}
	public static int sum(int n) {
		if(n==1) return 1;
		else return sum(n-1)*n;
	}
}

Concept diagram of recursive calling process: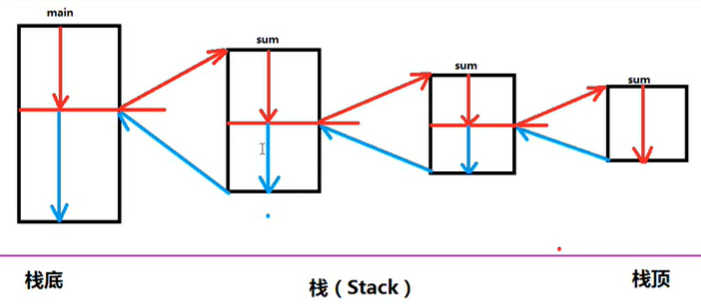

Example 3: Calculation of fiboracci series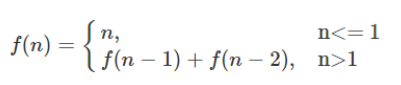

The code is as follows:

public class recursion {
	//1 1 2 3 5 8 13 21 34 55 89 144
	public static void main(String[] args) {
		int n=12;
		int retValue= sum(n);
		System.out.println(retValue);
	}
	public static int sum(int n) {
		if(n==1 || n==2) return 1;
		else return sum(n-1)+sum(n-2);
	}
}

Example 4: Hanoi Tower problem
The mathematical description is:
There are three rods x, Y, Z. There are N (N > 1) perforated disks on the X-bar, and the size of the disks decreases from bottom to top. It is required to move all discs to the Y-bar according to the following rules:

1. Only one disc can be moved at a time;
2. The large plate cannot be stacked on the small plate.
   Recursive thinking:
3. Move the n-1 disks on the X-bar to the free Z-Bar, and all the above conditions are met
4. Move the nth disc on the X-bar to Y
5. The rest of the problem is to move n-1 disks on the Z-Bar to Y
   The formula description is a bit troublesome. Let's describe it in words:
6. With the Y-bar as the intermediary, move the first n-1 disc from the X-bar to the Z-Bar (itself is an n-1 Hanoi Tower problem! )
7. Move the n th disc to the Y-bar
8. With the X-bar as the intermediary, move the N-1 disk on the Z-Bar to the Y-bar (itself is an n-1 Hanoi Tower problem! )

package helloworld;

public class recursion {
	 //1 1 2 3 5 8 13 21 34 55 89 144
	static int num=0;
	public static void main(String[] args) {
		int n=12;
		recursion.hanoi(10, 'x', 'z', 'y');
		System.out.println(num);
	}
	public static void hanoi(int n,char from,char tmp,char to) {
		if (n>0) {
			 num++;
	         hanoi(n - 1, from, to, tmp);
	         System.out.println("take " + n + " from " + from + " to " + to);
	         num++;
	         hanoi(n - 1, tmp, from, to);
	    }
	}
	
}