Video link: https://www.bilibili.com/video/BV1Rx411876f?p=1

Video range P576 - P583

1. Bubble sorting algorithm

1. After each cycle, find the largest data and put it on the far right of the pile of data involved in the comparison. (the biggest bubble)
2. Core: compare the number on the left with the number on the right. When the left > right, change the position

package array;

public class BubbleSort {

    public static void main(String[] args) {

        //Static initialization array
        int[] array = {10,5,65,54,1,2,9};

        //Define the counter and record the total number of comparisons
        int count = 0;

        //Bubble sort algorithm 
        for (int i = array.length - 1; i > 0 ; i--) {
            for (int j = 0; j < i; j++) {

                //Do not need to exchange positions, be sure to compare them once
                count++;

                //change of position
                if (array[j] > array[j + 1]){
                    int temp;
                    temp = array[j];
                    array[j] = array[j + 1];
                    array[j + 1] = temp;
                }
            }
        }

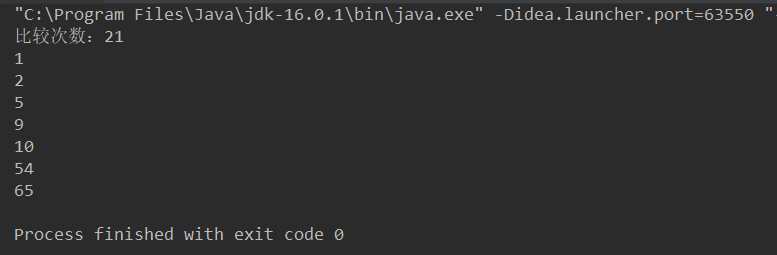
        System.out.println("Number of comparisons:" + count);

        for (int i = 0; i < array.length; i++) {
            System.out.println(array[i]);
        }
    }
}

Operation results:

2. Select Sorting Algorithm

1. Each time, find the minimum value from the pile of "data participating in the comparison", and exchange the position with the "top element of the pile participating in the comparison"
2. Selective sorting is better than bubble sorting: every exchange of positions is meaningful
3. The number of comparisons between bubble sorting and selective sorting has not changed, but the number of exchanges between selective sorting has decreased

Algorithms in video:

package array;

public class SelectSort {
    public static void main(String[] args) {
        int[]  array = {4,5,9,2,45,62,1,6,8,7,12};

        int count = 0;

        //Select Sorting Algorithm
        for (int i = 0; i < array.length - 1; i++) {

            int min = i;

            for (int j = i + 1; j < array.length; j++) {
                count++;
                if (array[j] < array[min]){
                    min = j;//Minimum element subscript j
                }
            }

            if (min != i){
                int temp;
                temp = array[min];
                array[min] = array[i];
                array[i] = temp;
            }
        }

        System.out.println("Number of comparisons:" + count);

        for (int i = 0; i < array.length; i++) {
            System.out.println(array[i]);
        }
    }
}

Self written algorithm:

package array;

public class SelectSort {
    public static void main(String[] args) {
        int[]  array = {4,5,9,2,45,62,1,6,8,7,12};


        int count = 0;

        for (int i = 0; i < array.length - 1; i++) {
            int idex = i;
            int min = array[i];

            for (int j = i; j < array.length - 1; j++) {
                count++;
                if (array[j + 1] <= min){
                    idex = j + 1;
                    min = array[idex];
                }
            }

            if (idex == i){
               continue;
            }else{
                int temp;
                temp = array[idex];
                array[idex] = array[i];
                array[i] = temp;
            }

        }
        System.out.println("Number of comparisons:" + count);

        for (int i = 0; i < array.length; i++) {
            System.out.println(array[i]);
        }
    }
}

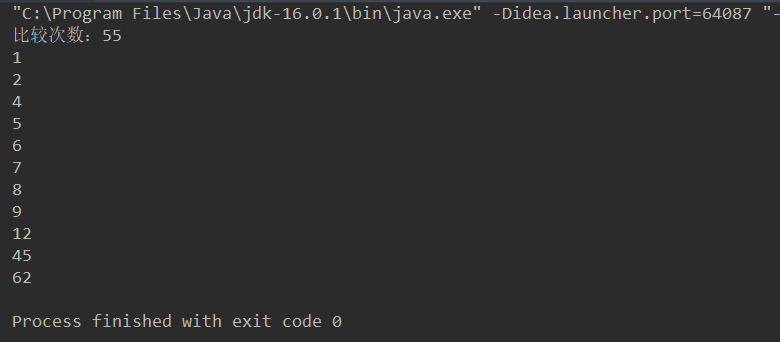
Operation results:

3. Binary (half) search algorithm

There are two ways to find elements of an array:

1. The first kind: look for one by one until you find it
2. The second kind: dichotomy search (algorithm), which is more efficient

3.1 do not use dichotomy

package array;

public class ArraySearch {
    public static void main(String[] args) {

        int[]  array = {4,5,9,2,45,62,1,6,8,7,12};

        int index = arraySearch(array,45);

        System.out.println(index == -1?"The element does not exist!" : "The subscript of this element is:" + index);
    }

    /**
     * Retrieves the index of an element from the array (returns the index of the first element)
     * @param array Retrieved array
     * @param num Retrieved element
     * @return A number greater than or equal to 0 indicates the subscript of the element, - 1 indicates that the element does not exist
     */
    private static int arraySearch(int[] array, int num) {
        for (int i = 0; i < array.length; i++) {
            if (num == array[i]){
                return i;
            }
        }
        return -1;
    }
}

Operation results:

3.2 dichotomy search

1. Dichotomy algorithm is based on sorting (data without sorting cannot be found)
2. The efficiency of binary search is higher than that of "one by one"
3. The termination condition of dichotomy search: keep halving until the element in the middle happens to be the element to be searched
4. The binarySearch function already exists in the code base
   import static java.util.Arrays.binarySearch;

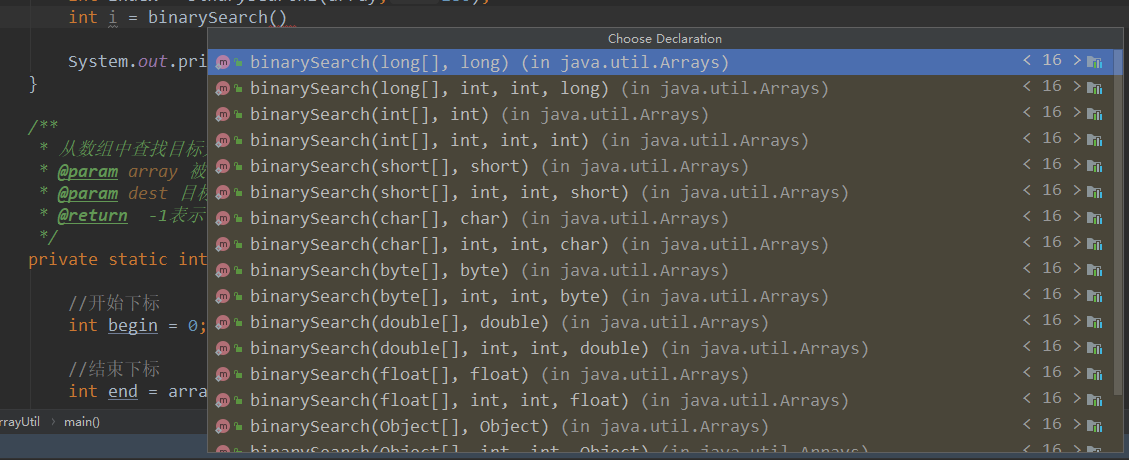
Code example:

package array;

public class ArrayUtil {

    public static void main(String[] args) {
        int[]  array = {1,5,45,63,88,120,180,320};

        int index = binarySearch1(array,180);

        System.out.println(index == -1?"The element does not exist!" : "The subscript of this element is:" + index);
    }

    /**
     * Finds the index of the target element from the array
     * @param array The array to be searched (this must be sorted)
     * @param dest Target element
     * @return  -1 Indicates that the element does not exist, and other indicates that the subscript of the element is returned
     */
    private static int binarySearch1(int[] array, int dest) {

        //Start subscript
        int begin = 0;

        //End subscript
        int end = array.length - 1;

        //As long as the subscript of the start element is to the left of the subscript of the end element, there is a chance to continue the cycle
        while (begin <= end){

            //Intermediate element subscript
            int mid = (begin + end) / 2;

            if (array[mid] == dest){
                return mid;
            }else if (array[mid] < dest){
                //The target is on the right in the middle
                begin = mid + 1;
            }else {
                //The target is on the left in the middle
                end = mid - 1;
            }
        }
        return -1;
    }
}

Operation results:

4. Use of arrays tools

1. SUN company has written an array tool class java for programmers util. Arrays；
2. Refer to the API help document when developing
3. All methods are static

package array;

import java.util.Arrays;

public class ArraysTest02 {

    public static void main(String[] args) {
        int[] array = {1,5,3,6,2,8,9,45,18,16,21};

        //sort
        Arrays.sort(array);

        //output
        for (int i = 0; i < array.length; i++) {
            System.out.println(array[i]);  //Output: 1 2 3 5 6 8 9 16 18 21 45
        }

        //Binary search
        int index = Arrays.binarySearch(array,45);

        //output
        System.out.println(index == -1?"The element does not exist!" : "The subscript of this element is:" + index);//The subscript of this element is: 10
    }
}