Learning objectives of this lecture

1. Understand the principles of structured programming
2. Procedures for mastering sequential structure
3. Master the use of single branch structure

1, Structured programming

(1) Basic principles of structure

1. Top down

• When designing the program, we should first consider the overall situation and then consider the details; First consider the global objectives, and then consider the local objectives. Don't pursue too many details at the beginning. Start the design from the top-level overall goal and gradually concretize the problem.

2. Gradual refinement

• For complex problems, some sub objectives should be designed as a transition and gradually refined.

3. Modularization

• A complex problem must be composed of several simpler problems. Modularization is to decompose the general goal to be solved by the program into sub goals, and then further decompose them into specific small goals. Each small goal is called a module.

4. Restrict goto statements

• It is more flexible to use goto statement when the program is relatively simple, but it is easy to cause confusion in the program flow when the program is relatively complex. It is difficult for others to understand the goto statement later. The process of debugging programs can also become very difficult.

(2) Three process control structures

1. Sequence Structure

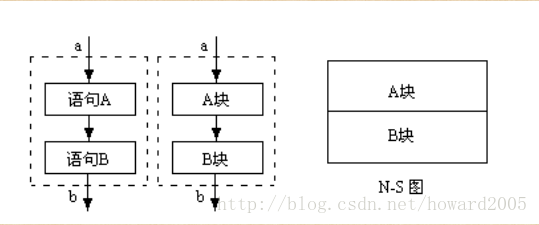
2. Selection Structure

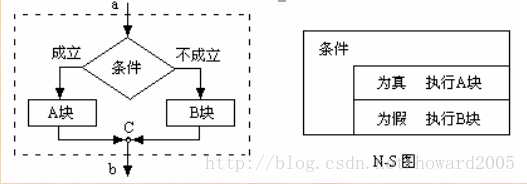
3. Loop Structure

• There are two cases of circular structure
  (1) Pre test condition cycle: check the ticket before boarding (it is possible that one cycle operation will not be executed)
  (2) Post test condition cycle: get on the train before check-in (at least one cycle operation shall be performed anyway)

2, Sequential structure

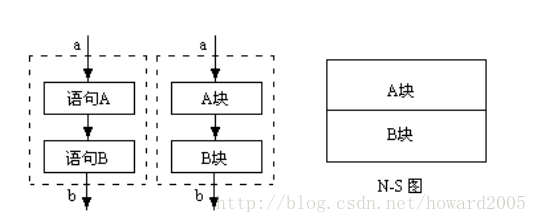
• There is an entry and an exit, and the statements are executed from top to bottom.

(1) Sequence structure diagram

(2) Case demonstration of sequential structure

Case 1: calculate triangle area

package net.hw.lesson06;

import java.util.Scanner;

/**
 * Function: calculate triangle area
 * Author: Wei Hua
 * Date: April 12, 2020
 */
public class Example601 {
    public static void main(String[] args) {
        // Declaration part
        double a, b, c, p, s;
        Scanner sc = new Scanner(System.in);

        // Input part
        System.out.print("a = ");
        a = sc.nextDouble();
        System.out.print("b = ");
        b = sc.nextDouble();
        System.out.print("c = ");
        c = sc.nextDouble();

        // processing section 
        p = (a + b + c) / 2;
        s = Math.sqrt(p * (p - a) * (p - b) * (p - c));

        // Output part
        System.out.println("s = " + s);
    }
}

Run the program to view the results:

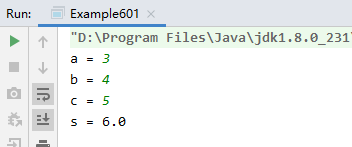
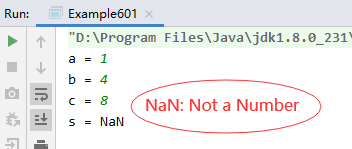
However, if the input a, b and c do not form a triangle, the results are as follows:

Case 2: solving quadratic equation of one variable

package net.hw.lesson06;

import java.util.Scanner;

/**
 * Function: solve quadratic equation of one variable
 * Author: Wei Hua
 * Date: April 12, 2020
 */
public class Example602 {
    public static void main(String[] args) {
        // Declaration part
        double a, b, c, delta, x1, x2;
        Scanner sc = new Scanner(System.in);

        // Input part
        System.out.print("a = ");
        a = sc.nextDouble();
        System.out.print("b = ");
        b = sc.nextDouble();
        System.out.print("c = ");
        c = sc.nextDouble();

        // processing section 
        delta = b * b - 4 * a * c;
        x1 = (-b + Math.sqrt(delta)) / (2 * a);
        x2 = (-b - Math.sqrt(delta)) / (2 * a);

        // Output part
        System.out.println("x1 = " + x1);
        System.out.println("x2 = " + x2);
    }
}

Run the program to view the results:


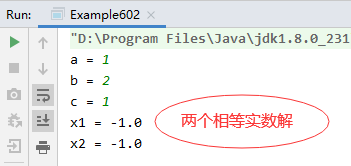
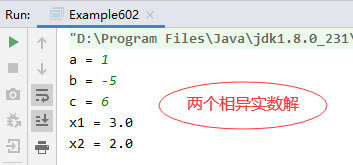
However, the input of a, b and c causes the discriminant to be less than zero and the calculation result cannot be obtained.

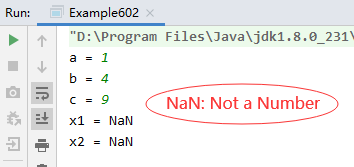
Although the program does not throw exceptions, NaN is not what we want to see.

(3) Summary of sequential structure

• The sequence structure is very simple. It is executed from top to bottom according to the writing order of sentences. In the above two cases, we can see that when we encounter a situation that cannot be solved, we give a NaN result, which is not the result we want. We need to judge whether it can be solved in advance. If it can be solved, we will calculate and give the result; If it cannot be solved, we will give corresponding prompts to tell the user that it cannot be solved. In this way, it is more user-friendly. How to perform different operations according to different situations? This is the selection structure we will talk about next.

3, Selection structure overview

• In real life, we often need to make some judgments. For example, when driving to an intersection, we need to judge the traffic lights. If there is a red light in front, stop and wait, and if it is a green light, pass. There is a special statement in Java called selection structure statement. It also needs to judge some conditions to decide which piece of code to execute.
  
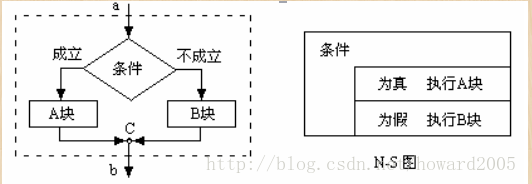
• When the program branches, select whether to execute block a or block B according to whether the conditions in the judgment box are met. No matter whether the conditions are met or not, you can only choose to execute one or one of B. you can't execute block B after executing a block. No matter which path you take, you must pass through point C and then leave this selection structure box.
• According to the number of different cases to be handled, we will explain the following into single branch structure, double branch structure and multi branch structure.

4, Single branch structure

(1) Syntax format

if (condition) {
   Statement group 
}

• Note: if the statement group is only one statement, the curly braces can be omitted.

(2) Implementation

• If the condition holds, execute the statement group, otherwise do nothing.

(3) Case demonstration

Task 1: judge whether a number is even

package net.hw.lesson06;

import java.util.Scanner;

/**
 * Function: judge odd and even numbers
 * Author: Wei Hua
 * Date: April 12, 2020
 */
public class Example603 {
    public static void main(String[] args) {
        // Declaration part
        int n;
        Scanner sc = new Scanner(System.in);

        // Input part
        System.out.print("n = ");
        n = sc.nextInt();

        // Processing part + output part
        if (n % 2 == 0) {
            System.out.println(n + "Is an even number.");
        }
    }
}

Run the program to view the results:


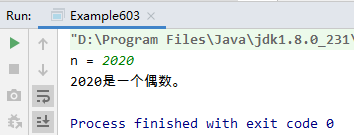
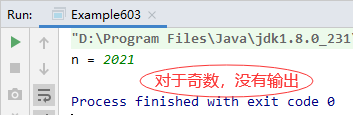
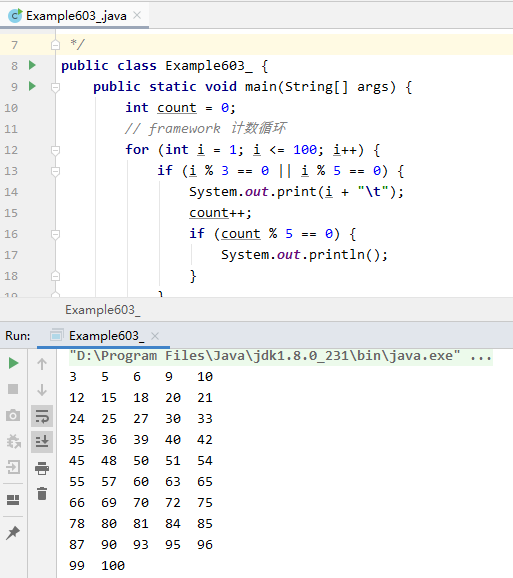
The single branch structure is often nested in the loop structure, which plays a role of filtering. For example, it is necessary to process the numbers that meet the conditions in a certain range.

Task 2. Filter the number of qualified within a certain range

• Output the number between 1 and 100 that can be divided by 3 or 5. It is required to output 5 numbers per line.