Overview and characteristics of arrays

Definition of arrays

An array is an ordered collection of data of the same type. Arrays describe a number of data of the same type, arranged and combined in a certain order. Each data is called an element, and each element can be accessed by an index (subscript). Three basic characteristics of arrays:

1. The length is fixed. Once an array is created, its size is immutable.
2. Its elements must be of the same type and no mixed type is allowed.
3. The array type can be any data type, including the reference type of the basic type.

Old bird advice

Array variables belong to the reference type. Arrays can also be regarded as objects. Each element in an array is equivalent to a member variable with an object. Arrays are objects themselves, and objects in Java are in the heap, so array objects themselves are stored in the heap, regardless of whether they hold the original type or other object types.

7.2.1 Array Declaration

[Example 7-1] Arrays are declared in two ways (for example, one-dimensional arrays)

type[]   arr_name; //(This is recommended)
type    arr_name[];

Matters needing attention

1. The JVM allocates space only when the array object is instantiated, which is related to the length.
2. When declaring an array, no array is actually created.
3. To construct an array, you must specify the length.

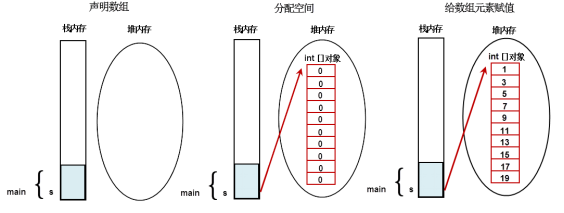
[Example 7-2] Create one-dimensional arrays of basic types

public class Test {
    public static void main(String args[]) {
        int[] s = null; // Declare arrays;
        s = new int[10]; // Allocate space for arrays;
        for (int i = 0; i < 10; i++) {
            s[i] = 2 * i + 1;//Assign values to array elements;
            System.out.println(s[i]);
        } 
    }
}

[Example 7-3] Create a one-dimensional array of reference types

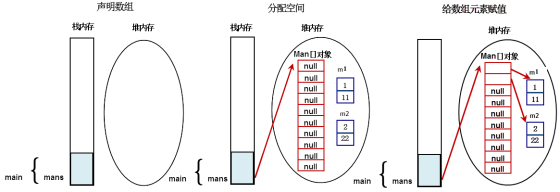
class Man{
    private int age;
    private int id;
    public Man(int id,int age) {
        super();
        this.age = age;
        this.id = id;
    }
}
public class AppMain {
    public static void main(String[] args) {
        Man[] mans;  //Declare an array of reference types; 
        mans = new Man[10];  //Allocate space to the reference type array;
         
        Man m1 = new Man(1,11);
        Man m2 = new Man(2,22);  
         
        mans[0]=m1;//Assign values to array elements of reference types;
        mans[1]=m2;//Assign values to array elements of reference types;
    }
}

7.2.2 Initialization

There are three ways to initialize arrays: static initialization, dynamic initialization and default initialization. The following three ways are explained separately.

1. initiate static
   In addition to using new keywords to generate arrays, you can also define arrays at the same time allocate space and assign values to array elements.

[Example 7-4] Statically initialized array

int[] a = { 1, 2, 3 };// Statically initialize arrays of basic types;
Man[] mans = { new Man(1, 1), new Man(2, 2) };// Statically initialize the reference type array;

1. dynamic initialization

Array definitions are separated from assigning space to and assigning values to array elements.

[Example 7-5] Dynamic initialization array

int[] a1 = new int[2];//Initialize the array dynamically and allocate space first.
a1[0]=1;//Assign values to array elements;
a1[1]=2;//Assign values to array elements;

1. Default initialization of arrays.
   An array is a reference type whose elements are equivalent to instance variables of a class, so once the array is allocated space, each element of the array is implicitly initialized in the same way as the instance variables.

Default initialization of [Example 7-6] arrays

int a2[] = new int[2]; // Default values: 0, 0
boolean[] b = new boolean[2]; // Default values: false,false
String[] s = new String[2]; // Default values: null, null

Traversal of 7.3.1 Array

The legal interval of subscript of array element: [0,length-1]. We can traverse the elements in the array by subscripts, and we can read the values of the elements or modify the values of the elements when traversing.

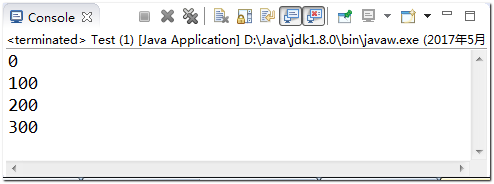
[Example 7-7] Initialize and read arrays using loop traversal

public class Test {
    public static void main(String[] args) {
        int[] a = new int[4];
        //Initialize the values of array elements
        for(int i=0;i<a.length;i++){
            a[i] = 100*i;
        }
        //Read the value of the element
        for(int i=0;i<a.length;i++){
            System.out.println(a[i]);
        }
    }
}

Implementation results:

7.3.2 for-each cycle

Enhanced for loop for-each is a new addition to JDK 1.5, which is dedicated to reading all elements in an array or collection, i.e., traversing the array.

[Example 7-8] Enhanced for loop

public class Test {
    public static void main(String[] args) {
        String[] ss = { "aa", "bbb", "ccc", "ddd" };
        for (String temp : ss) {
            System.out.println(temp);
        }
    }
}

results of enforcement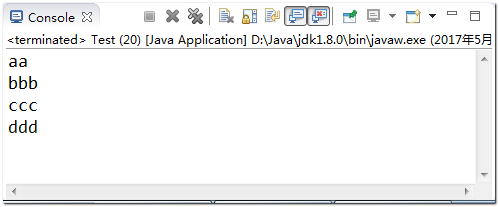

Matters needing attention

1. for-each enhances for loops that cannot modify the value of an element in an array while traversing the array.
2. for-each is only applicable to traversal and does not involve operations related to indexing (subscripts).

Copy of 7.3.3 Array

The System class also contains a static void array copy (object src, int srcpos, object dest, int destpos, int length) method, which assigns the element values in the Src array to the elements of the dest array, in which srcpos specifies how many elements of the SRC array are assigned to the elements of the dest array, and the length parameter specifies how many elements of the SRC array are assigned to the elements of the SRC array.

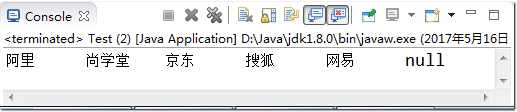
public class Test {
    public static void main(String args[]) {
        String[] s = {"Ali","Ada Tam","JD.COM","Sohu","NetEase"}; 
        String[] sBak = new String[6];
        System.arraycopy(s,0,sBak,0,s.length);
        for (int i = 0; i < sBak.length; i++) {
            System.out.print(sBak[i]+ "\t");
        }
    }
}

Implementation results:

7.3.4 java.util.Array class

The java.util.Arrays class provided by JDK contains common array operations for our daily development. The Arrays class contains common operations such as sorting, finding, filling, and printing content.

[Example 7-10] Print arrays

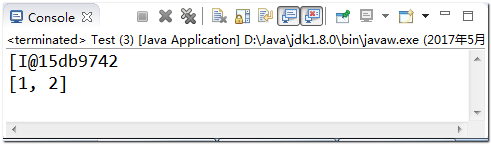
import java.util.Arrays;
public class Test {
    public static void main(String args[]) {
        int[] a = { 1, 2 };
        System.out.println(a); // Print the values referenced by the array;
        System.out.println(Arrays.toString(a)); // Print the value of the array element;
    }
}

Implementation results:

Rookie minefield

The Arrays.toString() method here is a static method of the Arrays class, not the toString() method of Object mentioned earlier.

[Example 7-11] Sorting of array elements

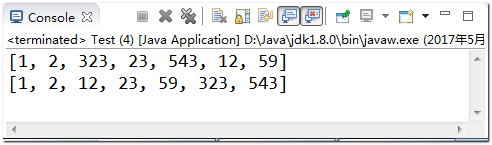
import java.util.Arrays;
public class Test {
    public static void main(String args[]) {
        int[] a = {1,2,323,23,543,12,59};
        System.out.println(Arrays.toString(a));
        Arrays.sort(a);
        System.out.println(Arrays.toString(a));
    }
}

results of enforcement

[Example 7-12] Array elements are sorting of reference types (application of Comparable interface)

import java.util.Arrays;
public class Test {
    public static void main(String[] args) {
        Man[] msMans = { new Man(3, "a"), new Man(60, "b"), new Man(2, "c") };
        Arrays.sort(msMans);
        System.out.println(Arrays.toString(msMans));
    }
}
 
class Man implements Comparable {
    int age;
    int id;
    String name;
 
    public Man(int age, String name) {
        super();
        this.age = age;
        this.name = name;
    }
 
    public String toString() {
        return this.name;
    }
 
    public int compareTo(Object o) {
        Man man = (Man) o;
        if (this.age < man.age) {
            return -1;
        }
        if (this.age > man.age) {
            return 1;
        }
        return 0;
    }
}

[Example 7-13] Dichotomy search

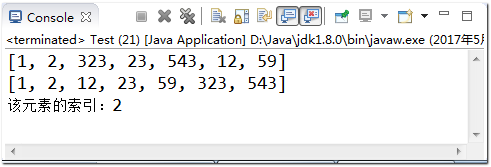
import java.util.Arrays;
public class Test {
    public static void main(String[] args) {
        int[] a = {1,2,323,23,543,12,59};
        System.out.println(Arrays.toString(a));
        Arrays.sort(a);   //When using dichotomy, the array must be sorted first.
        System.out.println(Arrays.toString(a));
        //Returns the new index position after sorting, if the negative number is not found.
        System.out.println("Index of this element:"+Arrays.binarySearch(a, 12)); 
    }
}

Implementation results:

[Example 7-14] Array Filling

import java.util.Arrays;
public class Test {
    public static void main(String[] args) {
        int[] a= {1,2,323,23,543,12,59};
        System.out.println(Arrays.toString(a));
        Arrays.fill(a, 2, 4, 100);  //Replace the 2-4 indexed elements with 100;
        System.out.println(Arrays.toString(a));
    }
}

Implementation results:

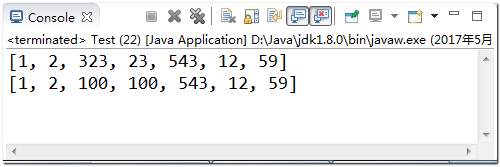
7.4 Multidimensional Array

Multidimensional arrays can be seen as arrays of Yuan Xu. There can be two-dimensional, three-dimensional, or even more dimensional arrays, but they are rarely used in actual development. Up to two-dimensional arrays (after learning containers, we usually use containers, but two-dimensional arrays are rarely used).

Declarations of two-dimensional arrays [Example 7-15]

public class Test {
    public static void main(String[] args) {
        // Declarations and initializations of multidimensional arrays in Java should be done in the order from low to high dimensions.
        int[][] a = new int[3][];
        a[0] = new int[2];
        a[1] = new int[4];
        a[2] = new int[3];
        // int a1[][]=new int[][4]; //Illegal
    }
}

[Example 7-16] Static initialization of two-dimensional arrays

public class Test {
    public static void main(String[] args) {
        int[][] a = { { 1, 2, 3 }, { 3, 4 }, { 3, 5, 6, 7 } };
        System.out.println(a[2][3]);
    }
}

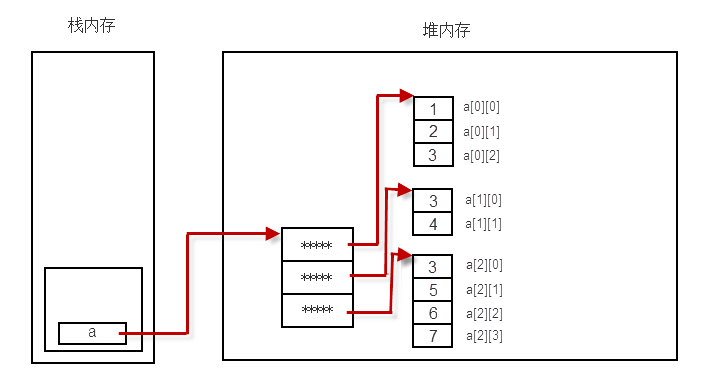
Dynamic initialization of two-dimensional arrays

import java.util.Arrays;
public class Test {
    public static void main(String[] args) {
        int[][] a = new int[3][];
        // A [0]= {1,2,5}; // Error, initialization without declared type
        a[0] = new int[] { 1, 2 };
        a[1] = new int[] { 2, 2 };
        a[2] = new int[] { 2, 2, 3, 4 };
        System.out.println(a[2][3]);
        System.out.println(Arrays.toString(a[0]));
        System.out.println(Arrays.toString(a[1]));
        System.out.println(Arrays.toString(a[2]));
   

Implementation results:

[Example 7-18] Get the array length

//Gets the length of the first dimensional array of a two-dimensional array.
System.out.println(a.length);
//Gets the length of the first array in the second dimension.
System.out.println(a[0].length);

7.5 Array Storage Table Data

Tabular data model is the most common model in the computer world. It can be said that all the data you see on the Internet are essentially "tables", which are just tables applied to each other.

We looked at the table and found that each row could be stored using a one-dimensional array:

Object[] a1 = {1001,"Gao Qi",18,"lecturer","2006-2-14"};
Object[] a2 = {1002,"Gao Xiao Qi",19,"Assistant","2007-10-10"};
Object[] a3 = {1003,"Gao Xiao Qin",20,"Headmaster","2008-5-5"};

Matters needing attention

Here the basic data type "1001" is not an Object object in essence. The Java compiler automatically boxes the basic data types into wrapper class objects. You will understand the packaging in the next chapter.

So we just need to define a two-dimensional array and put the above three arrays into it:

Object[][]  emps = new Object[3][];
emps[0] = a1;
emps[1] = a2;
emps[2] = a3;

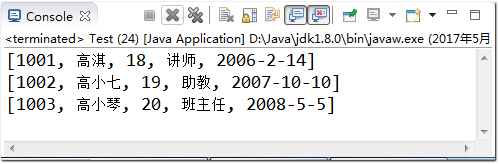
[Example 7-19] Two-dimensional arrays store table data

import java.util.Arrays;
public class Test {
    public static void main(String[] args) {
        Object[] a1 = {1001,"Gao Qi",18,"lecturer","2006-2-14"};
        Object[] a2 = {1002,"Gao Xiao Qi",19,"Assistant","2007-10-10"};
        Object[] a3 = {1003,"Gao Xiao Qin",20,"Headmaster","2008-5-5"};
        Object[][]  emps = new Object[3][];
        emps[0] = a1;
        emps[1] = a2;
        emps[2] = a3;
        System.out.println(Arrays.toString(emps[0]));
        System.out.println(Arrays.toString(emps[1]));
        System.out.println(Arrays.toString(emps[2]));  
    }
}

7.6.1 Foundation Algorithms for Bubble Sorting

Bubble sorting is the most commonly used sorting algorithm. It is also very common in written tests. It can be said that skilled hand-written bubble sorting algorithm is the basic accomplishment.

The algorithm repeatedly visits the columns to be sorted, compares two elements at a time, and swaps them if their order is wrong, so that the larger elements will slowly float to the top of the array through the swap.

The bubble sorting algorithm operates as follows:

1. Compare adjacent elements. If the first one is bigger than the second one, exchange the two.
2. Do the same work for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end. At this point, the last element should be the largest number.
3. Repeat the above steps for all elements except the last one.
4. Continue repeating the above steps for fewer and fewer elements each time until no pair of numbers need to be compared.

You can use the above idea to rearrange the following people from low to high:

Basic Algorithms for Bubble Sorting

import java.util.Arrays;
public class Test {
    public static void main(String[] args) {
        int[] values = { 3, 1, 6, 2, 9, 0, 7, 4, 5, 8 };
        bubbleSort(values);
        System.out.println(Arrays.toString(values));
    }
 
    public static void bubbleSort(int[] values) {
        int temp;
        for (int i = 0; i < values.length; i++) {
            for (int j = 0; j < values.length - 1 - i; j++) {
                if (values[j] > values[j + 1]) {
                    temp = values[j];
                    values[j] = values[j + 1];
                    values[j + 1] = temp;
                }
            }
        }
    }
}

Implementation results:

7.6.2 Bubble Sorting Optimization Algorithms

In fact, we can optimize the bubble sorting algorithm of 7.6.1, based on the following characteristics of bubble sorting:

1. The whole sequence is divided into two parts: the first is an unordered sequence, and the second is an ordered sequence.
2. Initially, the sequence is disordered and the ordered sequence is empty.
3. Each cycle can make the largest number in the disordered sequence last, (that is, the number of elements in the ordered sequence increases by 1), that is, it does not need to estimate the ordered sequence.
4. Each cycle begins with the first element of the sequence, comparing the two adjacent elements at one time to the end of the disordered sequence (rather than the end of the sequence); if the former is larger than the latter, exchange.
5. Determine whether the exchange of array elements occurs in each trip. If it does not occur, then the array has been ordered. There is no need to compare the number of subsequent trips. At this time, the comparison can be aborted.

[7-21] Bubble Sorting Optimization Algorithms

import java.util.Arrays;
public class Test1 {
    public static void main(String[] args) {
        int[] values = { 3, 1, 6, 2, 9, 0, 7, 4, 5, 8 };
        bubbleSort(values);
        System.out.println(Arrays.toString(values));
    }
    public static void bubbleSort(int[] values) {
        int temp;
        int i;
        // Outer loop: n elements are sorted, and at most n-1 loops are required
        for (i = 0; i < values.length - 1; i++) {
            // Define a Boolean-type variable to mark whether the array has reached an ordered state
            boolean flag = true;
    /*Inner loop: Each loop compares the first two elements of a sequence to the last of an unordered array*/
            for (int j = 0; j < values.length - 1 - i; j++) {
                // If the former element is larger than the latter, the values of the two elements are exchanged.
                if (values[j] > values[j + 1]) {
                    temp = values[j];
                    values[j] = values[j + 1];
                    values[j + 1] = temp;
                       //Exchange occurred in this trip, which indicates that the array is in disorder and needs to be compared further.
                    flag = false;
                }
            }
           //Judge whether the array is ordered according to the value of the tag quantity. If it is ordered, it exits; if it is disordered, it continues to loop.
            if (flag) {
                break;
            }
        }
    }
}

Implementation results:

7.7 Dichotomy Search

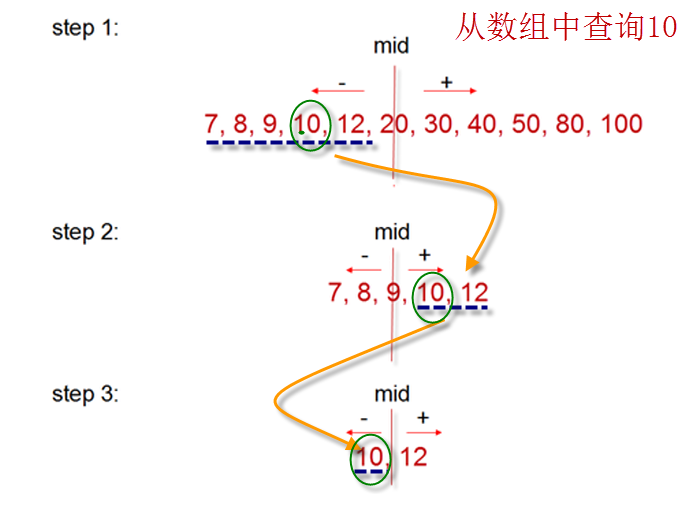
binary serach is also called folded half search. The basic idea of bipartite search is to store elements in arrays orderly from small to large. Firstly, the given value key is compared with the key of elements in the middle position of arrays. If it is equal, the search is successful.

Otherwise, if the key is small, the binary search will continue in the first half of the array.
If the key is large, the binary search is continued in the latter half of the array.

In this way, the search interval will be reduced by half after a price comparison, and the search will continue until the search is successful or the search is unsuccessful.

Binary retrieval is an efficient retrieval method. For example, we need to query 10 elements in the array [7, 8, 9, 10, 12, 20, 30, 40, 50, 80, 100], as follows:

[Example 7-22] Dichotomy search

import java.util.Arrays;
public class Test {
    public static void main(String[] args) {
        int[] arr = { 30,20,50,10,80,9,7,12,100,40,8};
        int searchWord = 20; // The number to be looked up
        Arrays.sort(arr); //Before searching by dichotomy, it is necessary to sort array elements.
        System.out.println(Arrays.toString(arr));
        System.out.println(searchWord+"Index of elements:"+binarySearch(arr,searchWord));
    }
 
    public static int binarySearch(int[] array, int value){
        int low = 0;
        int high = array.length - 1;
        while(low <= high){
            int middle = (low + high) / 2;
            if(value == array[middle]){
                return middle;         //Returns the index location of the query
            }
            if(value > array[middle]){
                low = middle + 1;
            }
            if(value < array[middle]){
                high = middle - 1;
            }
        }
        return -1;     //The above loop is complete, indicating that it is not found, return - 1
    }
}

summary

1. Arrays are the same type of data and ordered sets.
2. Four basic characteristics of arrays:

• Its length is fixed.
• Its elements must be of the same type
• Array variables belong to the reference type
• Basic data types and reference data types can be stored

1. One-Dimensional Combination Declarations

• type[] arr_name; (This is recommended)
• type arr_name[]；

1. Array initialization, dynamic initialization and default initialization.
2. Array length: Array name. lennth, subscript legal interval [0, array name. length-1].
3. Array copy: The static void array copy (object src, int srcpos, object dest, int destpos, int length) method in the System class.
4. Common class java.util.Array in Array Grass

• Print arrays: Arrays. toString (array name);
• Array sorting: Arrays.sort (array name);
• Binary Search: Arrays. binary Search

1. Declarations of two-dimensional arrays

• type[][]arr_name=new type[length][]；
• type arr_name[][]=new type[length][length]；