Then in the previous section, we continued to study functions

Function recursion

What is recursion?

1. Concept: the programming skill of program calling itself is called recursion. As an algorithm, recursion is widely used in programming languages. A process or function has a method to call itself directly or indirectly in its definition or description. It usually transforms a large and complex problem layer by layer into a smaller problem similar to the original problem. The recursive strategy can describe the multiple repeated calculations required in the problem-solving process with only a small number of programs, which greatly reduces the amount of code of the program. The main way of thinking about recursion is to make big things small
2. Recursion is simply a function calling itself

Let's go to the next simplest call function in history, but this is a wrong demonstration

#include<stdio.h>
int main()
{
 printf("hehe\n");//Dead cycle hehe
 main();//The main function calls itself
 return 0;
}

Exercise 1
Receive an integer value (unsigned) and print each bit of it in order. For example: input: 1234, output 1 2 3 4.
Integration ideas:
1234%10=4
1234/10=123%10=3
123/10=12%10=2
12/10=1%10=1

#include<stdio.h>
void print(unsigned int n)
{
 if (n > 9)
 {
  print(n / 10);
 }
 printf("%d ", n % 10);
}
int main()
{
 unsigned int num = 0;
 scanf("%u", &num);
 //Recursion: functions call themselves
  print(num);//The print function prints each bit of the number in the parameter section
}

The code analysis is shown in the figure below: layer by layer call

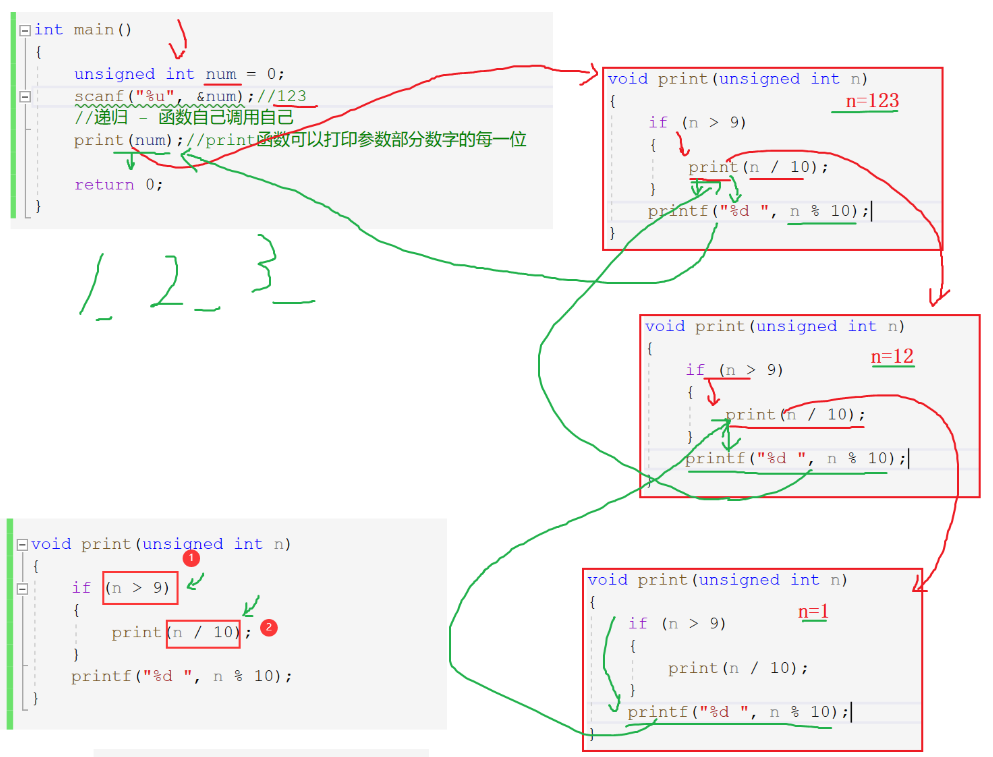
Two necessary conditions for recursion: two conditions that must be met
1. There is a constraint. When this constraint is met, recursion will not continue.
2. After each recursive call, it gets closer and closer to this limit.

However, it may not be successful if the two conditions are met. For example, the following code has a stack overflow

#include<stdio.h>
void test(int n)
{
 if (n < 10000)
 {
  test(n + 1);
 }
}
int main()
{
 test(1);
 return 0;
}

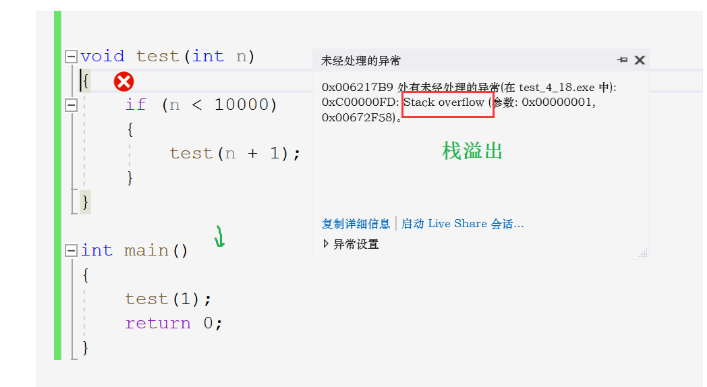
Therefore, when writing code, you should pay attention to:
1. No dead recursion. There must be a jump out condition. Each recursion must be close to the jump out condition
2. The recursion level cannot be too deep, otherwise stack overflow will occur

Exercise 2: writing a function does not allow the creation of temporary variables. Find the length of the string.

This code creates a temporary variable count to count, which does not meet the requirements of the topic

#include<stdio.h>
int my_strlen(char* str)//The pass parameter passes the address of the first element of the array, which is a character 'b'
{
 int count = 0;
 while (*str != '\0')
 {
  count++;//Calculation length
  str++;//str go back
 }
 return count;
}
int main()
{
 char arr[] = "bit";
 printf("%d\n",my_strlen(arr));
 return 0;
}

This code meets the requirements of the topic!!!
Integration of ideas:

#include<stdio.h>
int my_strlen(char* str)//The parameter passed is the address of the first element of the array. The first element of the array is a character 'b', so what arr passed is actually the address of b
{
 if (*str != '\0')
  return 1 + my_strlen(str + 1);
 else
  return 0;
}
int main()
{
 char arr[] = "bit";
 //The memory is actually ['b']['i']['t'][''b '] ['I'] ['t '] [' \ 0  ']
 printf("%d\n", my_strlen(arr));
 return 0;
}

The code idea is analyzed as follows:

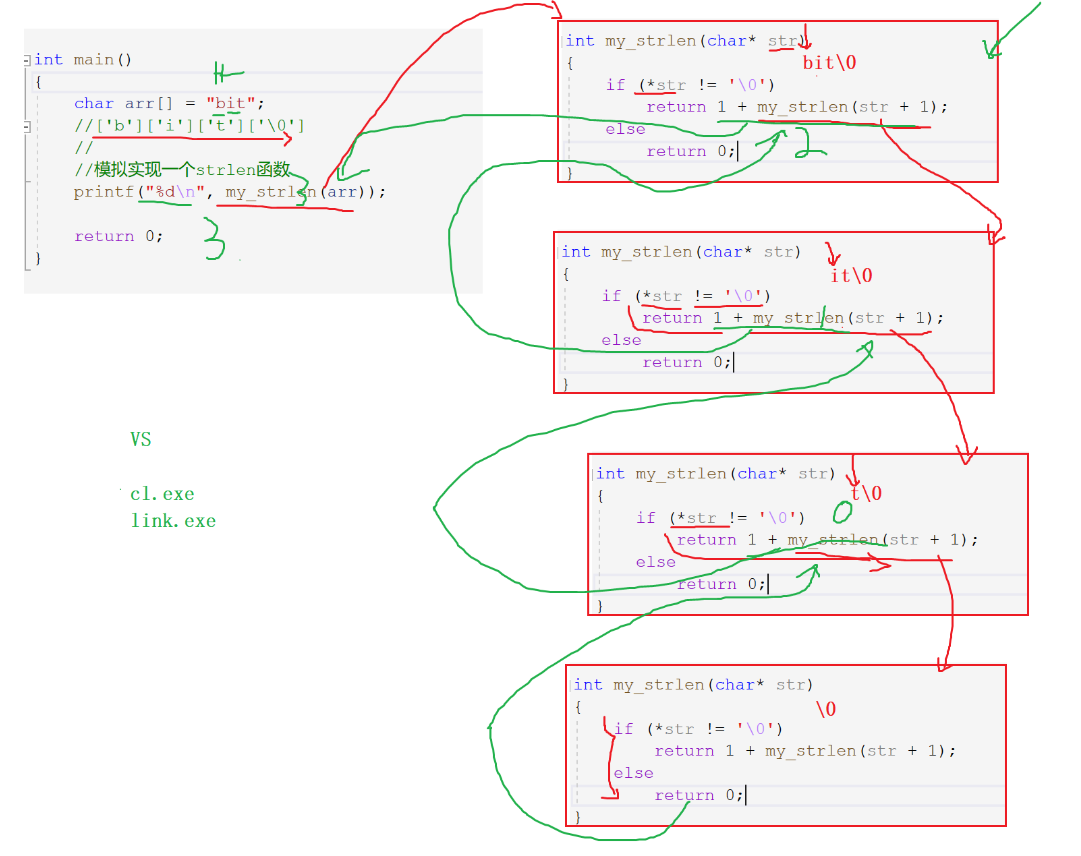
Conclusion: Although there are few codes, the logic is very complex and needs to be analyzed slowly and carefully; It embodies the characteristics of recursion and a large number of repeated calculations with a small amount of code

Recursion and iteration

Exercise 3: Factoring n. (overflow is not considered)
n!:123*...n

#include<stdio.h>
int main()
{
 int n = 0;
 scanf("%d", &n);
 int i = 0;
 int ret = 1;
 //Loop is an iterative way
 for (i = 1; i <= 0; i++)
 {
  ret = ret*i;
 }
 printf("%d\n", ret);
  return 0;
}

#include<stdio.h>
int Fac(int n)
{
 if (n <= 1)
  return 1;
 else
  return n*Fac(n - 1);
}
int main()
{
 int n = 0;
 scanf("%d", &n);
 int ret = Fac(n);
 printf("%d\n", ret);
 return 0;
}

There are some functions; It can be implemented iteratively (loop) or recursively
Exercise 4: find the nth Fibonacci number. (overflow is not considered)
What is Fibonacci number?
1 1 2 3 5 8 13 21 34 55... (the sum of the first two numbers equals the third number)
Fibonacci number formula:

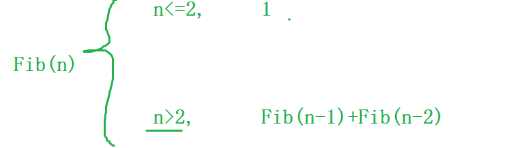
#include<stdio.h>
//Recursion can be solved, but the efficiency is too low
int count = 0;
int Fib(int n)
{
 if (n == 3)//Count the number of computers for the third Fibonacci number
  count++;
 if (n <= 2)
  return 1;
 else
  return Fib(n - 1) + Fib(n - 2);
}
int main()
{
 int n = 0;
 scanf("%d", &n);
 int ret = Fib(n);
 printf("%d\n", ret);//If the number is large, it needs to run for a long time
 printf("count=%d\n", count);
 return 0;
}

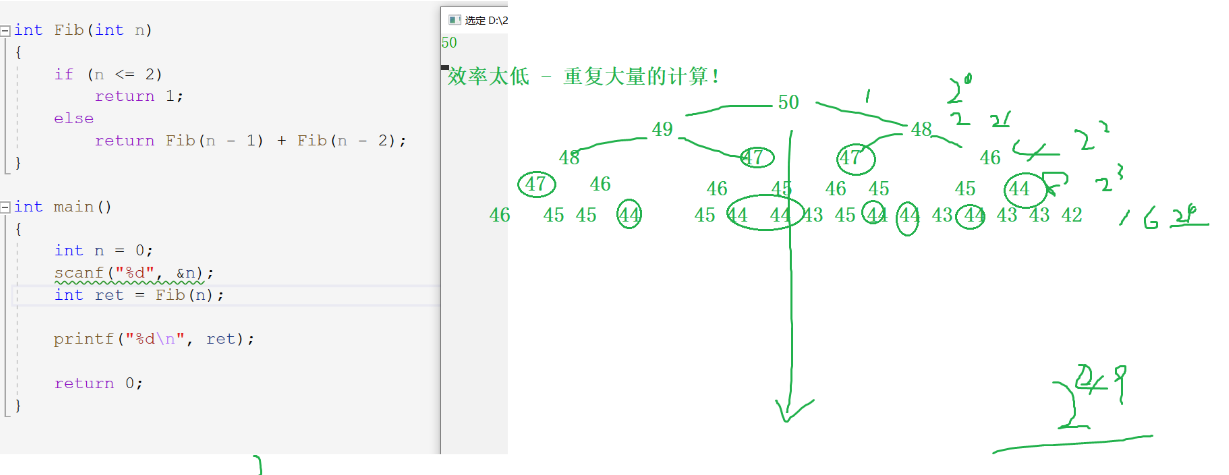
Summary: we can find that many calculations are repeated during the call of fib function.
This problem can be solved in a circular or iterative manner
At this time, the efficiency is very high. Even if a large number is input, the result can be obtained quickly (but when a large number is input, the calculation result is wrong)

#include<stdio.h>
int Fib(int n)
{
 int a = 1;
 int b = 1;
 int c = 1;
 while (n>2)
 {
  c = a + b;
  a = b;
  b = c;
  n--;
 }
 return c;
}
int main()
{
 int n = 0;
 scanf("%d", &n);
 int ret = Fib(n);
 printf("%d\n", ret);
 return 0;
}

Conclusion: it is not suitable to find the nth Fibonacci number by recursive method, but by iterative method