Stack implementation synthesis calculator (infix expression)

Thought analysis:

1. We need two stacks: number stack and symbol stack to define an index index index index to traverse the expression
2. Traverse to a number, then enter the number stack
3. Traverse to a symbol. If the symbol stack is empty, it will be put into the symbol stack;
   If the symbol stack is not empty: if the currently traversed symbol priority is less than or equal to the symbol priority in the symbol stack, two numbers will be generated from the pop in the data stack, one symbol will be generated from the pop in the symbol stack for operation, and then the operation result will be input into the data stack, and the currently traversed symbol will be input into the symbol stack; if the currently traversed symbol priority is greater than the symbol priority in the symbol stack, then Put the symbol directly into the symbol stack.
4. After the expression traversal is completed, pop values from the data stack and symbol stack are calculated in order
5. There will be only one number in the final stack, that is, the result of the operation.

Code implementation:

package com.datastructures.stack;

public class Calculator {
    public static void main(String[] args) {
        String expression = "70+2*6-2";
        //Create two stacks
        ArrayStack2 numStack = new ArrayStack2(10);
        ArrayStack2 operStack = new ArrayStack2(10);
        int index = 0;//Used to scan expressions
        int num1 = 0;
        int num2 = 0;
        int oper = 0;
        int res = 0;
        char ch = ' ';
        String keepNum = "";//Used to splice multiple bits
        while (true) {
            ch = expression.substring(index, index + 1).charAt(0);
            if (operStack.isOper(ch)) {//Scan to yes symbol
                if (!operStack.isEmpty()) {
                    //If the currently traversed symbol priority is less than or equal to the symbol priority in the symbol stack,
                    //Then pop two numbers from the number stack and pop a symbol from the symbol stack for operation,
                    // Then, the operation results are put into the data stack, and the currently traversed symbols are put into the symbol stack;
                    if (operStack.priority(ch) <= operStack.priority(operStack.peek())) {
                        num1 = numStack.pop();
                        num2 = numStack.pop();
                        oper = operStack.pop();
                        res = numStack.cal(num1, num2, oper);
                        numStack.push(res);
                        operStack.push(ch);

                    } else {
                        //If * * the currently traversed symbol priority is higher than the symbol priority * * in the symbol stack, put the symbol directly into the symbol stack
                        operStack.push(ch);
                    }
                } else {
                    //If the symbol stack is empty, enter the symbol stack;
                    operStack.push(ch);
                }

            } else {//Scan to a number
                //numStack.push(ch-48);
                //Number of processing bits:
                // When index scans a number, scan one bit later. If the latter bit is a symbol, put the number into the data stack. Otherwise, continue scanning
                // You need to define a variable string to concatenate numbers

                //If ch is already the last bit of expression, it will be pushed directly
                keepNum += ch;
                if (index == expression.length() - 1) {
                    numStack.push(Integer.parseInt(keepNum));

                } else {

                    if (operStack.isOper(expression.substring(index + 1, index + 2).charAt(0))) {
                        numStack.push(Integer.parseInt(keepNum));
                        //Be careful to empty keepNum
                        keepNum = "";
                    }
                }
            }
            index++;
            if (index >= expression.length()) {
                break;

            }
        }
        //After the expression traversal is completed, pop values from the data stack and symbol stack are calculated in order
        while (true) {
            if (operStack.isEmpty()) {
                break;
            }
            num1 = numStack.pop();
            num2 = numStack.pop();
            oper = operStack.pop();
            res = numStack.cal(num1, num2, oper);
            numStack.push(res);
        }
        System.out.printf("expression%s The result is:%d", expression, numStack.pop());

    }


}

class ArrayStack2 {
    private int maxSize;//Maximum stack capacity
    private int[] stack;//Data defining an array stack exists in the array
    private int top = -1;//Point to top of stack

    public ArrayStack2(int maxSize) {
        this.maxSize = maxSize;
        stack = new int[maxSize];
    }

    //Stack full
    public boolean isFull() {
        return top == maxSize - 1;
    }

    //Stack empty
    public boolean isEmpty() {
        return top == -1;
    }

    //Display the current stack top element
    public int peek() {
        return stack[top];
    }

    //Push 
    public void push(int data) {
        if (isFull()) {
            System.out.printf("Stack full, unable to enter");
            return;
        } else {
            top++;
            stack[top] = data;
        }
    }

    //Out of the stack
    public int pop() {
        if (isEmpty()) {
            throw new RuntimeException("Stack empty");
        } else {
            int value = stack[top];
            top--;
            return value;
        }
    }

    //Display stack
    public void show() {
        if (isEmpty()) {
            throw new RuntimeException("Stack empty");
        } else {
            for (int i = top; i >= 0; i--) {
                System.out.printf("stack[%d]=%d\n", i, stack[i]);
            }
        }
    }

    //The priority of the return operator specifies that the higher the number, the higher the priority
    public int priority(int oper) {
        if (oper == '*' || oper == '/') return 1;
        else if (oper == '+' || oper == '-') return 0;
        else return -1;//Suppose there are only + - * / four symbols at present
    }

    //Judge whether it is a symbol
    public boolean isOper(int oper) {
        return oper == '+' || oper == '-' || oper == '*' || oper == '/';
    }

    //Define operation rules
    public int cal(int num1, int num2, int oper) {
        int res = 0;
        switch (oper) {
            case '+':
                res = num1 + num2;
                break;
            case '-':
                res = num2 - num1;
                break;
            case '*':
                res = num1 * num2;
                break;
            case '/':
                res = num2 / num1;
                break;
            default:
                break;
        }
        return res;
    }

}

Code implementation of the reverse Polish Calculator: (only integers are supported)

Prefixes: right to left calculation
Suffixes: left to right calculation

package com.datastructures.stack;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class PolandNotation {
    public static void main(String[] args) {
        //Define an inverse Polish expression (3 + 4) * 5-6 = > 3 4 + 5 * 6-
        String suffixExpression = "3 4 + 5 * 6 -";
        List<String> rpnList = getListString(suffixExpression);
        System.out.println("rpnList=" + rpnList);
        int res=cal(rpnList);
        System.out.println("The calculation results are as follows:"+res);
    }

    public static List<String> getListString(String suffixExpression) {
        //Put numbers and symbols in expressions into ArrayList
        String[] split = suffixExpression.split(" ");
        List<String> list = new ArrayList<String>();
        for (String ele : split) {
            list.add(ele);
        }
        return list;
    }

    /*
        Calculation steps:
        1)Scan left to right to stack 3 and 4
        2)When the + operator is encountered, pop up the top element 4 and the secondary top element 3, calculate the value of 3 + 4 and stack it
        3)5 Push 
        4)When encountering * pop-up 5,7 calculation results and stack
        5)6 Push 
        6)Encounter - pop up 35,6 calculation results
    */
    public static int cal(List<String> ls) {
        Stack<String> stack = new Stack<>();
        //Traversal list set
        for (String i : ls) {
            if (i.matches("\\d+")) {
                stack.push(i);
            } else {
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res = 0;
                if (i.equals("+")) {
                    res = num1 + num2;
                } else if (i.equals("-")) {
                    res = num1 - num2;
                } else if (i.equals("*")) {
                    res = num1 * num2;
                } else if (i.equals("/")) {
                    res = num1 / num2;
                }else{
                    throw new RuntimeException("Wrong operator!");
                }
                stack.push("" + res);
            }

        }
        return Integer.parseInt(stack.pop());
    }
}

Infix expression to suffix expression:

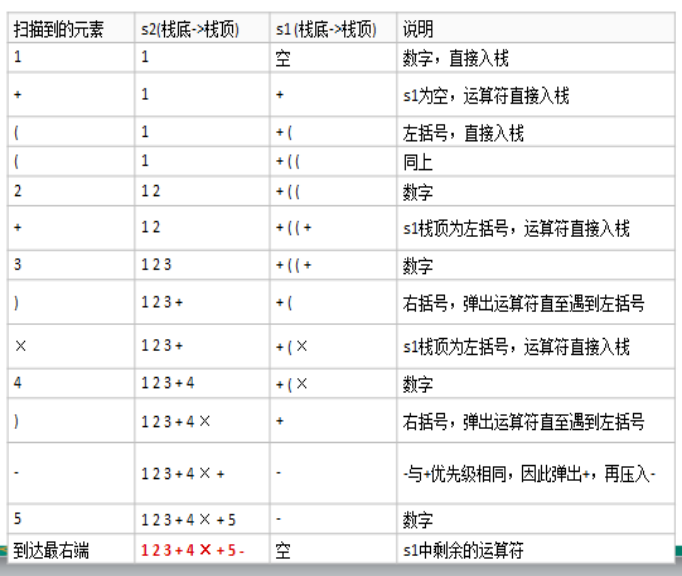
Infix expression 1 + ((2 + 3) × 4) - 5 =) suffix expression
Stack s2 - 5 + * 4 + 3 2 1 = > 1 2 3 + 4 * + 5-
Step:

1. Two stacks are initialized: operator stack s1 and stack s2 storing intermediate results;

2. Scan infix expression from left to right;

3. When the operands are encountered, press s2;

4. When an operator is encountered, compare its priority with s1 stack top operator:

   1. If s1 is empty, or the top of stack operator is left bracket "(", the operator will be directly pushed into the stack;
   2. Otherwise, if the priority is higher than the stack top operator, the operator will also be pressed into s1;
   3. Otherwise, pop up the operator at the top of s1 stack and press it into s2, then turn to 4.1 again to compare with the new operator at the top of s1 stack;

5. When parentheses are encountered:
   If it is the left bracket "(", press s1 directly
   If it is a right parenthesis ")", the operators at the top of s1 stack will pop up in turn, and press s2 until the left parenthesis is encountered. At this time, this pair of parentheses will be discarded

6. Repeat steps 2 through 5 until the far right of the expression

7. Pop up the remaining operators in s1 and press them into s2

8. Pop out the elements in s2 in turn and output. The reverse order of the result is the suffix expression corresponding to infix expression
   
   Code implementation:

package com.datastructures.stack;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class PolandNotation {
    public static void main(String[] args) {
        //1. Complete the function of converting infix expression to suffix expression 1 + ((2 + 3) * 4) - 5 = > 1 2 3 + 4 * + 5-
        //Because it is not convenient to operate the expression directly, first set "1 + ((2 + 3) * 4) - 5" = > the List corresponding to infix expression
        //That is, "1 + ((2 + 3) * 4) - 5" = > ArrayList [1, +, (, 2, +, 3,), *, 4,), -, 5]
        String expression = "1+((2+3)*4)-5";
        List<String> infixExpressionList = toInfixExpressionList(expression);
        System.out.println("Infix expression corresponding to List: "+infixExpressionList);
        List<String> suffixExpressionList = parseSuffixExpressionList(infixExpressionList);
        System.out.println("Corresponding to suffix expression List: "+suffixExpressionList);
        int res = cal(suffixExpressionList);
        System.out.println("The calculation results are as follows:"+res);

       /* //Define an inverse Polish expression (3 + 4) * 5-6 = > 3 4 + 5 * 6-
        String suffixExpression = "3 4 + 5 * 6 -";
        List<String> rpnList = getListString(suffixExpression);
        System.out.println("rpnList=" + rpnList);
        int res=cal(rpnList);
        System.out.println("The calculation result is: "+ res";*/
    }

    //2. Convert infix expression to corresponding list s = "1 + ((2 + 3) * 4) - 5" = > ArrayList [1, +, (, (, 2, +, 3,), *, 4,), -, 5]
    public static List<String> toInfixExpressionList(String s) {
        //Define a List to store the corresponding contents of infix expression
        List<String> ls = new ArrayList<String>();
        int i = 0;// Pointer, for traversal
        String str;//For multi bit splicing
        char c;//Every time a character is traversed, c is placed
        do {
            //If c is not a number, add ls directly
            if ((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57) {
                ls.add("" + c);
                i++;
            } else {//If c is a number, many bits need to be considered
                str = "";//Empty str
                while (i < s.length() && (c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57) {
                    str += c;//Splicing
                    i++;
                }
                ls.add(str);
            }
        } while (i < s.length());
        return ls;
    }

    //3. Convert the resulting infix expression List to the List corresponding to the suffix expression
    // That is, ArrayList [1, +, (, (, 2, +, 3,), *, 4,), -, 5] = > ArrayList [1,2,3, +, 4, *, +, 5, -]
    public static List<String> parseSuffixExpressionList(List<String> ls) {
        //1) Initialize two stacks: * * operator stack s1 and stack s2 storing intermediate results * *;
        Stack<String> s1 = new Stack<String>();//Operator stack s1
        //Because in the whole conversion process, s2 does not pop and needs to output s2 content in reverse order
        //Therefore, for convenience, the list < string > set can be used instead of the stack < string >
        List<String> s2 = new ArrayList<String>();//Store the list of intermediate results < string > S2;
        int index = 0;//Used to scan expressions
        //2) Traversal ls
        for (String item : ls) {
            //If it is a number, add s2
            if (item.matches("\\d+")) {
                s2.add(item);
            } else if (item.equals("(")) {
                s1.push(item);
            } else if (item.equals(")")) {
                //   If it is * * right bracket ")" * *, the operators at the top of s1 stack will pop up in turn, and s2 will be pressed in until the left bracket is encountered. In this case, the pair of brackets will be discarded
                while (!s1.peek().equals("(")) {
                    s2.add(s1.pop());
                }
                s1.pop();//Pop up "(" s1 to eliminate the bracket
            }else{
                //Pop up the operator at the top of s1 stack and press it into s2, then go to 4.1 again to compare it with the new operator at the top of s1 stack
                while(s1.size()!=0&&Operation.getValue(s1.peek())>=Operation.getValue(item)){
                    s2.add(s1.pop());
                }
                s1.push(item);
            }
        }
        //Pop up the remaining operators in s1 and add them to s2
        while (s1.size()!=0){
            s2.add(s1.pop());
        }
        return s2;//Because s2 is a List set, its sequential output is a suffix expression
    }


    public static List<String> getListString(String suffixExpression) {
        //Put numbers and symbols in expressions into ArrayList
        String[] split = suffixExpression.split(" ");
        List<String> list = new ArrayList<String>();
        for (String ele : split) {
            list.add(ele);
        }
        return list;
    }


      /*  Calculation steps:
        1)Scan left to right to stack 3 and 4
        2)When the + operator is encountered, pop up the top element 4 and the secondary top element 3, calculate the value of 3 + 4 and stack it
        3)5 Push 
        4)When encountering * pop-up 5,7 calculation results and stack
        5)6 Push 
        6)Encounter - pop up 35,6 calculation results*/

    public static int cal(List<String> ls) {
        Stack<String> stack = new Stack<>();
        //Traversal list set
        for (String i : ls) {
            if (i.matches("\\d+")) {
                stack.push(i);
            } else {
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res = 0;
                if (i.equals("+")) {
                    res = num1 + num2;
                } else if (i.equals("-")) {
                    res = num1 - num2;
                } else if (i.equals("*")) {
                    res = num1 * num2;
                } else if (i.equals("/")) {
                    res = num1 / num2;
                } else {
                    throw new RuntimeException("Wrong operator!");
                }
                stack.push("" + res);
            }

        }
        return Integer.parseInt(stack.pop());
    }
}
//Writing the Operation class can return the priority corresponding to the operator
class Operation{
    private static int ADD=1;
    private static  int SUB=1;
    private static  int MUL=2;
    private static int DIV=2;
    public static int getValue(String operation){
        int res=0;
        switch(operation){
            case "+":
                res=ADD;
                break;
            case "-":
                res=SUB;
                break;
            case "*":
                res=MUL;
                break;
            case "/":
                res=DIV;
                break;
            default:
                System.out.println("Operator does not exist!");
                break;
        }
        return res;
    }

}