Sorting algorithm refers to sorting one or more groups of data through a specific algorithm, so that the group of data conforms to ascending or descending order, which is convenient for calculation and screening, and improves the efficiency of data processing. Sorting algorithms can be implemented in a variety of computer languages. Here we implement several common sorting algorithms through Java.
Bubble sorting
Bubble sorting is a relatively simple sorting algorithm. Its principle is to compare the size of the front and rear elements in the array from beginning to end, exchange the position of the elements according to the size, and finally sort the elements in the array in ascending or descending order.
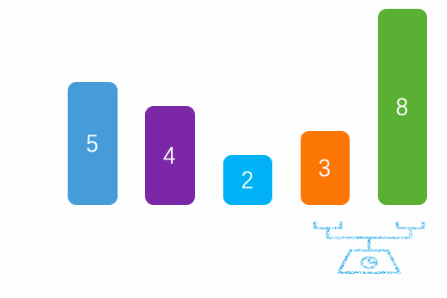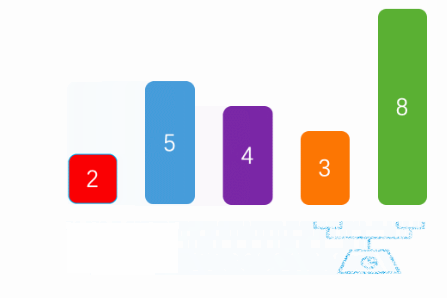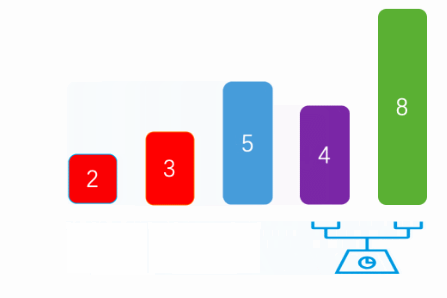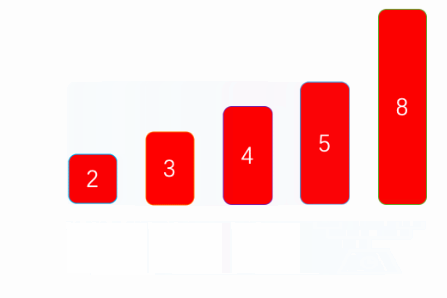
The above figure is an execution logic of bubble sorting.
First, we need to traverse the array. Assuming that there are N elements in the array, we need to traverse the array N-1 times to ensure that all elements are arranged in the right position. The last element does not need to be arranged because the other elements are already arranged.
After that, we will compare each element with other unordered elements, so as to adjust the of each element to the appropriate position. Compare the array from beginning to end. If the previous element is larger / smaller than the latter element, exchange the positions of the two elements until the element cannot be exchanged. At this point, the element will be in ascending / descending order.
Finally, we will repeat the second step. Each exchange step will be shorter until all elements are compared.
Bubble sorting is implemented by the following code.
public static void main(String[] args) {
int arr[] = {8, 5, 3, 2, 4};
//The outer loop controls the number of iterations
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length - i - 1; j++) {
//The inner loop controls the position of the exchange. Each loop obtains a maximum value. The front elements are exchanged when they are larger than the back elements
if (arr[j] > arr[j + 1]) { //Sort in ascending order, and '<' is in descending order
int temp = arr[j + 1];//Save current smaller value
arr[j + 1] = arr[j];//Assign a larger value to the next array element
arr[j] = temp;//Assign a smaller value to the current element
}
}
}
}
Bubble sorting is a stable algorithm with an average time complexity of O(n) ²) . In the above code, to bubble sort an array, two loops must be executed, which means n ² Secondary processing.
In fact, we can improve the bubbling algorithm to speed up its sorting processing speed. In the array, there are often cases where only a few elements need to be adjusted or the array itself is in ascending / descending order. At this time, the bubbling algorithm will still carry out the second layer cyclic exchange processing for the whole array, although most of the processing is unnecessary. In this case, we can add an execution condition to the first layer loop to restrict whether to execute the second layer loop. In this way, we can reduce unnecessary element exchange steps and improve sorting speed.
for (int i = 0; i < arr.length; i++) {
boolean aa = false;//Set aa as variable
System.out.print(1+" ");//Check whether the external circulation is executed
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = temp;
aa = true;//When the inner loop is executed, change the detection variable to true
System.out.print(0+" ");//Check whether the inner loop is executed
}
}
if (aa != true){//If the inner loop statement is not executed, it means that the current element does not need to be exchanged and jumps out of the inner loop
break;
}
}
By adding a boolean variable, we detect whether the program has experienced a second layer loop. If the second layer loop is not entered, it means that the currently processed element does not need to change its position, and it does not need to be compared with subsequent elements. Ideally, there is no need to exchange arrays of data, and only one traversal is required in bubble sorting, with a time complexity of O(n).
Select sort
Selective sorting is an unstable sorting algorithm, and its optimal and worst time complexity are O(n) ²).
The principle of selective sorting is to traverse the array and select the maximum / minimum value in the array, put the element in the head of the array, and process all the elements in the array in turn. The following figure shows the processing logic of selection sorting.
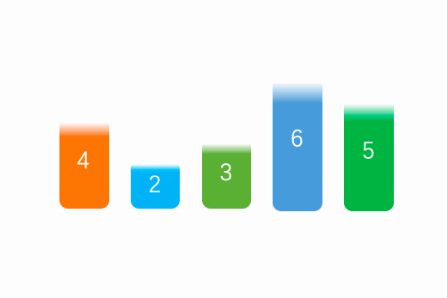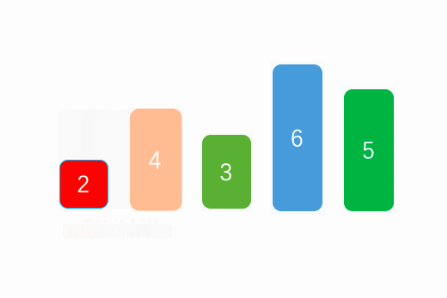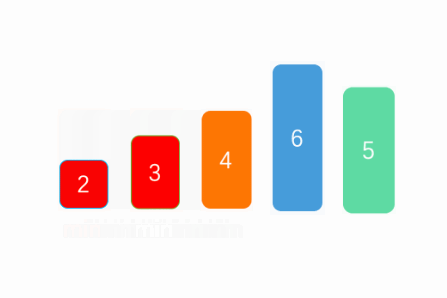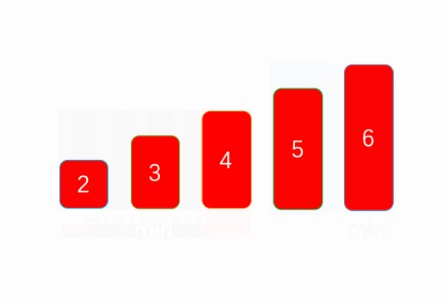
First, we will traverse the elements in the array. As with bubble sorting, you need to traverse N-1 times to process all the elements in the array.
After that, we have to choose the smallest element in the array. Defines the value and subscript of the current element as the minimum value and compares it with other elements through the second level loop. If the following element has smaller than the current element, the value and subscript of the new element are assigned to the minimum value. We iterate through the whole array through the second layer loop and find the minimum value.
Finally, we compare the current element with the minimum value. If the current element is not the minimum value, it is exchanged with the minimum value element. Repeat this step to sort the entire array.
The code for selecting sorting is as follows.
for(int i = 0;i<arr.length-1;i++){
int min = arr[i];
int minindex = i;
for(int j = i;j<arr.length;j++){
if(arr[j]<min){ //Select the current minimum number
min = arr[j];
minindex = j;
}
}
if(i != minindex){ //If i is not the smallest of the current element, it is exchanged with the found element
arr[minindex] = arr[i];
arr[i] = min;
}
}
Insert sort
Insertion sort is a stable sort algorithm, and its time complexity is O(n) ²). The insertion algorithm consists of two loops. The external loop controls the number of times the array is traversed, and the internal loop is responsible for looking forward for the insertion position in the array.

First, we need to set the number of times of array traversal, and take the second element in the array as the starting point (the first element cannot be inserted forward);
After that, we will save the value and subscript of the current element and judge whether the current element is smaller than the previous element;
Then, if the current element is smaller than the previous element, replace the value of the current subscript with the value of the previous subscript, move the subscript forward by 1 bit until the appropriate subscript position is found, and insert the value of the current element into the array.
Repeat the above process until the elements in the complete array are processed.
The implementation code is as follows.
for(int i = 1; i< arr.length; i++){
int index = i;
int value = arr[i];
while (index > 0 && value < arr[index -1]){
arr[index] = arr[index -1];
index--;
}
arr[index] = value;
}
The algorithm can also be optimized by setting the target variable, so that the space complexity of the algorithm in the best case (the array does not need to be sorted) is O(n). The optimization method is the same as bubble sorting. Set the target boolean variable in the outer loop, change its assignment in the inner loop, and detect whether the value of the target variable is changed after the inner loop, so as to jump out of the inner loop.
Shell Sort
The structure of Hill sort draws on the insertion sort, which also saves the insertion elements and looks for the insertion position. However, Hill sort needs to adjust the step size of insertion and comparison according to the number of cycles. Hill sorting is an unstable sorting algorithm with an average time complexity of O(nlog) ² n) , faster than direct insert sorting.
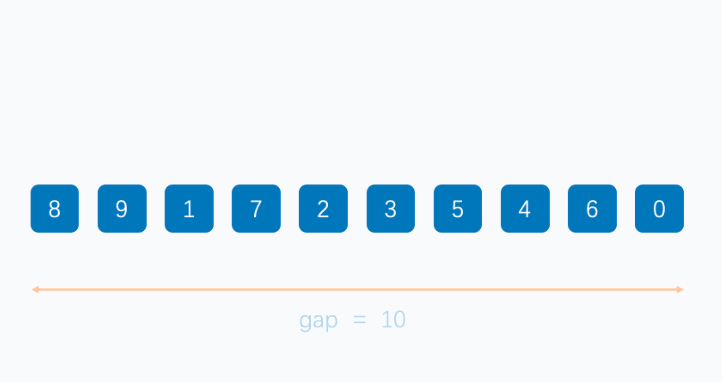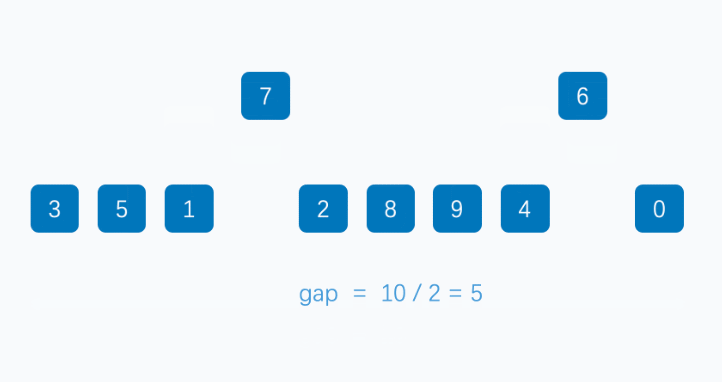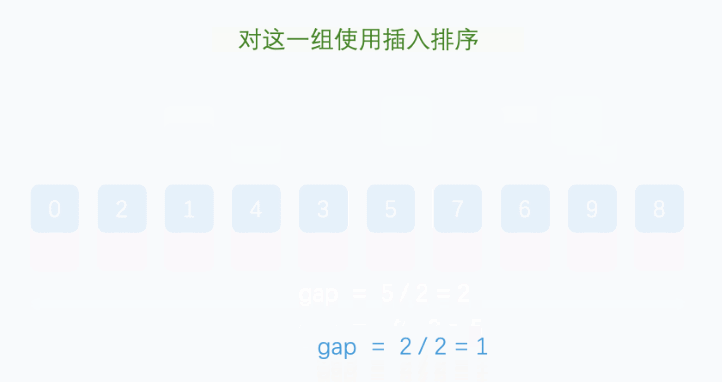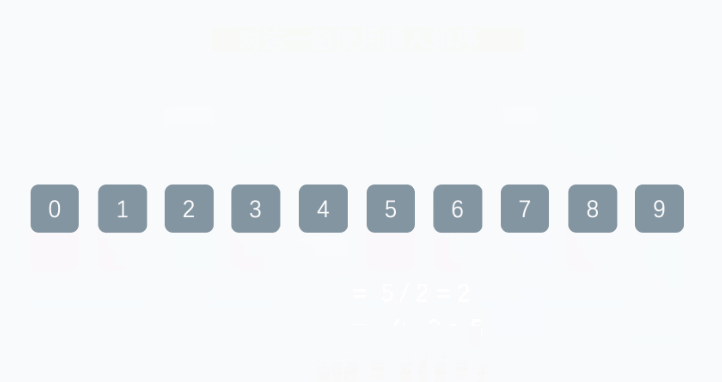
First, we need to set the step / interval of inserting data. The initial interval needs to perform modular operation on the array length (length/2). After each cycle, the step / = 2.
After that, we take the current step size as the starting position of the loop and save the subscript and value of the current element.
Then, we compare the size of the current element with that of the target element. If the current element is smaller than the target element, we will replace the index of the current element with the target element, move forward (in steps) until we find the appropriate index position, and insert the value of the current element into the array.
Repeat the above steps until all elements are adjusted.
The code implementation is as follows.
for(int gap = a.length/2;gap>0;gap/=2){
for(int i = gap;i<a.length;i++){
int index = i;
int insertValue = a[i];
while (index-gap >=0 && insertValue < a[index-gap]){
a[index] = a[index-gap];
index -= gap;
}
a[index] = insertValue;
}
}
Hill sort can also use bubble sort, but it is less efficient than insert based sort. If you're interested, you can explore,
Quick sort
The principle of quick sort is partition operation, that is, find a benchmark in an array and reorder according to the benchmark, so that the data on the left side of the benchmark is smaller than it and the data on the right side is larger than it. Then call this method recursively to insert the elements on both sides of the benchmark into the appropriate position, so as to realize array sorting. The average time complexity of fast scheduling is O(nlogn), which is O(n) in the worst case ²), It is an unstable but fast algorithm.
The implementation steps of quick sort are as follows:
1. Move the right pointer to make it less than the value of the reference point and move it to the left;
2. Move the left pointer to make it greater than or equal to the value of the reference point and move it to the right;
3. If the left pointer and the right pointer coincide, exchange the current element with the reference value;
4. If the left and right pointers have been adjusted and do not coincide, exchange the values in the left and right pointers;
5. Recursively call steps 1-4 to sort the values on the left and right sides of the benchmark respectively.
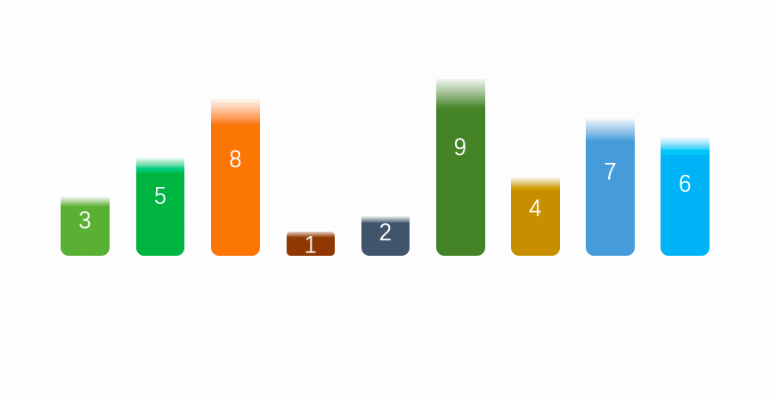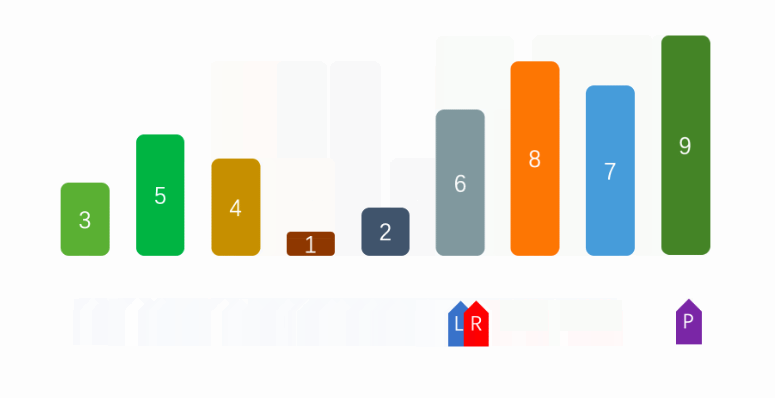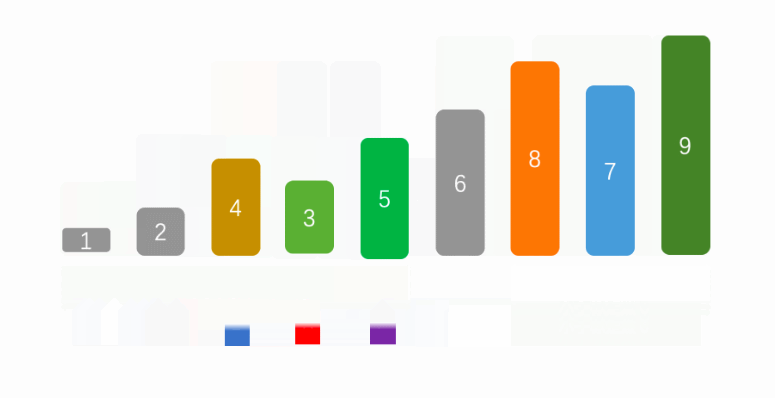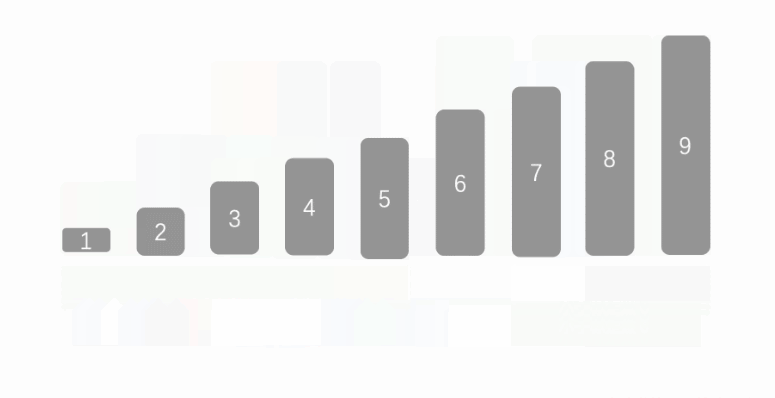
The code implementation is as follows.
public static void main(String []args) {
int[] a= {3, 2, 6, 1, 9, 5, 3, 6, 1, 7, 9, 2, 5};
quicksort(a, 0, a.length - 1);//Call the sorting method to set the starting point before and after the array
System.out.print(Arrays.toString(a));//Output sorted array
}
public static void quicksort(int []arr,int left, int right){
if(left>=right){//Set exit conditions for recursion
return;
}
int l = left;//Save left pointer start position
int r = right;//Save start position of right pointer
while(l<r){//The reference point is set to the starting position of the left pointer
while(l<r && arr[r]>=arr[left]){//When the data in the right pointer is less than the reference point, the right pointer moves left
r--;
}
while(l<r && arr[l]<=arr[left]){//When the data in the left pointer is less than the reference point, the left pointer moves to the right
l++;
}
if(r == l){//When the left and right pointers coincide, the value of the current element is exchanged with the value of the reference point
int tem = arr[r];
arr[r] = arr[left];
arr[left] = tem;
}else{//If the left and right pointers do not coincide after moving, the values of the left and right pointers are exchanged
int temp = arr[r];
arr[r] = arr[l];
arr[l] = temp;
}
}
//Recursion to sort the data on the left and right sides of the benchmark
quicksort(arr,left,l-1);
quicksort(arr,r+1,right);
}
}
Cardinality sort
Radix Sort is an extension of bucket sort. Its time complexity is O(d(n+r)): D is the number of bits, r is the base, and N is the number of original arrays. The efficiency of cardinality sorting is stable because its sorting process is independent of whether the array has order.
Different from other sorting algorithms, it is a non comparative sorting algorithm. Its principle is to divide the elements in the array into different groups (buckets) according to the number of bits, sort them according to the size of the number of bits, and then collect them into the original array after cyclic sorting.

The figure above is a process demonstration of cardinality sorting. For cardinality sorting, the algorithm logic is as follows:
1. Traverse the array, find out the maximum value in the array, get its digits, and set it as the number of times of this cardinality sorting;
2. Starting from the single digit, load the elements in the array into the two-dimensional array (bucket) in turn;
3. Fill the data in the two-dimensional array into the original array in order, and sort according to the next digit.
The code implementation is as follows.
public static void main(String[] args){
int[] arr = new int[]{4,6,3,34,67,993,57,2,56,843,36,80};
redixSort(arr);
System.out.print(Arrays.toString(arr));
}
public static void redixSort(int []a){
int [][]bucket = new int[10][a.length-1];//Specific elements stored in the bucket
int[] bucketCount = new int[10];//Set the number of elements stored in each bucket
int max = a[0];
for(int i = 1; i<a.length;i++){//Find the maximum
if(max<a[i])max = a[i];
}
int maxCount = (max+"").length();//Get the maximum number of digits
for (int i = 0;i<maxCount;i++){//Set the maximum number of digits as the number of cardinal sorting
for(int j = 0;j<a.length;j++){
//Call the pow method, divide the current element by the i power of 10, and take the remainder of 10 to obtain the value of the specified number of digits
int value = a[j]/(int)Math.pow(10,i)%10;
bucket[value][bucketCount[value]] = a[j];//Load the value into the specified location in the specified bucket
bucketCount[value]++;//Number of elements in this bucket + 1
}
int index = 0;
//Load the elements from the bucket back into the array
for(int x = 0;x< bucketCount.length;x++){
if (bucketCount[x]!=0){
for(int y = 0;y<bucketCount[x];y++){
a[index] = bucket[x][y];
index++;
}
}
bucketCount[x] = 0;//After data transfer, empty the data in the bucket
}
}
}
Merge sort
Merge sort is a sort operation using divide and conquer method, which divides the array into several small blocks and merges them into a new array in order. The best and worst time complexity of merge sorting is O(nlogn), which is a stable sorting algorithm.
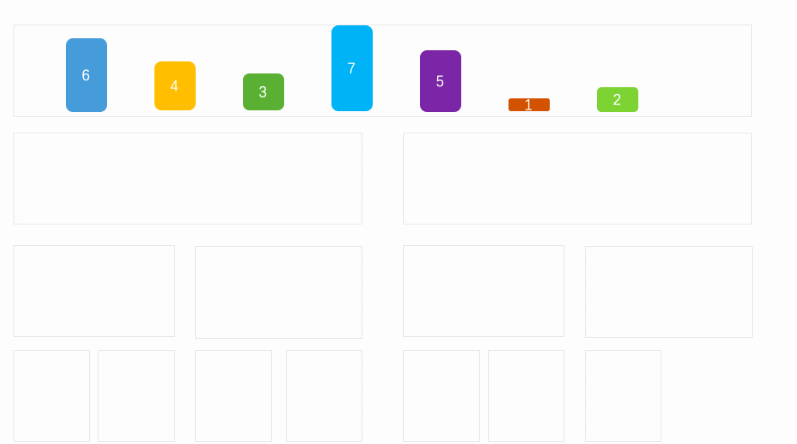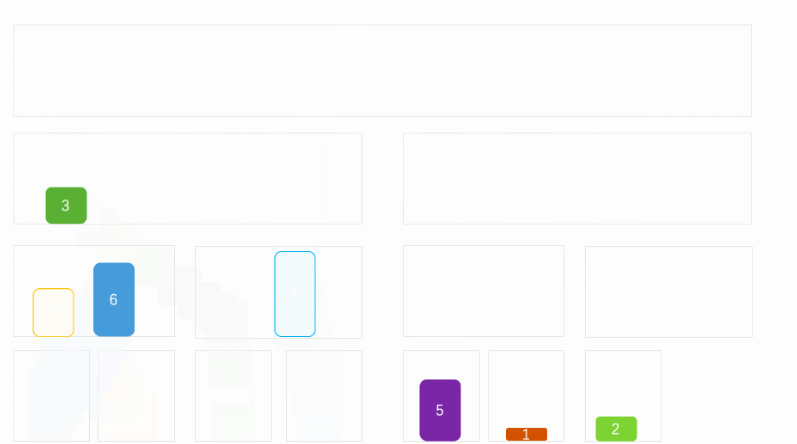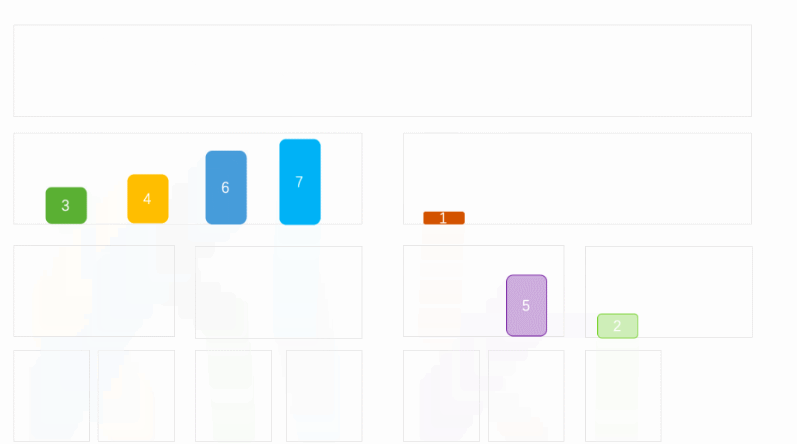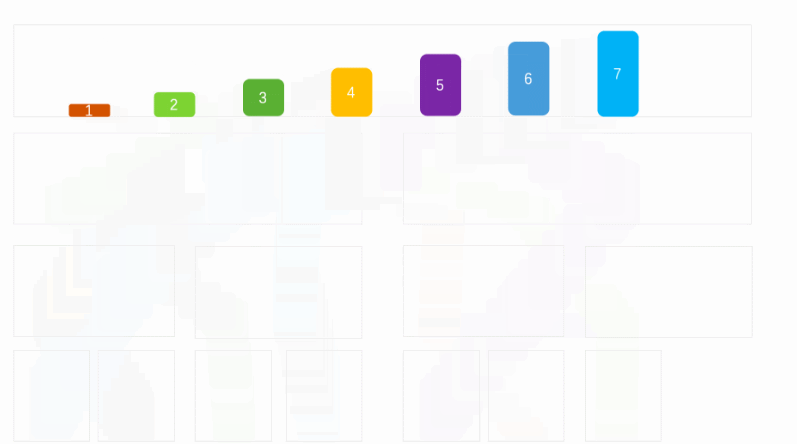
Merge sort is to divide the data in the array into two and divide the data into smaller sequence arrays in turn, Until the array cannot be further divided (the maximum number of array elements is 1). Then, add the elements in the array to the new array level by level in size order until all the elements are filled into the new array, and then pass the elements in the ordered new array to the original array to realize the sorting operation.
The code implementation is as follows.
public static void main(String []args) {
int[] a = new int[]{3, 2, 6, 1, 9, 5, 3, 6, 1, 7, 9, 2, 5};
int[] temp = new int[a.length];
mergesort(a,0,a.length-1,temp);//Sets the initial range of array decomposition
System.out.print(Arrays.toString(a));//Output array
}
public static void mergesort(int []a, int left,int right,int []temp){
if(left<right){
int mid = (left+right)/2;//Sets the median value of the array decomposition
mergesort(a,left,mid,temp);//Recursive decomposition of the first half
mergesort(a,mid+1,right,temp);//Recursive decomposition of the second half
merge(a,left,mid,right,temp);//Recursive merge array
}
}
public static void merge(int a[],int left,int mid, int right, int []temp){
int i = left;//Set the start point of the left array
int j = mid+1;//Set the start point of the right array
int t = 0;//Set element insertion coordinates
//When the array elements on both sides are not sorted out, the temporary array is inserted according to the size order of the elements on the left and right sides
while (i<=mid && j<=right){
if (a[i]<=a[j]){
temp[t] = a[i];
t++;i++;
}else{
temp[t] = a[j];
t++;j++;
}
}
//Handle elements that are singled out when array elements are odd
while (i<=mid){
temp[t] = a[i];
t++;i++;
}
while (j<=right){
temp[t] = a[j];
t++;j++;
}
t = 0;//Reset subscript
int templeft = left;
while (templeft<=right){//Replace the original array with a new array
a[templeft] = temp[t];
t++;templeft++;
}
}