Sorting algorithm

Enter an integer array and output the sorted array. Here, take "no descending sorting" as an example.
I sorted out the information for follow-up search. Beginners may have mistakes. I hope you don't mind and can point it out.

Bubble sorting

Principle: search from the array header in turn, and exchange positions if there are elements less than the current position. Marked by position. There are many cycles, many exchanges and high time complexity.

public int[] BubbleSort (int[] arr) {
        for(int i=0;i<arr.length-1;i++){
            for(int j=i;j<arr.length;j++){
                if(arr[j]<arr[i]){
                    int temp=arr[i];
                    arr[i]=arr[j];
                    arr[j]=temp;
                }
            }
        }
        return arr;
}

Select sort

Locate by index. By default, the elements before the current index are in order. Search for the smallest element after index and put it on the index.

    public int[] SelectSort (int[] arr) {
        for(int i=0;i<arr.length-1;i++){
            int min=i;
            for(int j=i+1;j<arr.length;j++){
                if(arr[j]<arr[min]){
                    min=j;
                }
            }
            int temp=arr[i];
            arr[i]=arr[min];
            arr[min]=temp;
        }
        return arr;
}

Insert sort

The current position is index. By default, the elements in front of index have been ordered. Take out the elements in index and find a suitable position to insert in the first half of the ordered part. Similar to drawing playing cards.

    public int[] InsertSort (int[] arr) {
        for(int i=1;i<arr.length;i++){
            int temp=arr[i];
            int j=i-1;
            for(;j>=0;j--){
                if(arr[j]>temp)
                    arr[j+1]=arr[j];
                else{
                    break;
                }
            }
            arr[j+1]=temp;
        }
        return arr;
}

Insert sort using dichotomy

The principle is the same as the basic insertion sort, except that the dichotomy is used to find the position forward. Efficiency has been greatly improved.

    public int[] InsertSort (int[] arr) {
        for(int i=1;i<arr.length;i++){
            int temp=arr[i];
            int low=0;
            int high=i-1;
            while(low<=high){
                int mid=(low+high)/2;
                if(arr[mid]>temp)
                    high=mid-1;
                else
                    low=mid+1;
            }//At this point, the coordinate low of the first element greater than temp is found
            for(int j=i;j>low;j--){
                arr[j]=arr[j-1];
            }
            arr[low]=temp;
        }
        return arr;
    }

Shell Sort

In essence, it is the insertion sorting of different step sizes. The step size of the last round of search must be 1 to ensure that all are sorted.
The setting of step size can be changed by yourself. Here, half of the length of the array is taken.

    public int[] MySort (int[] arr) {
        int step=arr.length/2;
        while(step>=1){
            for(int i=step;i<arr.length;i++){
                for(int j=i;j>=step;j-=step){
                    if(arr[j]<arr[j-step]){
                        int temp=arr[j-step];
                        arr[j-step]=arr[j];
                        arr[j]=temp;
                    }
                    else
                        break;
                }
            }
            step--;
        }
        return arr;
    }

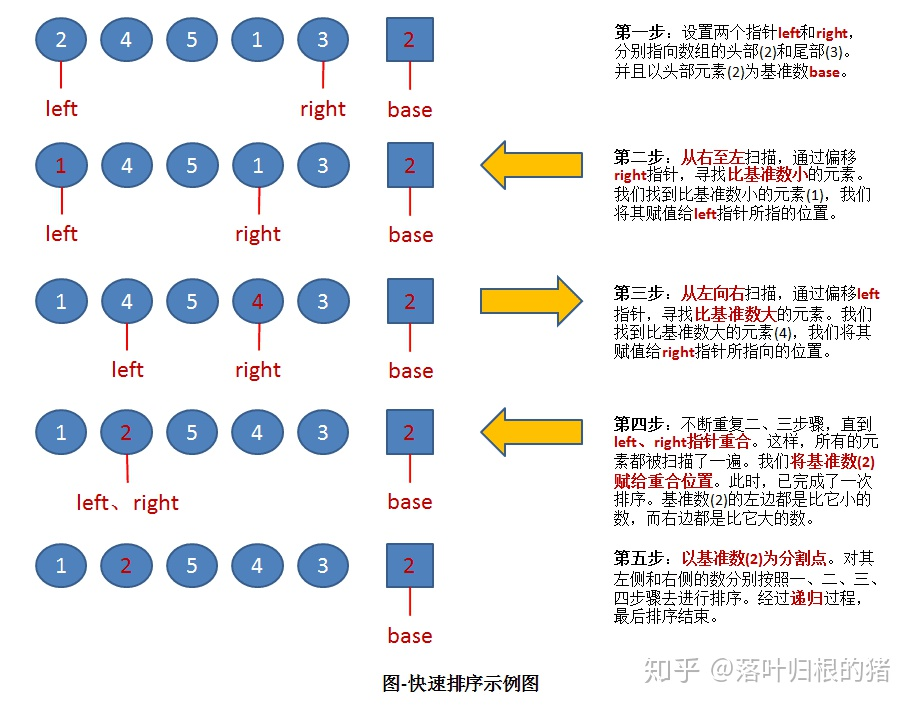
Quick sort

First find a benchmark and take this benchmark as the boundary. Those less than the benchmark are placed on the right and those greater than the benchmark are placed on the left. In this way, a sequence is divided into two, and then recursion is carried out until all the subsequences are divided.

    public int[] MySort (int[] arr) {
         quicksort(arr,0,arr.length-1);
        return arr;
    }
    private void quicksort(int[] array,int left,int right){
        if(left>=right)
            return;
        int base=array[left];
        int first=left;
        int last=right;
        while(left<right){
            for(;left<right;right--){
                if(array[right]<base){
                    array[left]=array[right];
                    break;
                }
            }
            for(;left<right;left++){
                if(array[left]>base){
                    array[right]=array[left];
                    break;
                }
            }
        }
        array[left]=base;
        quicksort(array,first,left-1);
        quicksort(array,right+1,last);
    }

Complexity: when the sequence is ordered, one of the two subsequences is empty and the other is the same as the sequence itself. At this time, the efficiency is the worst and the time complexity is the highest. When the randomness of the sequence is strong, the number of elements in the two subsequences is close to the same, and the efficiency is the highest. The average time complexity is O ( N log ⁡ N ) O(N\log N) O(NlogN).

Heap sort

Foundations: trees
The node sequence number is a complete binary tree starting from 0, and the child nodes of node i are i × 2 + 1 i\times 2+1 i × 2 + 1 and i × 2 + 2 i\times 2+2 i × 2+2 . A complete binary tree with a total of length nodes. The sequence number of the last parent node is l e n g t h / 2 − 1 length/2-1 length/2−1 .
The idea of heap sorting: build the array into a complete binary tree, and the elements of each node are greater than (less than) the elements of its child nodes. Therefore, the root node is the largest (smallest) element in the array. Output the root node elements and narrow the array range until the number of nodes is reduced to 1.
! [insert picture description here]( https://img-blog.csdnimg.cn/6c914f88568545c3a0794b23cb1dfe34.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBAd2VpeGluXzQxMDAyNzMz,size_12,color_FFFFFF,t_70,g_se,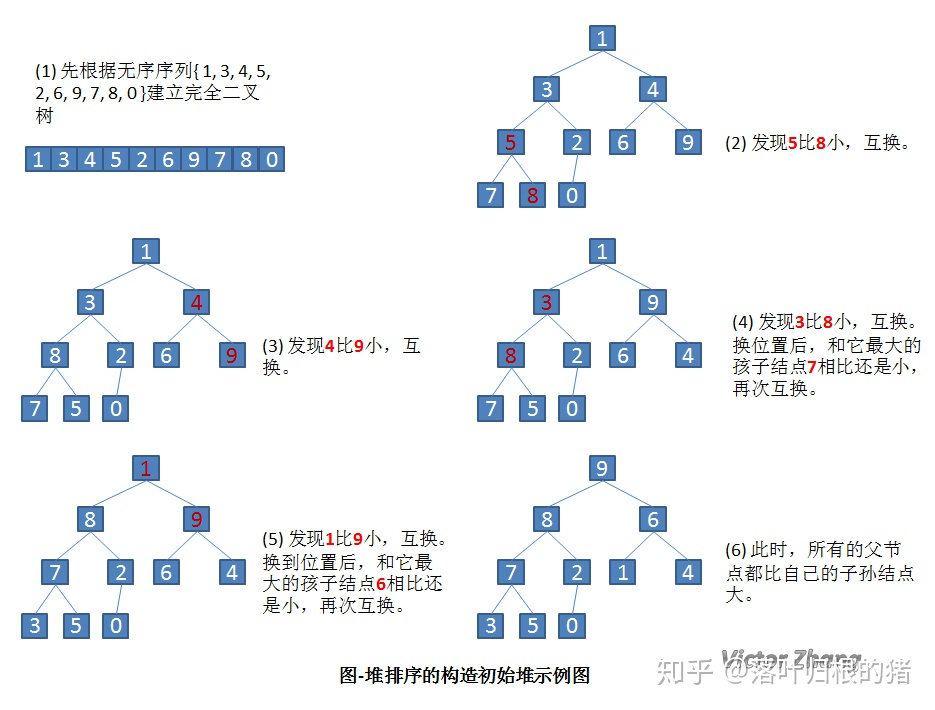

 public int[] MySort (int[] arr) {
     for(int length=arr.length;length>1;--length){
         for(int i=length/2-1;i>=0;--i){
             adjust(arr,i,length);
         }
         swap(arr,0,length-1);
     }
     return arr;
 }
    private void adjust (int[] array,int i,int length){
        int child=2*i+1;
        if(child+1<length&&array[child+1]>array[child])
            child++;
        if(array[child]>array[i]){
            swap(array,i,child);
            if(child<=length/2-1)
                adjust(array,child,length);
        }
    }
    private void swap (int[] array,int i, int j){
        int temp=array[i];
        array[i]=array[j];
        array[j]=temp;
    }

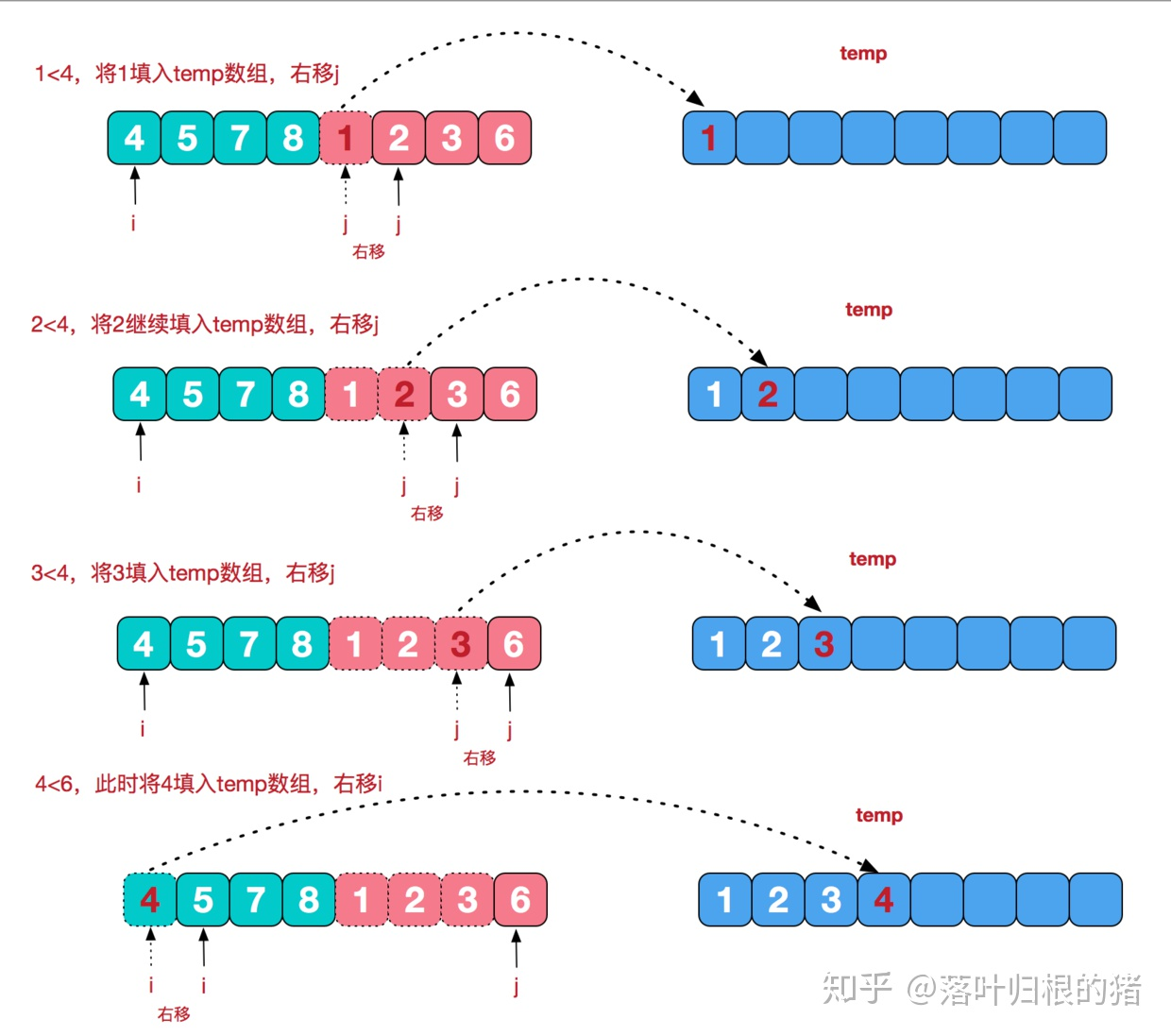
Merge sort

Split the whole sequence into half, sort them respectively, and then insert them into the new array in order. Use recursive processing.

    private int[] sort(int[] array){
        if(array.length==1){
            return array;
        }
        else
        {
            int mid=array.length/2;
            int[] temp=new int[array.length];
            int[] left=sort(Arrays.copyOfRange(array,0,mid));
            int[] right=sort(Arrays.copyOfRange(array,mid,array.length));
            int leftp=0;int rightp=0;int k=0;
            while(k<array.length){
                if(leftp<left.length&&rightp<right.length){
                    if(left[leftp]<=right[rightp]){
                        temp[k]=left[leftp];
                        leftp++;
                    }
                    else{
                        temp[k]=right[rightp];
                        rightp++;
                    }
                }
                else if(leftp>=left.length){
                    temp[k]=right[rightp];
                    rightp++;
                }
                else{
                    temp[k]=left[leftp];
                    leftp++;
                }
                k++;
            }
            return temp;
        }
    }