Follow the recipe shown below and walk through the source code.
Put together Priority Queue to summon the Dragon.
Ler's go go go!

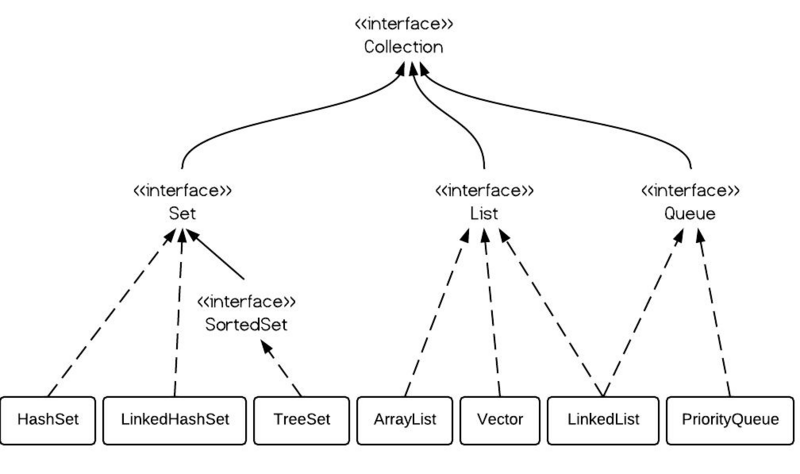
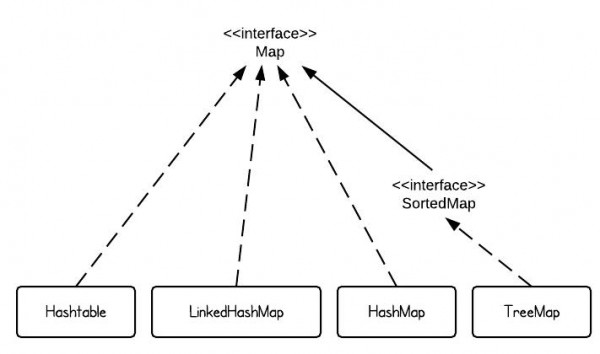
structure

/**
 * Priority queue represented as a balanced binary heap: the two
 * children of queue[n] are queue[2*n+1] and queue[2*(n+1)].  The
 * priority queue is ordered by comparator, or by the elements'
 * natural ordering, if comparator is null: For each node n in the
 * heap and each descendant d of n, n <= d.  The element with the
 * lowest value is in queue[0], assuming the queue is nonempty.
 */
transient Object[] queue; // non-private to simplify nested class access

Yes, this is an array. For a better understanding of what annotations mean, see below_.

Full binary tree:

All nodes have two leaf nodes, except the last leaf node.

The relationship between the number of nodes N and the depth d is n=2^d-1.

The number of nodes on layer I is 2^(i-1);

The parent node of the nth node: n/2, the left child node: 2n, the right child node: 2n+1; (refer to the following figure)

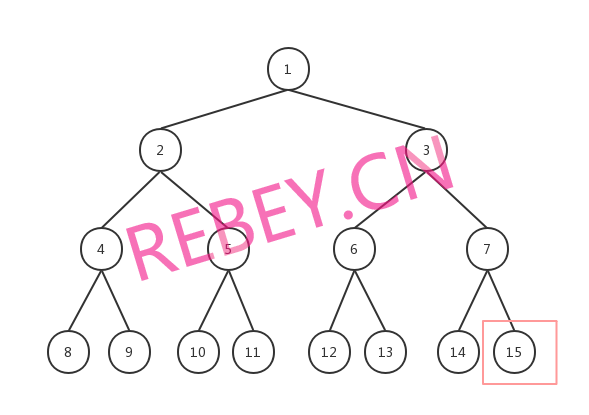
Complete binary tree:

Complete binary trees are those with and only the lowest leaf nodes that are incomplete. (For example, remove 15)

Minimum heap:

The parent node is less than the complete binary tree of the left and right child nodes.

Turn arrays:

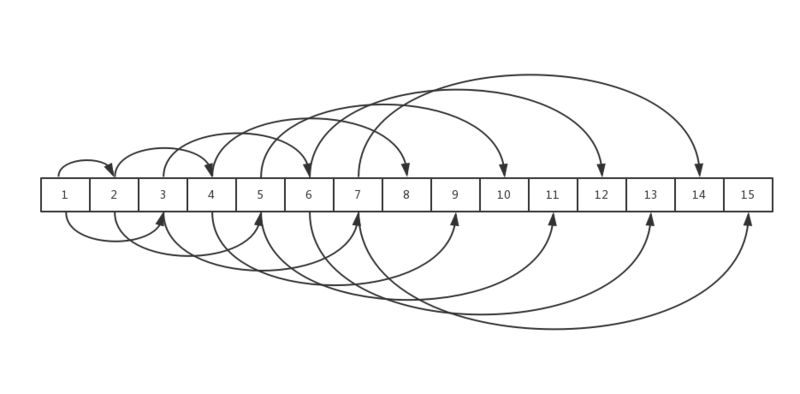
After storing the binary tree with a n array (see figure below), we can see that the root node A[0]; the left child node a[2n+1]; the right child node a[2(n+1)]; and the parent node a[(n-1)/2]. (n is an array subscript, starting at 0)

Yes, that's probably how the storage structure of the priority queue is deduced.

heapify() --> siftDown() --> siftDownComparable() --> siftDownUsingComparator()

/**
 * Establishes the heap invariant (described above) in the entire tree,
 * assuming nothing about the order of the elements prior to the call.
 */
@SuppressWarnings("unchecked")
private void heapify() {
    for (int i = (size >>> 1) - 1; i >= 0; i--)
        siftDown(i, (E) queue[i]);
}

/**
 * Inserts item x at position k, maintaining heap invariant by
 * demoting x down the tree repeatedly until it is less than or
 * equal to its children or is a leaf.
 *
 * @param k the position to fill
 * @param x the item to insert
 */
private void siftDown(int k, E x) {
    if (comparator != null)
        siftDownUsingComparator(k, x);
    else
        siftDownComparable(k, x);
}

@SuppressWarnings("unchecked")
private void siftDownComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>)x;
    int half = size >>> 1;        // loop while a non-leaf
    while (k < half) {
        int child = (k << 1) + 1; // assume left child is least
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
            c = queue[child = right];
        if (key.compareTo((E) c) <= 0)
            break;
        queue[k] = c;
        k = child;
    }
    queue[k] = key;
}

@SuppressWarnings("unchecked")
private void siftDownUsingComparator(int k, E x) {
    int half = size >>> 1;
    while (k < half) {
        int child = (k << 1) + 1; //2n + 1, where n is the subscript
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            comparator.compare((E) c, (E) queue[right]) > 0) // Find the smallest child node
            c = queue[child = right];
        if (comparator.compare(x, (E) c) <= 0) // If the parent node is small, it exits the loop, or it is replaced.
            break;
        queue[k] = c;
        k = child;
    }
    queue[k] = x;
}

This is the minimum heaping of any array. If it is a qualified minimal heap, then all the parent nodes are in the first half of the array, and through the parent node, the left and right child nodes can be obtained. So the source code is "size > > > 1" (equal to dividing by 2), only need to cycle the first half, so that all the parent nodes are larger than the left/right child nodes after the cycle. Here non-root parent nodes are compared many times. heapify() will give you the smallest heap array described above.

@SuppressWarnings("unchecked")
public E poll() {
    if (size == 0)
        return null;
    int s = --size;
    modCount++;
    E result = (E) queue[0];
    E x = (E) queue[s];
    queue[s] = null;
    if (s != 0)
        siftDown(0, x); // !
    return result;
}

The core of poll() is also siftDown, and here "siftDown(0, x);" unlike the previous "siftDown(i, (E) queue[i];" the element corresponding to subscript 0 is not originally X. That is to say, a transformation is made here: the last queue[s] is replaced by queue[0] for a new minimum heap array.

 /**
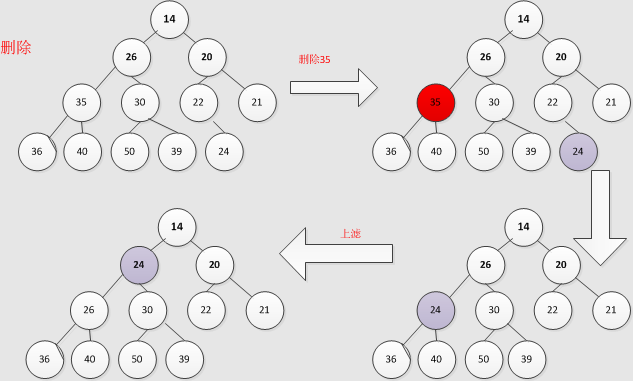
 * Removes a single instance of the specified element from this queue,
 * if it is present.  More formally, removes an element {@code e} such
 * that {@code o.equals(e)}, if this queue contains one or more such
 * elements.  Returns {@code true} if and only if this queue contained
 * the specified element (or equivalently, if this queue changed as a
 * result of the call).
 *
 * @param o element to be removed from this queue, if present
 * @return {@code true} if this queue changed as a result of the call
 */
public boolean remove(Object o) {
    int i = indexOf(o);
    if (i == -1)
        return false;
    else {
        removeAt(i);
        return true;
    }
}

/**
 * Removes the ith element from queue.
 *
 * Normally this method leaves the elements at up to i-1,
 * inclusive, untouched.  Under these circumstances, it returns
 * null.  Occasionally, in order to maintain the heap invariant,
 * it must swap a later element of the list with one earlier than
 * i.  Under these circumstances, this method returns the element
 * that was previously at the end of the list and is now at some
 * position before i. This fact is used by iterator.remove so as to
 * avoid missing traversing elements.
 */
@SuppressWarnings("unchecked")
private E removeAt(int i) {
    // assert i >= 0 && i < size;
    modCount++;
    int s = --size;
    if (s == i) // removed last element
        queue[i] = null;
    else {
        E moved = (E) queue[s];
        queue[s] = null;
        siftDown(i, moved); 
        if (queue[i] == moved) {
            siftUp(i, moved);
            if (queue[i] != moved)
                return moved;
        }
    }
    return null;
}

As you can see, remove() also uses siftDown() (along with siftUp(), which is described below). After siftDown, if queue[i]= moved, the left and right sub-nodes of queue[i] are larger than moved, which ensures that the sub-tree of I node is the smallest heap, but whether the parent node of queue[i] is smaller than moved is unknown, so siftUp is carried out. [2]

/**
 * Inserts item x at position k, maintaining heap invariant by
 * promoting x up the tree until it is greater than or equal to
 * its parent, or is the root.
 *
 * To simplify and speed up coercions and comparisons. the
 * Comparable and Comparator versions are separated into different
 * methods that are otherwise identical. (Similarly for siftDown.)
 *
 * @param k the position to fill
 * @param x the item to insert
 */
private void siftUp(int k, E x) {
    if (comparator != null)
        siftUpUsingComparator(k, x);
    else
        siftUpComparable(k, x);
}
    
@SuppressWarnings("unchecked")
private void siftUpComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
        if (key.compareTo((E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = key;
}

@SuppressWarnings("unchecked")
private void siftUpUsingComparator(int k, E x) {
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
        if (comparator.compare(x, (E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
}

In contrast, there is a method called siftUpComparable()/siftUpUsingComparator(). Called when new elements are added. The new element is placed in the position with the subscript size. Here, down and up refer to the direction of the object x to be compared. After comparison, x is assigned to the child node as down and the parent node as up. Of course, when you write, you may add a new one, traversing from top to bottom.

Say something

PriorityQueue is orderly; null is not allowed; non-thread security; (PriorityBlockingQueue thread security); what is not introduced is similar to other collection frameworks, such as expansion mechanism.

The elements in the priority queue are the elements with the highest priority (the smallest weight), and the priority is determined by comparing (Comparator or natural ordering of the elements themselves).

Remember to review often~~~

More interesting content, welcome to visit the author's website: rebey.cn

Recommended articles:

[1][Deep understanding of Java Collection Framework] Deep understanding of Java PriorityQueue;

[2]java Collection - Queue;