Grammar analysis
JavaCC generates a top-down parser that does not support left recursion and recursive descent. The advantage of this parser is that the syntax is easy to understand and easy to debug. Attributes can be passed up and down in the syntax parsing tree, and can also be called between branches. As shown in the figure:
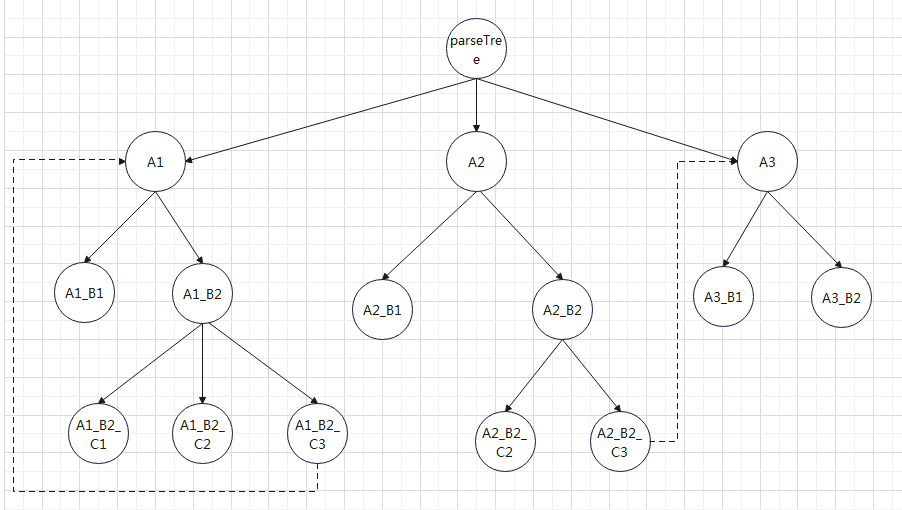
Left recursion is a kind of recursion for syntax parsing. For details, please refer to: Left recursive grammar_ Chaoer CSDN blog_ Left recursive grammar
The left recursive equivalent can be changed to the right recursive processing.
Grammar analysis is important to understand the semantics of this rule. If you understand the semantics, writing the rule is to pinch it with your hand, then the action execution will be natural.
The analytical way of four operations
//eg1: input 8+6*5-4 34//output //eg2 8+6*5-(59-3)/7 30 //eg3 -10 //input -10 //output //eg4 -10*7 //input -70 //output
We are familiar with the four operations. We can operate in the second grade of primary school. In the processing of syntax parsing, focus on solving the priority of operation: 1. Multiplication and division first; 2. Parentheses first.
Analytic tree
Before writing grammar analysis, you can draw a grammar analysis tree to sort out your ideas.
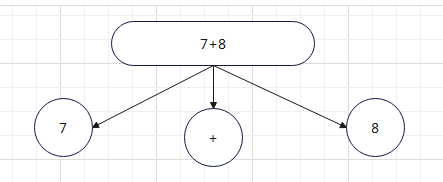
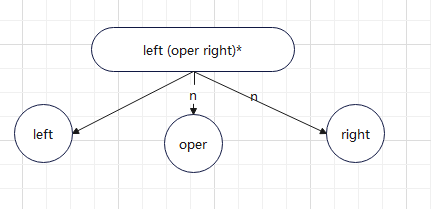
Let's start with a simple formula, 7 + 8, which can be simply parsed into a tree. But we are learning Java, and the idea of object-oriented should be necessary. We can abstract it. We can abstract "+", "-", "*", "\" into an oper symbol. The left side of the symbol is abstracted into a left object, and the right side is abstracted into a right object. Then the basic expression of the four running algorithms should be left oper right. Can't handle 7 + 8-5 yet* 6 operation formula, then use regular expression to improve it. Left (oper rignt) * means that it can handle four very long operations. Now draw the abstract parse tree, as shown in the figure:
The priority of addition, subtraction, multiplication and division has not been solved. We are analyzing the analysis of a 7 + 2 * 8 formula and draw it
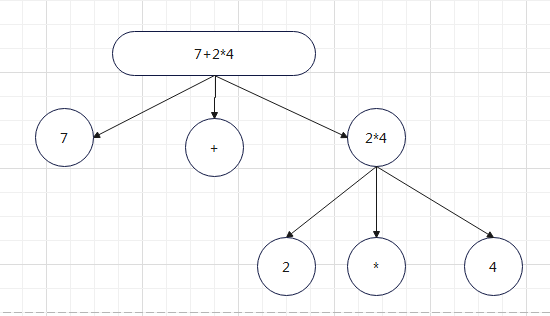
In fact, this process is to treat 2 * 4 as a subtree first, so the priority is to analyze the subtree first, calculate the data of the subtree, and then return it to the parent for operation. So let's use a little brain to improve the abstract syntax tree. As shown in the figure:
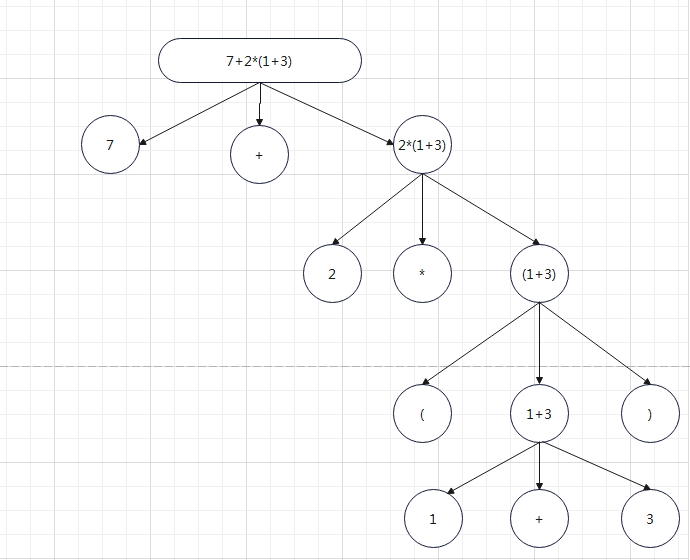
Since the priority determination of addition, subtraction, multiplication and division can be solved by constructing a subtree, the priority of "(four operations)" can also be solved by constructing a subtree. Then we will analyze the analysis of a 7 + 2 * (1 + 3) formula. As shown in the figure:
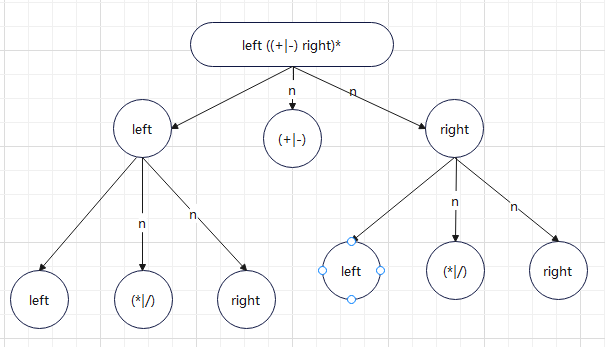
The key point is whether the four operations in "(four operations)" are consistent with the parsing process of the root node. Well, with this idea, we can upgrade the abstract syntax tree. As shown in the figure:
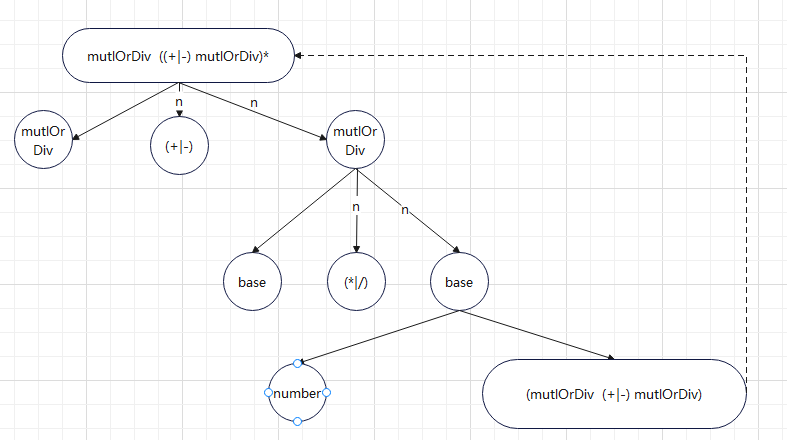
The first level tree handles addition and subtraction operations. The object of the operation is the second level tree
The secondary tree deals with multiplication and division. The object of the operation is the tertiary tree
The three-level tree handles number parsing and four operations in parentheses. The parsing of the four operations in brackets can call the root parsing.
The analysis idea of the syntax tree of these four operations is basically completed, and you can write grammar files according to the idea. In fact, grammar analysis can not be completed at one time. We need to constantly improve our ideas and try several times before it can be finalized. Drawing a grammar tree is an important way to help us clarify our thinking.
Calculator.jj
//Optional configuration parameters
options{
STATIC = false; //The generated java method is static and the default value is true
DEBUG_PARSER = true;//Enable debugging, parsing and printing. The default value is false
JDK_VERSION = "1.8";//The jdk version is used when producing java. The default version is 1.5
}
//Fixed format
PARSER_BEGIN(Calculator)
//For package name definitions like Java, the generated java file will carry this package name
package com.javacc.calculator;
//Import needs to reference java
import cn.hutool.core.date.DateUtil;
import java.io.StringReader;
public class Calculator {
//Initialization information, string receiving method and exception handling can be defined inside
public Calculator(String expr){
this(new StringReader(expr));
}
}
//Fixed format
PARSER_END(Calculator)
//Lexical definition
//SKIP is a lexical string to SKIP and ignore
SKIP : { " " | "\t" | "\n" }
TOKEN : {
<NUMBER : <DIGITS>
| <DIGITS> "." <DIGITS>
>
|
//#The beginning indicates an internal Token, which can only be used in morphology and cannot be referenced in grammar
<#DIGITS :(["0"-"9"])+>
}
TOKEN : {
< LPAREN: "(" >
| < RPAREN: ")" >
| < ADD : "+" >
| < SUBTRACT : "-" >
| < MULTIPLY : "*" >
| < DIVIDE : "/" >
}
//For debugging convenience, line feed is defined as a special token
TOKEN : { < EOL : "\n" | "\r" | "\r\n" > }
//Definition syntax
double calc():
{
double left;
double right;
}
{
left = mutlOrDiv()
(<ADD> right = mutlOrDiv() {left += right;}
| <SUBTRACT> right = mutlOrDiv() {left = left - right;}
)*
{
return left;
}
}
double mutlOrDiv():
{
double left;
double right;
}
{
left = parseBase()
(<MULTIPLY> right = parseBase() {left *= right ;}
| <DIVIDE> right = parseBase() {left = left/right;}
)*
{
return left;
}
}
double parseBase() :
{
Token t = null;
double num;
}
{
t = <NUMBER> {return Double.parseDouble(t.image);}
| <LPAREN> num = calc() <RPAREN> {return num;}
//Handle negative numbers
| <SUBTRACT> t = <NUMBER> {return 0-Double.parseDouble(t.image); }
}
The implementation idea is almost consistent with the above syntax analysis, that is, the processing of negative numbers is added to the processing of parseBase.
Test CalculatorTest class
public class CalculatorTest {
public void testCalc() throws Exception {
boolean isBeak = false;
BufferedReader reader;
String expr ="";
com.javacc.calculator.Calculator calculator ;
while (!isBeak){
System.out.println("please input four arithmetic expressions , input quit exit");
reader = new BufferedReader(new InputStreamReader(System.in));
expr = reader.readLine();
if(!"quit".equals(expr)){
calculator = new Calculator(expr);
double res = calculator.calc();
System.out.println(res);
}else {
isBeak =true;
}
}
}
public static void main(String[] args) {
CalculatorTest calculatorTest = new CalculatorTest();
try {
calculatorTest.testCalc();
} catch (Exception e) {
e.printStackTrace();
}
}
}Test 1 Effect:


Test 2 Effect:
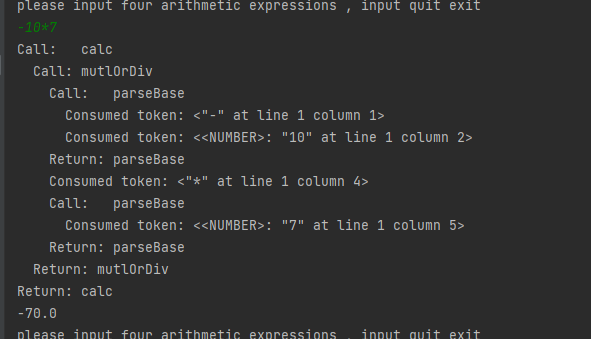
Previous: JAVACC Usage Summary (II): lexical TOKEN_IT does not code farmers blog - CSDN blog