JavaScript implements the first, middle and last order traversal of binary tree (recursive and non recursive)

1, A green binary tree

1,binary-tree.js

const binaryTree = {
    val: 'a',
    left: {
        val: 'b',
        left: {
            val: 'd',
            left: null,
            right: null
        },
        right: {
            val: 'e',
            left: null,
            right: null
        }
    },
    right: {
        val: 'c',
        left: {
            val: 'f',
            left: null,
            right: null
        },
        right: {
            val: 'g',
            left: null,
            right: null
        }
    }
}

module.exports = {
    binaryTree
}

2. Draw it

2, Recursive implementation of binary tree pre middle post order arrangement

Recursive implementation is very simple and can be completed quickly. In this era of inner volume, rounding means that everyone can write with his hands and know what he is doing

Basically, the preamble is to print at the beginning, recurse the left child, and then recurse the right child;

The middle order is to recurse the left child, print the node value, and recurse the right child;

The following sequence is recursive left child, recursive right child, and then print the node value

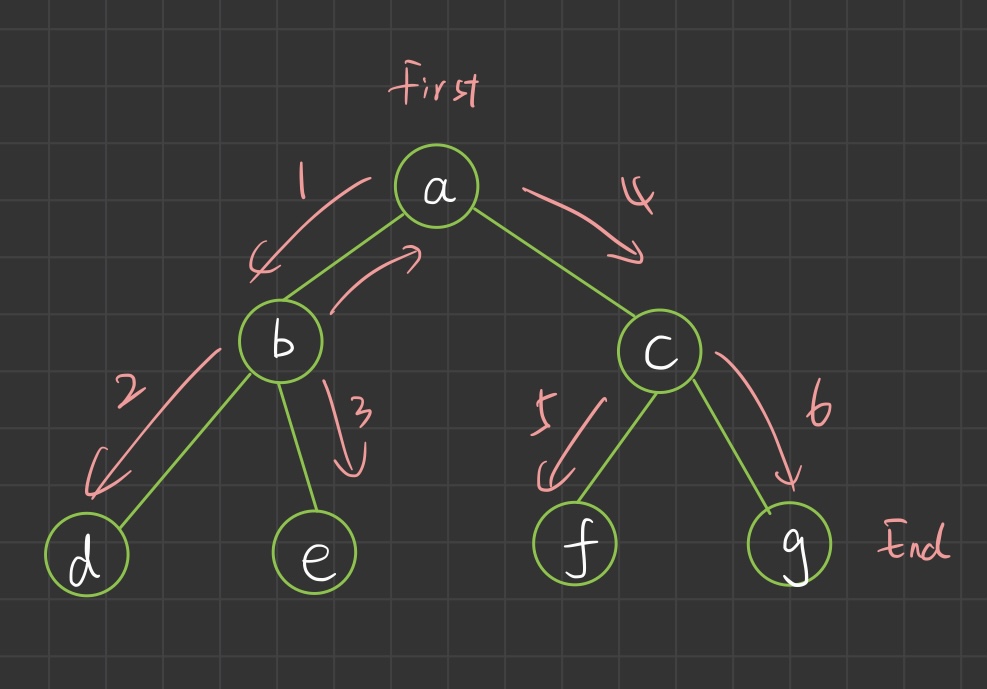
1. Preorder traversal

const { binaryTree } = require('./binary-tree')

const pre_order = root => {
    // If the node is empty, return directly
    if (!root) return;
    console.log(root.val)
    pre_order(root.left)
    pre_order(root.right)
}

pre_order(binaryTree)

// a b d e c f g

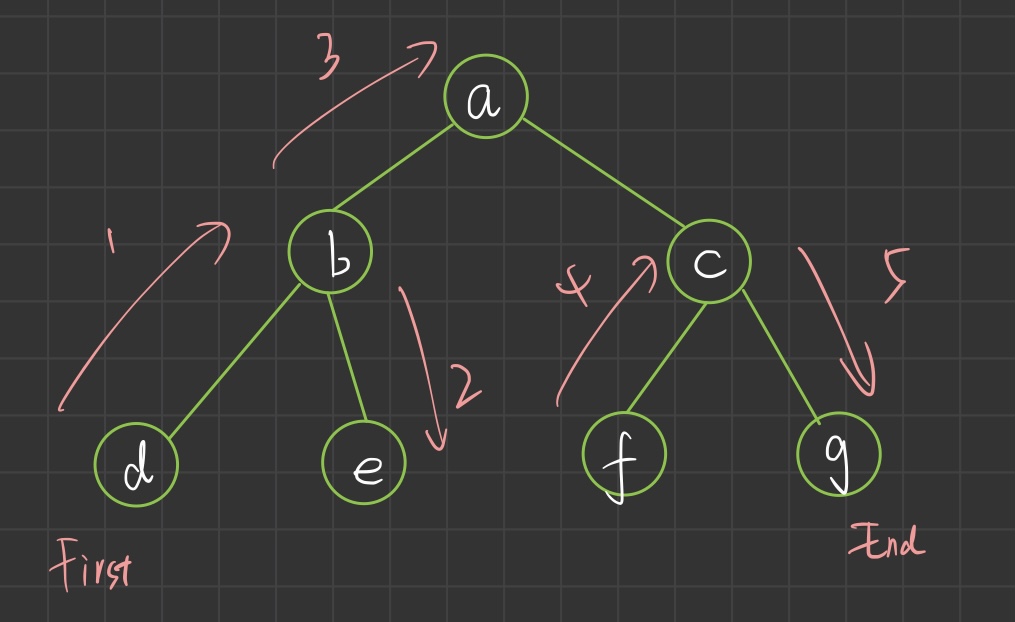
2. Medium order traversal

ctrl(command) + shift + L pre_ Change order to in_order, and then adjust the printing order

const { binaryTree } = require('./binary-tree')

const in_order = root => {
    // If the node is empty, return directly
    if (!root) return;
    in_order(root.left)
    console.log(root.val)
    in_order(root.right)
}

in_order(binaryTree)

// d b e a f c g

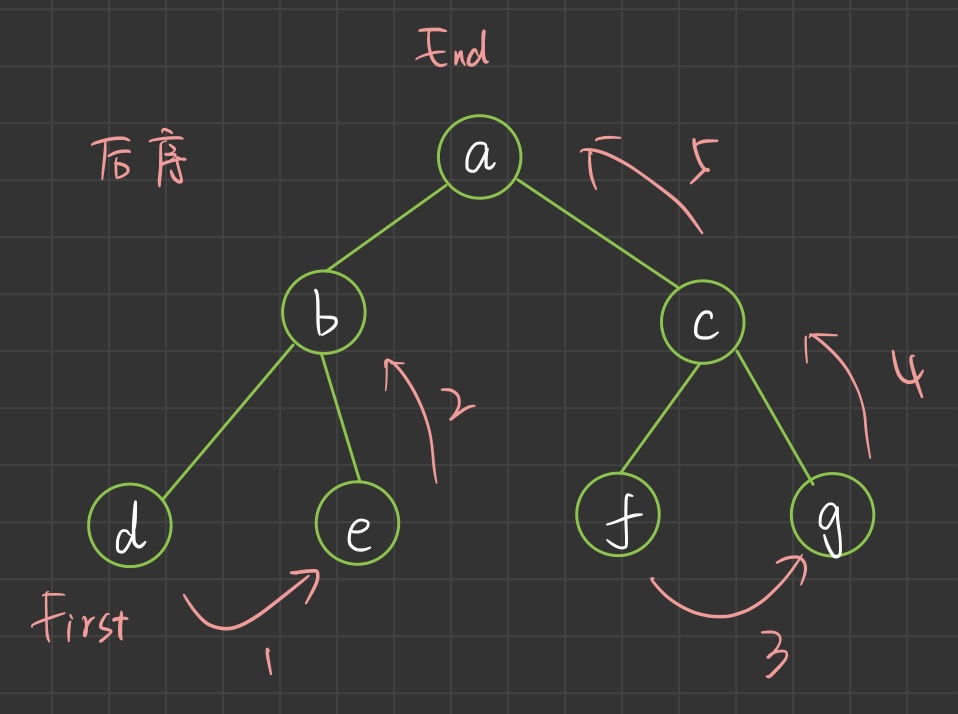
3. Postorder traversal

const { binaryTree } = require('./binary-tree')

const post_order = root => {
    // If the node is empty, return directly
    if (!root) return;
    post_order(root.left)
    post_order(root.right)
    console.log(root.val)
}

post_order(binaryTree)

// d e b f g c a

You can see with the naked eye that the implementation of recursive coding is only the order of recursion and printing. What you need to master is what the three sequential traversals mean and how they are traversed

3, Non recursive traversal of binary tree

It's a little difficult to lose~

The front, middle and back are implemented by stack

1. Non recursive preorder traversal

Look at the picture drawn earlier

const { binaryTree } = require('./binary-tree')

const nonrec_preorder = root => {
    // If the node is empty, return directly
    if (!root) return;

    const stack = [root];
    while(stack.length) {
        const node = stack.pop();
        if(node.right) stack.push(node.right);
        if(node.left) stack.push(node.left);
        console.log(node.val)
    }
}

nonrec_preorder(binaryTree)

Why push the right node first and then the left node? Because the stack is first in and last out,

In the previous recursive implementation, we already know that the result is a b d e c f g

The left node can be printed first, so the child can press the left node first, and then the child can press the right node first

The following will write post order traversal, which is the reverse of this, which can be combined

2. Order traversal in non recursive implementation

As can be seen from the recursive algorithm and diagram above, the middle order traversal will first find the leftmost child node

This can be achieved with the help of a pointer and stack

const { binaryTree } = require('./binary-tree')

const nonrec_inorder = root => {
    // If the node is empty, return directly
    if (!root) return;

    // Define a pointer to root
    let p = root;
    // Define a stack
    const stack = [];

    // This place needs to be 𞓜 p because if it is not added, it will not run in at the beginning
    while(stack.length || p) {
        // As long as p is not empty, keep looking for the left node and press the stack
        while(p) {
            stack.push(p)
            p = p.left;
        }
        // At this time in the first round, the leftmost node has been found. pop it out
        const node = stack.pop();
        console.log(node.val)
        // At this time, both the left node and the root node have pop out, and you need to traverse the right node
        p = node.right;
    }
}

nonrec_inorder(binaryTree)

3. Non recursive post order traversal

Through the careful observation of grandma

The result of postorder traversal is d e b f g c a, right

If you turn over the preorder traversal at the beginning, first "preorder traversal" from the right
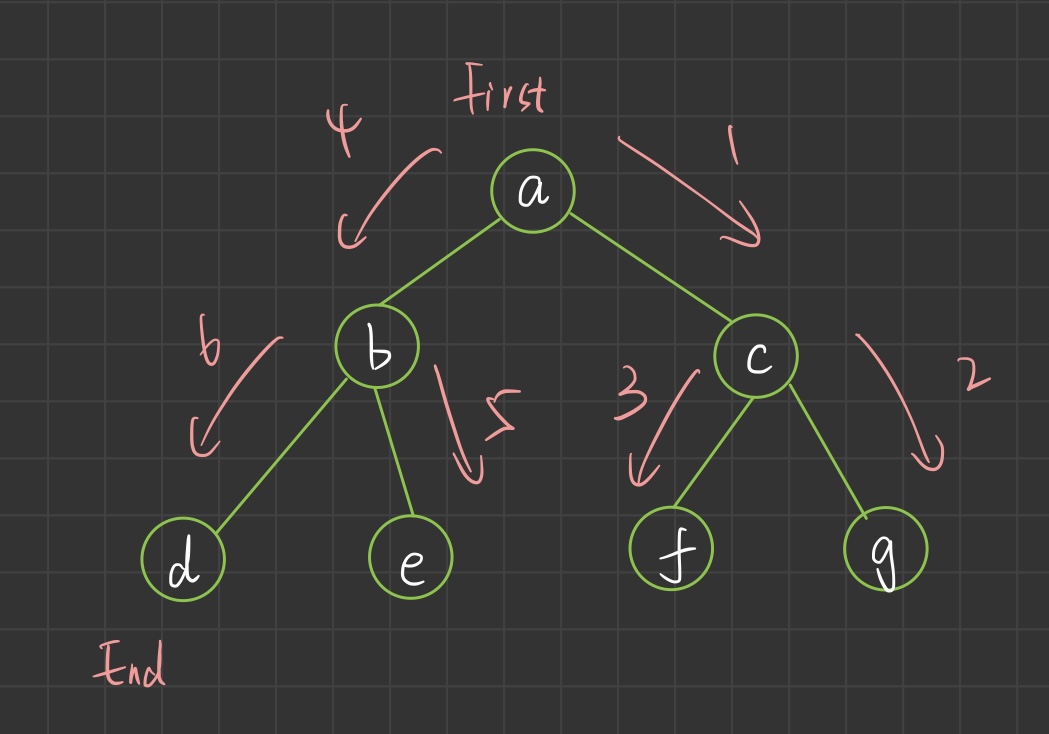This is a c g f b e d
If you read this in reverse, it's the result of post order traversal!

So according to this idea
Just turn it over and realize the "pre order traversal" from the right, and then put the result in a stack. The correct result will be output first in and then out!

const { binaryTree } = require('./binary-tree')

const nonrec_postorder = root => {
    // If the node is empty, return directly
    if (!root) return;
    // This is the same as the stack traversed by the previous sequence
    const stack = [root];
    // This is used to reverse the final result
    const out_stack = [];
    while(stack.length) {
        const node = stack.pop();
        // Collect the results of this pop every time and put them in the stack where the results are output
        out_stack.push(node);
        if(node.left) stack.push(node.left);
        if(node.right) stack.push(node.right);
    }
    // Just pop print the output stack again
    while(out_stack.length) {
        const n = out_stack.pop();
        console.log(n.val)
    }
}

nonrec_postorder(binaryTree)

All right ~ the end of the flower spreading ✿✿ヽ (° ▽ °) ノ✿ although the picture is ugly, it is painted with heart

If you like it casually, there will be one more happy, lovely and sharing woman Cheng Xuyuan on the planet~