LinkedList source code analysis
1. Introduction
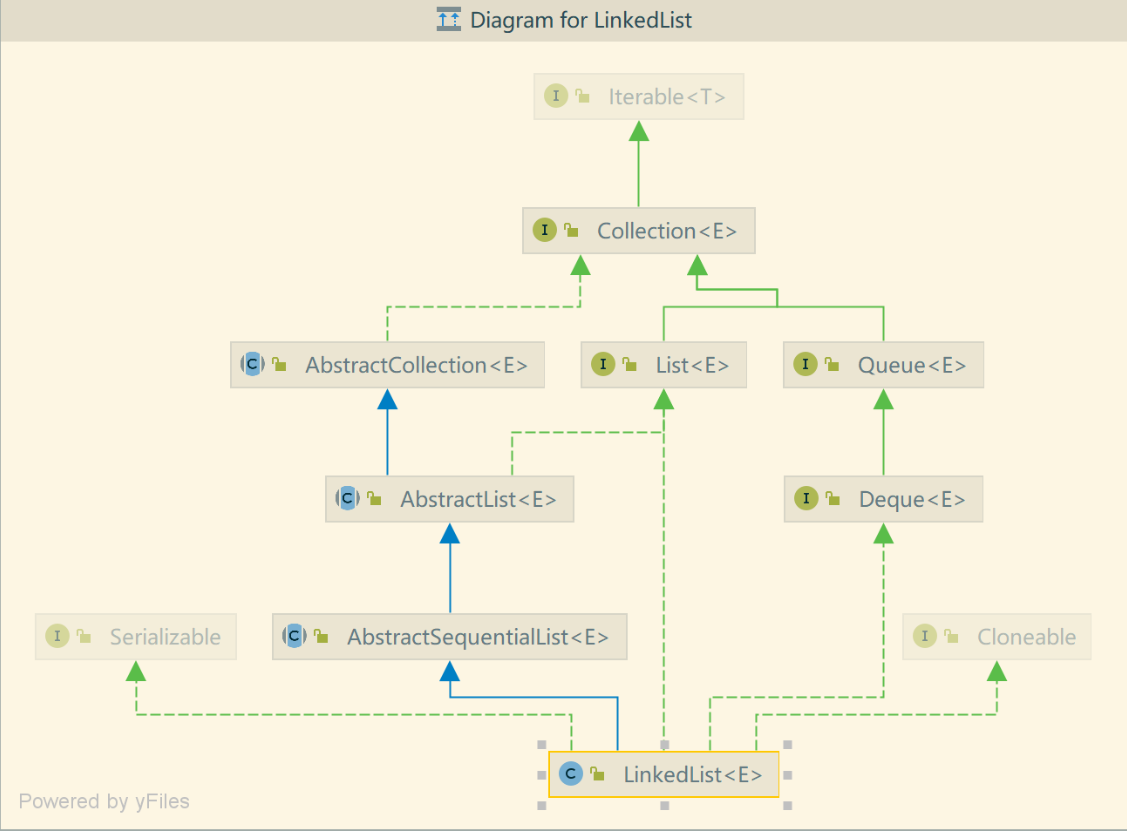
- Through the inheritance system, we can see that LinkedList not only implements the List interface, but also implements the Queue and Deque interfaces, so it can be used as a List, a double ended Queue, and of course, a stack.
- It can be seen from the inheritance system that LinkedList implements Cloneable and Serializable interfaces, indicating that it can be cloned or serialized! Similarly, when LinkedList is cloned, it is the same as ArrayList. Both are shallow copies.
2. Main attributes
// Number of elements transient int size = 0; // List head node transient Node<E> first; // End of list node transient Node<E> last;
The attribute is very simple. It defines the number of elements, size and the beginning and end nodes of the linked list. transient guarantees that it will not be serialized.
3. Main internal categories
Typical double linked list structure:
private static class Node<E> {
E item; // Elements stored by the current node
Node<E> next; // precursor
Node<E> prev; // Rear drive
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
4. Main construction methods
//Nonparametric structure
public LinkedList() {
}
//Parametric structure
public LinkedList(Collection<? extends E> c) {
this();
addAll(c);
}
5. Add elements
As a double ended queue, there are two main ways to add elements: one is to add elements at the end of the queue, and the other is to add elements at the head of the queue. These two forms are mainly realized in the LinkedList through the following two methods.
Queue header add
public void addFirst(E e) {
linkFirst(e);
}
// Add element to queue header
private void linkFirst(E e) {
// First node
final Node<E> f = first;
// Create a new node
final Node<E> newNode = new Node<>(null, e, f);
// Make the new node the first node
first = newNode;
// Determine whether it is the first element added
// If so, set last as the new node
//Otherwise, set the prev pointer of the original first node to the new node
if (f == null)
last = newNode;
else
f.prev = newNode;
// Number of elements plus one
size++;
// The number of modifications plus one indicates that this is a set that supports fail fast
modCount++;
}
Add at the end of queue
public void addLast(E e) {
linkLast(e);
}
// Add element from end of queue
void linkLast(E e) {
// Queue tail node
final Node<E> l = last;
// Create a new node. The prev of the new node is the tail node
final Node<E> newNode = new Node<>(l, e, null);
// Make the new node the new tail node
last = newNode;
// Determine whether it is the first element added
// If so, set first as the new node
// Otherwise, set the next pointer of the original node to the new node
if (l == null)
first = newNode;
else
l.next = newNode;
//Number of elements plus one
size++;
// Number of modifications plus one
modCount++;
}
As an unbounded queue, adding elements always succeeds:
public boolean offerFirst(E e) {
addFirst(e);
return true;
}
public boolean offerLast(E e) {
addLast(e);
return true;
}
As a List, you need to support adding elements in the middle, mainly through the following method.
Add at specified location
//Adds an element at the specified index location
public void add(int index, E element) {
//Check for out of bounds
checkPositionIndex(index);
//If index is a position after the end of the queue node
//Add the new node directly after the tail node
//Otherwise, the linkBefore() method is called to add nodes in the middle
if (index == size)
linkLast(element);
else
linkBefore(element, node(index));
}
//Find the node corresponding to the index location
Node<E> node(int index) {
//Because it is a double linked list, it determines whether to traverse from the front or from the back according to whether the index is in the first half or the second half
//In this way, index can traverse half the elements less
if (index < (size >> 1)) {
//If it's in the first half
//Previous traversal
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {
//In the second half if
//Just traverse from the back
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
// Add element before node succ
void linkBefore(E e, Node<E> succ) {
// Find the front node of the node to be added, that is, the front node of succ
final Node<E> pred = succ.prev;
// Create a new node between its predecessor and successor
final Node<E> newNode = new Node<>(pred, e, succ);
// Modify the leading pointer of the subsequent node to point to the new node
succ.prev = newNode;
// Judge whether the front node is empty
//If it is empty, it indicates that it is the first added element. Modify the first pointer
//Copy and modify the nxet of the front node as a new node
if (pred == null)
first = newNode;
else
pred.next = newNode;
//Number of elements + 1
size++;
//Modification times + 1
modCount++;
}
The method of adding elements in the middle of LinkedList is also very simple. A typical double linked list adds elements in the middle.
summary
The three ways to add elements are roughly as shown in the following figure:
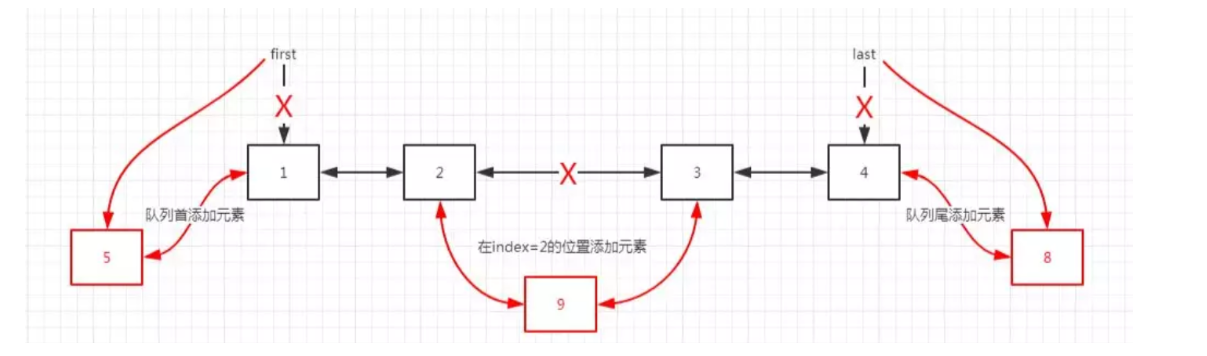
- Adding elements at the beginning and end of the queue is very efficient, and the time complexity is O(1).
- Adding elements in the middle is inefficient. First, find the node at the insertion position, and then modify the pointers of the front and rear nodes. The time complexity is O(n).
6. Delete element
As a double ended queue, there are two ways to delete elements, one is to delete elements at the beginning of the queue, and the other is to delete elements at the end of the queue.
As a List, it also supports intermediate deletion of elements, so there are three methods to delete elements, as follows:
Delete header node
//An exception is thrown if no element is remove d
public E removeFirst() {
final Node<E> f = first;
if (f == null)
throw new NoSuchElementException();
return unlinkFirst(f);
}
//poll returns null if there is no element
public E pollFirst() {
final Node<E> f = first;
return (f == null) ? null : unlinkFirst(f);
}
//Delete first node
private E unlinkFirst(Node<E> f) {
//Element value of the first node
final E element = f.item;
//next pointer of the first node
final Node<E> next = f.next;
//Set the value of the first node to null to assist the GC
f.item = null;
f.next = null; // help GC
//Take the next of the first node as the new first node
first = next;
//If only one element is deleted, set last to null
//Otherwise, set the leading pointer of next to null
if (next == null)
last = null;
else
next.prev = null;
//Number of elements minus one
size--;
//Number of modifications plus one
modCount++;
//Returns the deleted element
return element;
}
Delete tail node
//An exception is thrown if no element is remove d
public E removeLast() {
final Node<E> l = last;
if (l == null)
throw new NoSuchElementException();
return unlinkLast(l);
}
//poll returns null if there is no element
public E pollLast() {
final Node<E> l = last;
return (l == null) ? null : unlinkLast(l);
}
//Delete tail node
private E unlinkLast(Node<E> l) {
//Element value of tail node
final E element = l.item;
//Leading pointer of tail node
final Node<E> prev = l.prev;
//Clear the contents of the tail node to assist the GC
l.item = null;
l.prev = null; // help GC
//Let the front node be called the new tail node
last = prev;
//If there is only one element, delete and set first to null
//Otherwise, set the next of the preceding node to null
if (prev == null)
first = null;
else
prev.next = null;
//Number of elements minus one
size--;
//Number of modifications plus one
modCount++;
//Returns the deleted element
return element;
}
Delete intermediate specified node
//Delete intermediate node
public E remove(int index) {
//Check for out of bounds
checkElementIndex(index);
//Delete the node at the specified index location
return unlink(node(index));
}
//Delete specified node
E unlink(Node<E> x) {
// Element value of node x
final E element = x.item;
// Front node of x
final Node<E> next = x.next;
// Post node of x
final Node<E> prev = x.prev;
//If the front node is empty
//The description is the first node. Let first point to the post node of x
//Otherwise, modify the post node whose next of the front node is x
if (prev == null) {
first = next;
} else {
prev.next = next;
x.prev = null;
}
//If the post node is empty
//The description is the tail node. Let last point to the front node of x
//Otherwise, modify the front node whose prev is x
if (next == null) {
last = prev;
} else {
next.prev = prev;
x.next = null;
}
//Clear the element value of x to assist GC
x.item = null;
//Number of elements minus one
size--;
//Number of modifications plus one
modCount++;
//Returns the deleted element
return element;
}
summary
The three methods of deleting elements are typical double linked list methods. The general process is shown in the following figure:
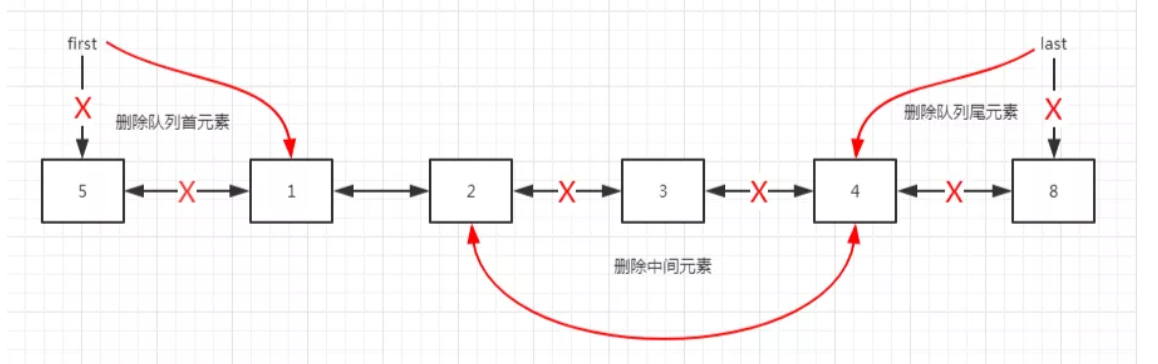
- It is efficient to delete elements at the beginning and end of the queue, and the time complexity is O(1).
- It is inefficient to delete elements in the middle. First, find the node at the deletion position, and then modify the front and rear pointers. The time complexity is O(n).
7. Removal method
Clear all elements
public void clear() {
//In order to make GC recycle the placed elements faster, you need to empty the reference relationship between node s.
for (Node<E> x = first; x != null; ) {
Node<E> next = x.next;
x.item = null;
x.next = null;
x.prev = null;
x = next;
}
first = last = null;
//Set the number of elements to 0
size = 0;
//Number of modifications plus one
modCount++;
}
8. As a stack
LinkedList is a double ended queue, which can be used as a stack.
//Element stack
public void push(E e) {
// The head element of the queue is the top element of the stack
addFirst(e);
}
//Delete the stack top element and return
public E pop() {
// The head element of the queue is the top element of the stack
return removeFirst();
}
The feature of the stack is LIFO, so it is easy to use as a stack. Adding and deleting elements only operate on the first node of the queue.
9. Summary
- LinkedList is a List implemented as a double linked List
- LinkedList is also a double ended queue, which has the characteristics of queue, double ended queue and stack
- LinkedList is very efficient in adding and deleting elements at the beginning and end of the queue, and the time complexity is O(1)
- LinkedList is inefficient to add and delete elements in the middle, and the time complexity is O(n)
- LinkedList does not support random access, so it is inefficient to access non queue elements
- LinkedList is functionally equal to ArrayList + ArrayDeque
