1, Introduction
HashMap is implemented by hash table, with key/value storage structure. Each key corresponds to a unique value. The speed of query and modification is very fast, and can reach the average time complexity of O(1). It is non thread safe and does not guarantee the storage order of elements;
2, Inheritance class diagram

1. hashMap implements Cloneable, which means cloning can be performed
2. hashMap implements Serializable, which means it can be serialized
3. hashMap inherits AbstractMap and implements the Map interface.

3, Data structure

The implementation of HashMap adopts the structure of [array + linked list + red black tree]. When the number of elements in the linked list reaches 8, it will be transformed into red black tree to improve the query efficiency

4, Source code analysis

1. Member properties

Here we can see some key attributes, such as:
The default initial capacity is 16
The loading factor is 0.75 (the loading factor is used to calculate the capacity expansion when the capacity reaches)
Treelization: when the length of the linked list reaches 8 and the array length reaches 64, treelization is carried out. When the length of the linked list is less than 6, treelization is reversed

/**
 * The default initial capacity is 16
 */
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;

/**
 * The maximum capacity is 2 to the 30th power
 */
static final int MAXIMUM_CAPACITY = 1 << 30;

/**
 * Default load factor
 */
static final float DEFAULT_LOAD_FACTOR = 0.75f;

/**
 * Tree when the number of elements in a bucket is greater than or equal to 8
 */
static final int TREEIFY_THRESHOLD = 8;

/**
 * When the number of elements in a bucket is less than or equal to 6, the tree is transformed into a linked list
 */
static final int UNTREEIFY_THRESHOLD = 6;

/**
 * Only when the number of buckets reaches 64 can the tree be formed
 */
static final int MIN_TREEIFY_CAPACITY = 64;

/**
 * Array, also known as bucket
 */
transient Node<K,V>[] table;

/**
 * Cache as entrySet()
 */
transient Set<Map.Entry<K,V>> entrySet;

/**
 * Number of elements
 */
transient int size;

/**
 * Modification times, which is used to implement the quick failure strategy during iteration
 */
transient int modCount;

/**
 * Expand the capacity when the number of buckets reaches, threshold = capacity * loadFactor
 */
int threshold;

/**
 * Loading factor
 */
final float loadFactor;

1. Constructor

HashMap() construction method

The parameterless constructor simply assigns the default load factor

   public HashMap() {
        this.loadFactor = DEFAULT_LOAD_FACTOR; // all other fields defaulted
    }

HashMap(int initialCapacity) construction method

Here, the HashMap(int initialCapacity, float loadFactor) construction method is called and the default load factor is passed in.

public HashMap(int initialCapacity) {
    this(initialCapacity, DEFAULT_LOAD_FACTOR);
}

HashMap(int initialCapacity) construction method

Here, first check whether the incoming capacity and load factor are legal, and then calculate the capacity expansion threshold according to the capacity. Threshold is calculated as the incoming initial capacity, taking the nearest n-th power of 2

public HashMap(int initialCapacity, float loadFactor) {
    // Check whether the incoming initial capacity is legal
    if (initialCapacity < 0)
        throw new IllegalArgumentException("Illegal initial capacity: " +
                                           initialCapacity);
    if (initialCapacity > MAXIMUM_CAPACITY)
        initialCapacity = MAXIMUM_CAPACITY;
    // Check whether the loading factor is legal
    if (loadFactor <= 0 || Float.isNaN(loadFactor))
        throw new IllegalArgumentException("Illegal load factor: " +
                                           loadFactor);
    this.loadFactor = loadFactor;
    // Calculate expansion threshold
    this.threshold = tableSizeFor(initialCapacity);
}

static final int tableSizeFor(int cap) {
    // The expansion threshold is the incoming initial capacity, which is taken up to the nearest n-th power of 2
    int n = cap - 1;
    n |= n >>> 1;
    n |= n >>> 2;
    n |= n >>> 4;
    n |= n >>> 8;
    n |= n >>> 16;
    return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}

1. Member method
   put(K key, V value) method - > store element

(1) First, a hash value is calculated according to the key, and then the corresponding bucket is determined according to the hash value

(2) If the number of buckets is 0, initialize the hash table [lazy loading] first

(3) If the bucket corresponding to the key has no elements, it can be directly placed in the first position of the bucket

(4) If the same key exists in the bucket, it indicates that it already exists before, then replace it. Save the new value here and replace it in step 9

(5) If the first element is a tree node, call putTreeVal() of the tree node to find the element or insert the tree node;

(6) If not, traverse the linked list corresponding to the bucket to find out whether the key exists in the linked list;

(7) If the corresponding process element (key) is found, it will be transferred to the following process (9);

(8) If the element corresponding to the key is not found, insert a new node at the end of the linked list and judge whether it needs to be trealized;

(9) If the element corresponding to the key is found, judge whether to replace the old value and directly return the old value;

(10) If an element is inserted, add 1 to the quantity and judge whether it needs to be expanded;

public V put(K key, V value) {
    // Call hash(key) to calculate the hash value of the key
    return putVal(hash(key), key, value, false, true);
}

static final int hash(Object key) {
    int h;
    // If the key is null, the hash value is 0. Otherwise, call the hashCode() method of the key
    // And make the upper 16 bits exclusive or with the whole hash. This is to make the calculated hash more dispersed
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    Node<K, V>[] tab;
    Node<K, V> p;
    int n, i;
    // Initialize if the number of buckets is 0
    if ((tab = table) == null || (n = tab.length) == 0)
        // Call resize() to initialize
        n = (tab = resize()).length;
    // (n - 1) & hash calculates which bucket the element is in
    // If there is no element in the bucket, put the element in the first position in the bucket
    if ((p = tab[i = (n - 1) & hash]) == null)
        // Create a new node and put it in the bucket
        tab[i] = newNode(hash, key, value, null);
    else {
        // If an element already exists in the bucket
        Node<K, V> e;
        K k;
        // If the key of the first element in the bucket is the same as that of the element to be inserted, save it to e for subsequent modification of the value value
        if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
        else if (p instanceof TreeNode)
            // If the first element is a tree node, the putTreeVal of the tree node is called to insert the element
            e = ((TreeNode<K, V>) p).putTreeVal(this, tab, hash, key, value);
        else {
            // Traverse the linked list corresponding to this bucket, and binCount is used to store the number of elements in the linked list
            for (int binCount = 0; ; ++binCount) {
                // After traversing, no new key is found in the linked list. If no new key is found in the linked list, it indicates that the last key does not exist
                if ((e = p.next) == null) {
                    p.next = newNode(hash, key, value, null);
                    // If the length of the linked list after inserting a new node is greater than 8, judge whether it needs to be trealized. Because the first element is not added to binCount, here - 1
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash);
                    break;
                }
                // If the key to be inserted is found in the linked list, exit the loop
                if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }
        // If the element corresponding to the key is found
        if (e != null) { // existing mapping for key
            // Record the old value
            V oldValue = e.value;
            // Determine whether the old value needs to be replaced
            if (!onlyIfAbsent || oldValue == null)
                // Replace old value with new value
                e.value = value;
            // Do something after the node is accessed, which is used in LinkedHashMap
            afterNodeAccess(e);
            // Return old value
            return oldValue;
        }
    }
    // That's it. No element found
    // Number of modifications plus 1
    ++modCount;
    // Add 1 to the number of elements to determine whether capacity expansion is required
    if (++size > threshold)
        // Capacity expansion
        resize();
    // Do something after the node is inserted, which is used in LinkedHashMap
    afterNodeInsertion(evict);
    // Element not found returned null
    return null;
}

resize() method - > capacity expansion method
(1) Check that if the old capacity reaches the maximum, the capacity will not be expanded

(2) If the old capacity is greater than 0, the new capacity is equal to 2 times of the old capacity, but does not exceed the 30th power of the maximum capacity 2, and the new capacity expansion threshold is 2 times of the old capacity expansion threshold;

(3) If the default construction method is used, it will be initialized to the default value when the element is inserted for the first time, with a capacity of 16 and a capacity expansion threshold of 12;

(4) If the non default construction method is used, the initialization capacity is equal to the expansion threshold when the element is inserted for the first time, and the expansion threshold is equal to the nth power of the nearest 2 of the incoming capacity in the construction method;

(5) Create a new capacity bucket;

(6) Move the element. The original element hash es the capacity of the new array. The original linked list is divided into two linked lists. The low-level linked list is stored in the position of the original bucket, and the high-level linked list is moved to the position of the original bucket plus the old capacity;

final Node<K, V>[] resize() {
    // Old array
    Node<K, V>[] oldTab = table;
    // Old capacity
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    // Old capacity expansion threshold
    int oldThr = threshold;
    int newCap, newThr = 0;
    if (oldCap > 0) {
        if (oldCap >= MAXIMUM_CAPACITY) {
            // If the old capacity reaches the maximum capacity, it will not be expanded
            threshold = Integer.MAX_VALUE;
            return oldTab;
        } else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                oldCap >= DEFAULT_INITIAL_CAPACITY)
            // If twice the old capacity is less than the maximum capacity and the old capacity is greater than the default initial capacity (16), the capacity is expanded to two and the expansion threshold is also expanded to twice
            newThr = oldThr << 1; // double threshold
    } else if (oldThr > 0) // initial capacity was placed in threshold
        // For a map created using a non default construction method, this is where the first element is inserted
        // If the old capacity is 0 and the old capacity expansion threshold is greater than 0, assign the new capacity to the old threshold
        newCap = oldThr;
    else {               // zero initial threshold signifies using defaults
        // The map created by calling the default construction method will come here for the first time
        // If both the old capacity and the old capacity expansion threshold are 0, it indicates that they have not been initialized, then the initialization capacity is the default capacity, and the capacity expansion threshold is the default capacity * default loading factor
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int) (DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    if (newThr == 0) {
        // If the new capacity expansion threshold is 0, it is calculated as capacity * loading factor, but it cannot exceed the maximum capacity
        float ft = (float) newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float) MAXIMUM_CAPACITY ?
                (int) ft : Integer.MAX_VALUE);
    }
    // Assign the expansion threshold as the new threshold
    threshold = newThr;
    // Create a new capacity array
    @SuppressWarnings({"rawtypes", "unchecked"})
    Node<K, V>[] newTab = (Node<K, V>[]) new Node[newCap];
    // Assign bucket to new array
    table = newTab;
    // If the old array is not empty, move the element
    if (oldTab != null) {
        // Traverse old array
        for (int j = 0; j < oldCap; ++j) {
            Node<K, V> e;
            // If the first element in the bucket is not empty, it is assigned to e
            if ((e = oldTab[j]) != null) {
                // Empty the old bucket for GC recycling  
                oldTab[j] = null;
                // If there is only one element in this bucket, calculate its position in the new bucket and move it to the new bucket
                // Because the capacity is expanded twice every time, there must be no element in the new bucket when the first element here is moved to the new bucket
                if (e.next == null)
                    newTab[e.hash & (newCap - 1)] = e;
                else if (e instanceof TreeNode)
                    // If the first element is a tree node, break up the tree into two trees and insert them into a new bucket
                    ((TreeNode<K, V>) e).split(this, newTab, j, oldCap);
                else { // preserve order
                    // If the linked list has more than one element and is not a tree
                    // Then it is divided into two linked lists and inserted into a new bucket
                    // For example, if the original capacity is 4, 3, 7, 11 and 15, these four elements are all in bucket 3
                    // Now when the capacity is expanded to 8, 3 and 11 are still in barrel 3, and 7 and 15 will be moved to barrel 7
                    // That is, it is divided into two linked lists
                    Node<K, V> loHead = null, loTail = null;
                    Node<K, V> hiHead = null, hiTail = null;
                    Node<K, V> next;
                    do {
                        next = e.next;
                        // (e.hash & oldcap) = = 0 elements are placed in the low linked list
                        // For example, 3 & 4 = = 0
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        } else {
                            // (e.hash & oldCap) !=  The element of 0 is placed in the high-order linked list
                            // For example, 7 & 4= 0
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    // After traversal, it is divided into two linked lists
                    // The position of the low-level linked list in the new bucket is the same as that in the old bucket (i.e. 3 and 11 are still in bucket 3)
                    if (loTail != null) {
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    // The position of the high-level linked list in the new bucket is exactly the original position plus the old capacity (that is, 7 and 15 have been moved to bucket 7)
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}

TreeNode. putTreeVal(...) -> The method of inserting elements into the red black tree.

(1) Start traversing from the root node of the red black tree, and compare according to the balance characteristics of the val tree

(2) Compare the hash value and key value. If they are the same, return directly and decide whether to replace the value value in the putVal() method;

(3) Determine whether to search in the left or right subtree of the tree according to the hash value and key value, and return directly when it is found;

(4) If it is not found at last, insert elements in the corresponding position of the tree and balance them;

final TreeNode<K, V> putTreeVal(HashMap<K, V> map, Node<K, V>[] tab,
                                int h, K k, V v) {
    Class<?> kc = null;
    // Mark whether the node of this key is found
    boolean searched = false;
    // Find the root node of the tree
    TreeNode<K, V> root = (parent != null) ? root() : this;
    // Start traversing from the root node of the tree
    for (TreeNode<K, V> p = root; ; ) {
        // dir=direction, is the mark on the left or right
        // ph=p.hash, the hash value of the current node
        int dir, ph;
        // pk=p.key, the key value of the current node
        K pk;
        if ((ph = p.hash) > h) {
            // The current hash is larger than the target hash. The description is on the left
            dir = -1;
        }
        else if (ph < h)
            // The current hash is smaller than the target hash. The description is on the right
            dir = 1;
        else if ((pk = p.key) == k || (k != null && k.equals(pk)))
            // If the two hash es are the same and the key s are the same, it means that the node is found and returned directly
            // Go back to putVal() to determine whether to modify its value value
            return p;
        else if ((kc == null &&
                // If k is a subclass of Comparable, return its real class; otherwise, return null
                (kc = comparableClassFor(k)) == null) ||
                // If k and pk are not of the same type, return 0; otherwise, return the result of comparison between them
                (dir = compareComparables(kc, k, pk)) == 0) {
            // This condition indicates that the two hash es are the same, but one of them is not of Comparable type or the two types are different
            // For example, if the key is of Object type, you can pass String or Integer. The hash values of the two may be the same
            // Storing elements with the same hash value in the same subtree in the red black tree is equivalent to finding the vertex of the subtree
            // Traverse the left and right subtrees respectively from this vertex to find whether there are the same elements as the key to be inserted
            if (!searched) {
                TreeNode<K, V> q, ch;
                searched = true;
                // Traverse the left and right subtrees and find the direct return
                if (((ch = p.left) != null &&
                        (q = ch.find(h, k, kc)) != null) ||
                        ((ch = p.right) != null &&
                                (q = ch.find(h, k, kc)) != null))
                    return q;
            }
            // If the two types are the same, calculate the hash value according to their memory address for comparison
            dir = tieBreakOrder(k, pk);
        }

        TreeNode<K, V> xp = p;
        if ((p = (dir <= 0) ? p.left : p.right) == null) {
            // If the element corresponding to the key is not found in the end, a new node will be created
            Node<K, V> xpn = xp.next;
            TreeNode<K, V> x = map.newTreeNode(h, k, v, xpn);
            if (dir <= 0)
                xp.left = x;
            else
                xp.right = x;
            xp.next = x;
            x.parent = x.prev = xp;
            if (xpn != null)
                ((TreeNode<K, V>) xpn).prev = x;
            // Balance after inserting tree nodes
            // Move the root node to the first node in the linked list
            moveRootToFront(tab, balanceInsertion(root, x));
            return null;
        }
    }
}

treeifyBin() method

If the length of the linked list after inserting elements is greater than or equal to 8, judge whether it needs to be treelized.

(1) It can be found here that the capacity expansion is not carried out immediately when the length of the linked list is greater than 8. He will first check whether the length of the array is less than 64. If it is less than 64, the capacity expansion will be carried out, because after the capacity expansion, it can play the role of rehash and scatter the linked list elements of the previous bucket into two buckets. In this way, the capacity expansion can not be solved in the extreme case, so the tree may be carried out next time.

(1) If the array length is greater than 64, all nodes will be constructed into tree nodes, and then the tree will be started

final void treeifyBin(Node<K, V>[] tab, int hash) {
    int n, index;
    Node<K, V> e;
    if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
        // If the number of barrels is less than 64, expand the capacity directly without tree
        // Because after capacity expansion, the linked list will be divided into two linked lists to reduce elements
        // Of course, not necessarily. For example, if the capacity is 4, all the elements stored in it are divided by 4 and the remainder is equal to 3
        // In this way, even if the capacity is expanded, the length of the linked list cannot be reduced
        resize();
    else if ((e = tab[index = (n - 1) & hash]) != null) {
        TreeNode<K, V> hd = null, tl = null;
        // Replace all nodes with tree nodes
        do {
            TreeNode<K, V> p = replacementTreeNode(e, null);
            if (tl == null)
                hd = p;
            else {
                p.prev = tl;
                tl.next = p;
            }
            tl = p;
        } while ((e = e.next) != null);
        // If you have entered the above cycle, start the tree from the beginning
        if ((tab[index] = hd) != null)
            hd.treeify(tab);
    }
}

TreeNode.treeify() method. - > Tree method

(1) The traversal starts from the first element of the linked list, and the first element is used as the root node

(2) Other elements are inserted into the red black tree in turn, and then balanced;

(3) Move the root node to the position of the first element of the linked list (because the root node will change when balancing);

final void treeify(Node<K, V>[] tab) {
    TreeNode<K, V> root = null;
    for (TreeNode<K, V> x = this, next; x != null; x = next) {
        next = (TreeNode<K, V>) x.next;
        x.left = x.right = null;
        // The first element acts as the root node and is a black node. Other elements are inserted into the tree in turn and then balanced
        if (root == null) {
            x.parent = null;
            x.red = false;
            root = x;
        } else {
            K k = x.key;
            int h = x.hash;
            Class<?> kc = null;
            // Find the location where the element is inserted from the root node
            for (TreeNode<K, V> p = root; ; ) {
                int dir, ph;
                K pk = p.key;
                if ((ph = p.hash) > h)
                    dir = -1;
                else if (ph < h)
                    dir = 1;
                else if ((kc == null &&
                        (kc = comparableClassFor(k)) == null) ||
                        (dir = compareComparables(kc, k, pk)) == 0)
                    dir = tieBreakOrder(k, pk);

                // If the element is not found at last, it is inserted
                TreeNode<K, V> xp = p;
                if ((p = (dir <= 0) ? p.left : p.right) == null) {
                    x.parent = xp;
                    if (dir <= 0)
                        xp.left = x;
                    else
                        xp.right = x;
                    // Balance after insertion. The red node is inserted by default in the balanceInsertion() method
                    root = balanceInsertion(root, x);
                    break;
                }
            }
        }
    }
    // Move the root node to the head node of the linked list, because after balancing, the original first element is not necessarily the root node
    moveRootToFront(tab, root);
}

get(Object key) method - > get element according to key
(1) Calculate the hash value corresponding to the key and locate it to the corresponding bucket

(2) If the key of the first element is equal to the key to be found, it will be returned directly;

(3) If the first element is a tree node, look it up in the way of tree, otherwise look it up in the way of linked list;

public V get(Object key) {
    Node<K, V> e;
    return (e = getNode(hash(key), key)) == null ? null : e.value;
}

final Node<K, V> getNode(int hash, Object key) {
    Node<K, V>[] tab;
    Node<K, V> first, e;
    int n;
    K k;
    // If the number of buckets is greater than 0 and the first element of the bucket where the key to be found is located is not empty
    if ((tab = table) != null && (n = tab.length) > 0 &&
            (first = tab[(n - 1) & hash]) != null) {
        // Check whether the first element is the element to be checked. If so, return it directly
        if (first.hash == hash && // always check first node
                ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
        if ((e = first.next) != null) {
            // If the first element is a tree node, look it up as a tree
            if (first instanceof TreeNode)
                return ((TreeNode<K, V>) first).getTreeNode(hash, key);

            // Otherwise, it will traverse the whole linked list to find the element
            do {
                if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null);
        }
    }
    return null;
}

TreeNode.getTreeNode(int h, Object k) method - > search method of red black tree

(1) Here is to start the comparison from the root node of the tree, and then determine according to the size of the comparison result. Continue to find the left subtree. If found, return.

final TreeNode<K, V> getTreeNode(int h, Object k) {
    // Find from the root node of the tree
    return ((parent != null) ? root() : this).find(h, k, null);
}

final TreeNode<K, V> find(int h, Object k, Class<?> kc) {
    TreeNode<K, V> p = this;
    do {
        int ph, dir;
        K pk;
        TreeNode<K, V> pl = p.left, pr = p.right, q;
        if ((ph = p.hash) > h)
            // Left subtree
            p = pl;
        else if (ph < h)
            // Right subtree
            p = pr;
        else if ((pk = p.key) == k || (k != null && k.equals(pk)))
            // Direct return found
            return p;
        else if (pl == null)
            // The hash es are the same but the key s are different. The left subtree is empty. Check the right subtree
            p = pr;
        else if (pr == null)
            // The right subtree is empty. Check the left subtree
            p = pl;
        else if ((kc != null ||
                (kc = comparableClassFor(k)) != null) &&
                (dir = compareComparables(kc, k, pk)) != 0)
            // Compare the size of the key value through the compare method to determine whether to use the left subtree or the right subtree
            p = (dir < 0) ? pl : pr;
        else if ((q = pr.find(h, k, kc)) != null)
            // If none of the above conditions pass, try to find it in the right subtree
            return q;
        else
            // If you can't find them, just look in the left subtree
            p = pl;
    } while (p != null);
    return null;
}

remove(Object key) method - > delete elements according to key

(1) Locate the bucket according to the hash value of the key;

(2) Traverse and search according to the linked list or red black tree;

(3) If the found node is a tree node, it will be treated as the removed node of the tree;

(4) If the found node is the first node in the bucket, move the second node to the first position;

(5) Otherwise, delete the node according to the linked list;

(6) Modify the size, call the post-processing after removing the node, etc;

public V remove(Object key) {
    Node<K, V> e;
    return (e = removeNode(hash(key), key, null, false, true)) == null ?
            null : e.value;
}

final Node<K, V> removeNode(int hash, Object key, Object value,
                            boolean matchValue, boolean movable) {
    Node<K, V>[] tab;
    Node<K, V> p;
    int n, index;
    // If the number of buckets is greater than 0 and the first element of the bucket where the element to be deleted is located is not empty
    if ((tab = table) != null && (n = tab.length) > 0 &&
            (p = tab[index = (n - 1) & hash]) != null) {
        Node<K, V> node = null, e;
        K k;
        V v;
        if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
            // If the first element is exactly the element to be found, assign it to the node variable and delete it later
            node = p;
        else if ((e = p.next) != null) {
            if (p instanceof TreeNode)
                // If the first element is a tree node, the node is found as a tree
                node = ((TreeNode<K, V>) p).getTreeNode(hash, key);
            else {
                // Otherwise, traverse the entire linked list to find elements
                do {
                    if (e.hash == hash &&
                            ((k = e.key) == key ||
                                    (key != null && key.equals(k)))) {
                        node = e;
                        break;
                    }
                    p = e;
                } while ((e = e.next) != null);
            }
        }
        // If the element is found, check whether the parameter needs to match the value value. If it does not need to match, delete it directly. If it needs to match, check whether the value value is equal to the passed in value
        if (node != null && (!matchValue || (v = node.value) == value ||
                (value != null && value.equals(v)))) {
            if (node instanceof TreeNode)
                // If it is a tree node, call the delete method of the tree (if it is called with node, delete itself)
                ((TreeNode<K, V>) node).removeTreeNode(this, tab, movable);
            else if (node == p)
                // If the element to be deleted is the first element, move the second element to the first position
                tab[index] = node.next;
            else
                // Otherwise, delete the node node
                p.next = node.next;
            ++modCount;
            --size;
            // Post processing after deleting nodes
            afterNodeRemoval(node);
            return node;
        }
    }
    return null;
}

5, Frequently asked questions
1. How is the hash function of HashMap designed

HashMap's hash function is to first get the hashcode of the key, which is a 32-bit int type value, and then make the high 16 bits and low 16 bits of the hashcode XOR.

    static final int hash(Object key) {
        int h;
        // The hashCode of key and the hashCode of key are shifted to the right by 16 bits for XOR operation
        return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
    }

This is designed to reduce the probability of hash collision.

Because key The hashcode() function calls the hash function of the key value type and returns the int type hash value. The int value range is - 2147483648 ~ 2147483647, which adds up to about 4 billion mapping space.

As long as the hash function is mapped evenly and loosely, it is difficult to collide in general applications. But the problem is that an array with a length of 4 billion can't fit into memory.

If the initial size of the HashMap array is only 16, you need to modulo the length of the array before using the remainder to access the array subscript.

The modular operation in the source code is to do an "and &" operation on the hash value and array length - 1. The bit operation is faster than the remainder% operation.

bucketIndex = indexFor(hash, table.length);

static int indexFor(int h, int length) {
     return h & (length-1);
}

By the way, this also explains why the array length of HashMap should take an integer power of 2. Because this (array length - 1) is exactly equivalent to a "low mask". The result of the and operation is that all the high bits of the hash value return to zero, and only the low bits are reserved for array subscript access. Take the initial length 16 as an example, 16-1 = 15. The binary representation is 0000 0000 0000 0000 1111. And a hash value. The result is to intercept the lowest four digit value.

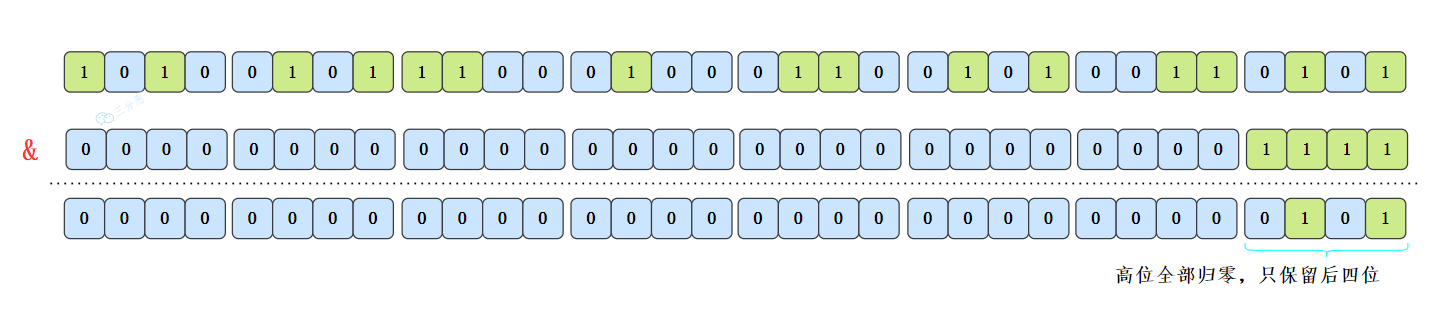
This is faster, but a new problem comes. Even if the hash value distribution is loose, if only the last few digits are taken, the collision will be very serious. If the hash itself is not well done, the loopholes in the equal difference sequence in the distribution will be even more difficult if the last few low bits are regularly repeated.

At this time, the value of the disturbance function is reflected. Take a look at the schematic diagram of the disturbance function:

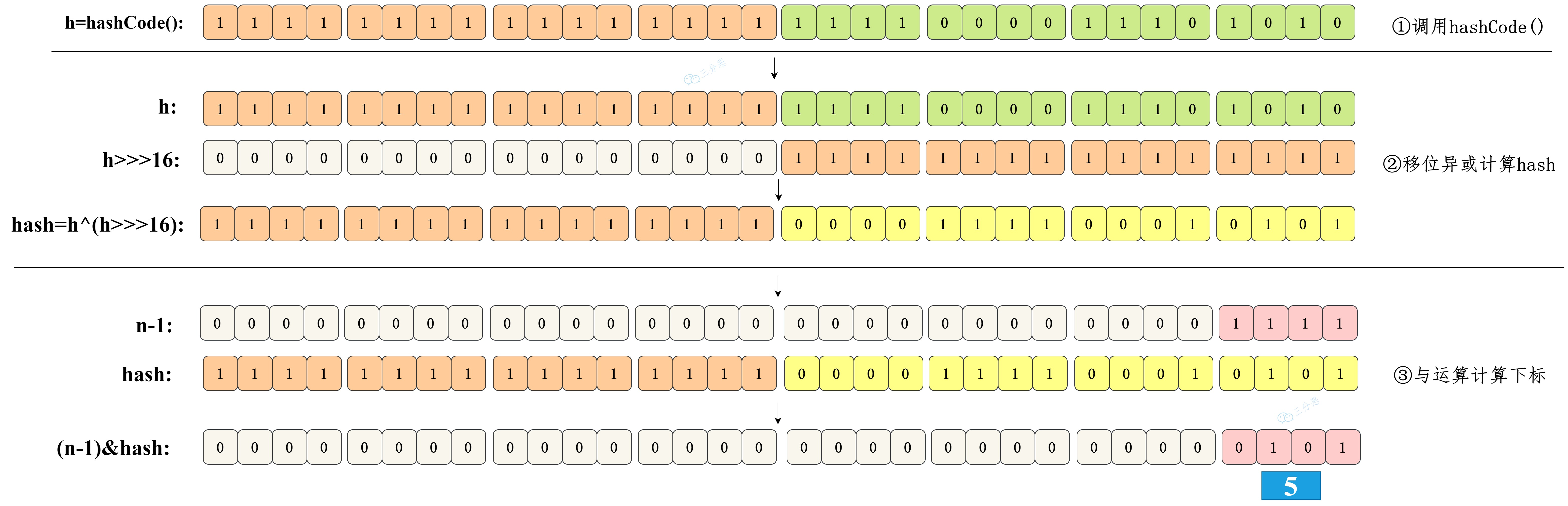
Shift 16 bits to the right, which is exactly half of 32bit. The purpose of XOR in its high half area and low half area is to mix the high and low bits of the original hash code, so as to increase the randomness of the low bits. Moreover, the mixed low-level is doped with some characteristics of the high-level, so that the high-level information is retained in disguise.

2. Why is the capacity of HashMap a multiple of 2?

• The first reason is to facilitate hash remainder:
  Placing elements on the table array uses the hash value% array size to locate the position, while HashMap uses the hash value & (array size - 1), which can achieve the same effect as before. This is due to the fact that the size of HashMap is a multiple of 2, which means that only one bit of the number is 1, and the number - 1 can get that the 1 on the binary bit becomes 0, and the subsequent 0 becomes 1, Through the & operation, we can get the same effect as% and the bit operation is much more efficient than% operation

• The second aspect is that during capacity expansion, the size after capacity expansion is also a multiple of 2 to perfectly transfer the elements that have generated hash collision to the new table
  We can simply take a look at the capacity expansion mechanism of HashMap. When the elements in HashMap exceed the load factor * HashMap size, capacity expansion will occur.

What are the ways to resolve hash conflicts?
Up to now, we know the reason why HashMap uses linked lists. In order to deal with hash conflicts, this method is called:

• Chain address method: pull a linked list at the conflicting position and put the conflicting elements in it.
  In addition, there are some common conflict resolution methods:

• Open addressing method: open addressing method is to find a space for the conflicting elements from the position of the conflict and then down.

There are also many ways to find free locations:

  - Line exploration method: Starting from the conflicting location, judge whether the next location is free in turn until the free location is found
  - Square probe method: From the location of the conflict x Start, add 1 for the first time^2 Two positions, 2 for the second time^2...，Until you find a free location

...

• Re hashing method: change the hash function to recalculate the address of the conflict element.
• Create a common overflow area: create another array and put the conflicting elements into it.

3. dk1.8. What are the main optimizations for HashMap? Why?

jdk1. The HashMap of 8 has five main optimizations:

-Data structure: array + linked list has been changed to array + linked list or red black tree

The reason is that it takes too long to change the complexity of the linked list from "hash" to "log o" in the linked list

-Linked list insertion method: the insertion method of linked list is changed from head insertion method to tail insertion method

In short, when inserting, if there are already elements in the array position, 1.7 put the new elements into the array, the original node as the successor node of the new node, 1.8 traverse the linked list, and place the elements at the end of the linked list.

Reason: 1.7 when the head insertion method is used to expand the capacity, the head insertion method will reverse the linked list and generate rings in a multithreaded environment.

-Capacity expansion rehash: during capacity expansion, 1.7 needs to rehash the elements in the original array to the position of the new array. 1.8 uses simpler judgment logic and does not need to re calculate the position through the hash function. The new position remains unchanged or the index + new capacity.

Reason: improve the efficiency of capacity expansion and expand capacity faster.

• Capacity expansion opportunity: when inserting, 1.7 first determines whether capacity expansion is required, and then inserts; 1.8 first inserts, and then determines whether capacity expansion is required after insertion is completed;

• Hash function: 1.7 does four shifts and four exclusive or, jdk1 8 only once.

Reason: if you do it four times, the marginal utility is not large. Change it to one time to improve efficiency.

4. Why is the threshold of HashMap linked list to red black tree 8?
The size of red black tree nodes is about twice that of ordinary nodes, so turning to red black tree sacrifices space for time. It is more a bottom-up strategy to ensure the search efficiency in extreme cases.

Why choose 8 for the threshold? It's about statistics. Ideally, using random hash code, the nodes in the linked list conform to Poisson distribution, and the probability of the number of nodes is decreasing. When the number of nodes is 8, the probability of occurrence is only 0.00000006.

Why is the threshold of red black tree back to linked list 6 instead of 8? This is because if the threshold is also set to 8, if there is a collision and the increase or decrease of nodes is just around 8, the continuous conversion of linked list and red black tree will occur, resulting in a waste of resources.

reference resources:

I suggest you go to the original blog, which is detailed and good.

Counter attack by flour dregs: HashMap soul chasing 23 questions
HashMap source code analysis