This article talks about a common interview question, jdk1 8 How is the HashMap capacity expansion rehash algorithm optimized?
As we all know, the bottom layer of HashMap is actually an array. Since it is an array, the inevitable length is fixed, so there must be a problem of capacity expansion. At jd.k1 7 is to double the capacity of the array, then re hash all the key s in the HashMap, and then put them into the new position of the new array after capacity expansion.
But from jdk1 After 8, rehash is optimized to reduce the process of re hashing the key. How to implement it is up to the source code.
We all know that HashMap expansion is realized through resize, so let's take a look at the implementation of resize method
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
//This newcap = oldcap < < 1 is the evidence of double capacity expansion
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
//Rebuild a new array with the capacity of newCap calculated above
//It's twice the size
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
//Get the old array, then traverse the position of each array and rehash each node
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
//When traversing to the position of this array, there is a node, enter rehash again
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
//This simply means that there is only one node
//That is, when no linked list or red black tree is formed
//At this time, the processing is to re hash the addressing algorithm and find the location of the new array
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
//This is already a red black tree. At this time, it will enter the process of red black tree rehash
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
//This is the rehash process of the linked list
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
In fact, rehash is to traverse each position of the array and judge the state of the node, which is a single or linked list or red black tree. Next, discuss each case.
1) Single node
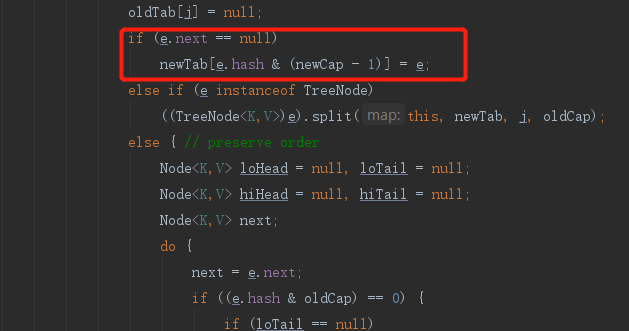
In fact, re hash addressing algorithm, find the subscript of the corresponding array and put it on the line
2) Linked list
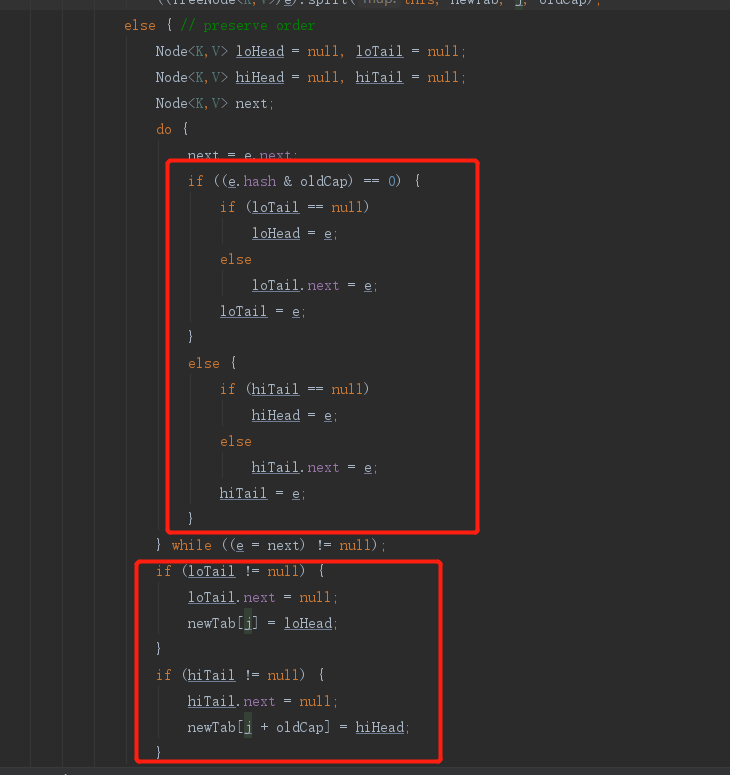
After carefully reading the source code, you will find that the previous linked list rehash is re divided into two linked lists. One linked list rehash is still in the current position index, and the position after the other linked list rehash becomes index + oldCap. Draw a diagram to understand
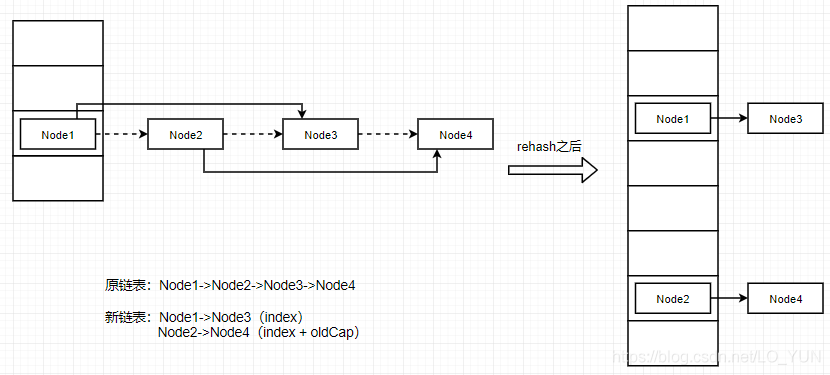
As for why it can be divided into two linked lists, here's an explanation. When the hash addressing algorithm recalculates all nodes of an array subscript after capacity expansion, it will find that the calculated position is either the original index or the original index + oldCap. This is a feature of hash addressing, so based on this established conclusion, Just judge whether each node is in the original position or the position of index + oldCap after re hashing (how to judge, it is the first red box in the source code diagram). Judge whether it is in the original position, and then a new linked list will be formed at the position of index + oldCap, After this calculation, just hang the two new linked lists on the index and index + oldCap of the new array (how to hang is the second red box in the source code diagram). This avoids the process of re hashing each node and putting it back into the hash table, which greatly improves the efficiency, that is, jdk1 8 HashMap expansion rehash algorithm optimization.
3) Red black tree
Paste the source code
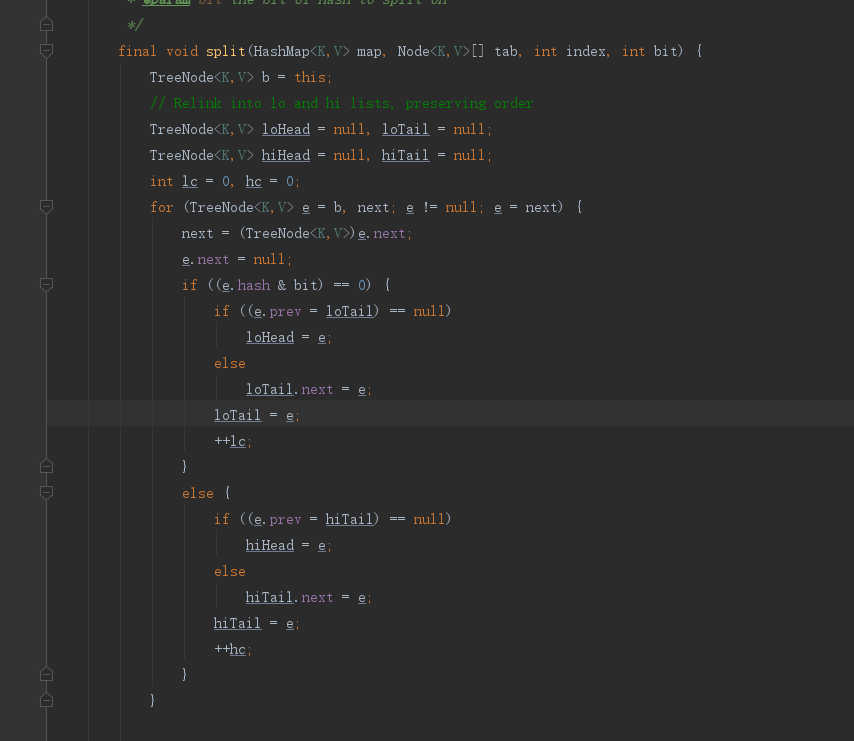
In fact, the principle is similar to that of the linked list, that is, the linked list is divided into two linked lists, and the red black tree is divided into two red black trees, which are respectively hung on the position of the new array, but the last judgment is to judge whether the red black tree needs to become a linked list or continue to be a red black tree.
So in jdk1 The rehash algorithm optimization of 8 is to split the original linked list or red black tree into two parts, and then hang them respectively at the position of the original array and the position of the array + oldCap. This avoids the process of rehash addressing algorithm and rehash of a large number of nodes, and greatly increases the capacity expansion efficiency.
End of this article.
If my article is helpful to you, please pay attention, like, watch and forward it. Your support will encourage me to output higher quality articles. Thank you very much!
If you want to contact me, welcome to my personal WeChat official account java diary, and release technical articles every day, and you can add my WeChat ZZYNKXJH to contact me. I look forward to making progress with you.