1. Find out the duplicate numbers in the array

Title Link: https://www.acwing.com/problem/content/14/

Idea 1: sorting

ac Code: time complexity O ( n × l o g n ) O(n\times logn) O(n×logn)
Idea: here is to sort the array, and then compare two adjacent elements. If they are equal, the number will be returned directly.

class Solution {
public:
    int duplicateInArray(vector<int>& nums) {
        if(nums.empty()) return -1;
        int n = nums.size();
        sort(nums.begin(), nums.end());
        if(nums[0] < 0 || nums[n - 1] > n - 1) return -1;
        for(int i = 0; i < n - 1; i ++){
            if(nums[i + 1] == nums[i]) return nums[i];
        }
        return  -1;
    }
};

Idea 2: hash table

Use the unordered container in C + +_ Map counts the number of elements. If the number of elements is greater than 1, it can be output directly.

ac Code: time complexity O ( n × l o g n ) O(n\times logn) O(n × logn), spatial complexity O ( 1 ) O(1) O(1) because a hash table with length n is used.

class Solution {
public:
    int duplicateInArray(vector<int>& nums) {
        int n = nums.size();
        unordered_map<int, int> mp;
        for(int i = 0; i < n; i ++)
            if(nums[i] < 0 || nums[i] > n -1) return -1;
        for(int i = 0; i < n; i ++){
            mp[nums[i]] ++;
            if(mp[nums[i]] > 1) return nums[i];
        }
        return -1;
    }
};

Idea 3: in situ exchange

Time complexity O ( n ) O(n) O(n), spatial complexity O ( 1 ) O(1) O(1).

Idea: will x = n u m s [ i ] x=nums[i] x=nums[i] and subscript x x Value at x n u m s [ x ] nums[x] Compare nums[x]. If different, exchange nums[i] and nums[x], so that the value x can be placed in the place of subscript X. The next time x appears and finds x = = n u m s [ x ] x == nums[x] When x==nums[x], X is the value that appears twice.

The popular explanation is that the legal position of the value 2 is where the subscript is 2. If it is elsewhere, it needs to be exchanged to the legal position (the index is 2). When will this process end? Until 2 appears at other index positions, that is, duplication occurs; Or exchange n times, but there is no repetition, and the algorithm stops.

For example, if the value 2 is in the index 0 0 0, and n u m s [ 2 ] = = 2 nums[2] == 2 nums[2]==2. At this time, that is, 2 repeats. Just return 2.

The better explanation here is the analogy of "one radish, one pit" in the leetcode problem solution.

class Solution {
public:
    int duplicateInArray(vector<int>& nums) {
        if(nums.empty()) return -1;
        int n = nums.size();
        for(int i = 0; i < n; i ++)
            if(nums[i] < 0 || nums[i] > n - 1) return -1;
        for(int i = 0; i < n; i ++){
            while(i != nums[i] && nums[i] != nums[nums[i]]) 
                swap(nums[i], nums[nums[i]]);
            if(i != nums[i] && nums[i] == nums[nums[i]]) return nums[i];
        }
        return  -1;
    }
};

A little introduction

class Solution {
public:
    int duplicateInArray(vector<int>& nums) {
        int n = nums.size();
        for(auto &x : nums) if(x < 0 || x > n - 1) return -1;
        for(int i = 0; i < n; i ++){
            int x = nums[i];
            while( x != i && x != nums[x]) swap(x, nums[x]);
            if(x != i && x == nums[x]) return x;
        }
        return -1;
    }
};

2. Do not modify the array to find duplicate numbers

Title Link: https://www.acwing.com/problem/content/15/

Idea: drawer principle + dichotomy

This question requires that the original array cannot be modified

Problem solving ideas

We use dichotomy here. Since each number is between 1 and N, and there are n+1 numbers in total, at least one number is repeated. This is based on the drawer principle.

Drawer principle:
If n+1 items are put in n drawers, at least one drawer will put 2 items.

For the string of data with the maximum value of n-1, we divide it into two segments, namely a = [ 1 , n 2 ] a=[1, \frac{n}{2}] a=[1,2n] and b = [ n 2 + 1 , n ] b=[\frac{n}{2}+1,n] b=[2n​+1,n]. Please note that this is a binary of the logarithm, not an array subscript. Later, we will count the number of values in this interval.

For example, if the maximum value n-1 = 7, then the interval [ 1 , 7 ] [1,7] The interval of [1,7] points is a = [ 1 , 4 ] a=[1,4] a=[1,4] and b = [ 5 , 7 ] b=[5,7] b=[5,7]. Then traverse the array and count the number of numbers in two intervals. Among them, the number of numbers in one interval must be greater than the length of the interval. Suppose this interval is a = [ 1 , 4 ] a=[1, 4] a=[1,4], its interval length is 4 - 1 + 1 = 4, and it is assumed that the number of elements in a counted in the original array is 5. According to the drawer principle, there must be duplicate values in this interval. Then we can divide the interval [ 1 , 7 ] [1,7] [1,7] reduced to [ 1 , 4 ] [1,4] [1,4], and then repeat the above steps until the length of an interval becomes 1. At this time, this value is the answer.

• Time complexity O ( n l o g n ) O(nlogn) O(nlogn): This is because the length of the array is halved each time l o g n logn Log n times, and the whole array needs to be traversed each time, so the time complexity is n l o g n nlogn nlogn;

• Spatial complexity O ( 1 ) O(1) O(1), because other structures such as arrays or hash tables are not used.

acwing

ac code

class Solution {
public:
    int duplicateInArray(vector<int>& nums) {
        int l = 1, r = nums.size() - 1;
        while(l < r){
            int mid = l + r >> 1; // [l, mid], [mid + 1, r]
            int s = 0; // Number of left half edges
            for(auto x :nums) s += x >= l && x <= mid;
            if(s > mid - l + 1) r = mid;
            else l = mid + 1;
        }
        return r;
    }
};

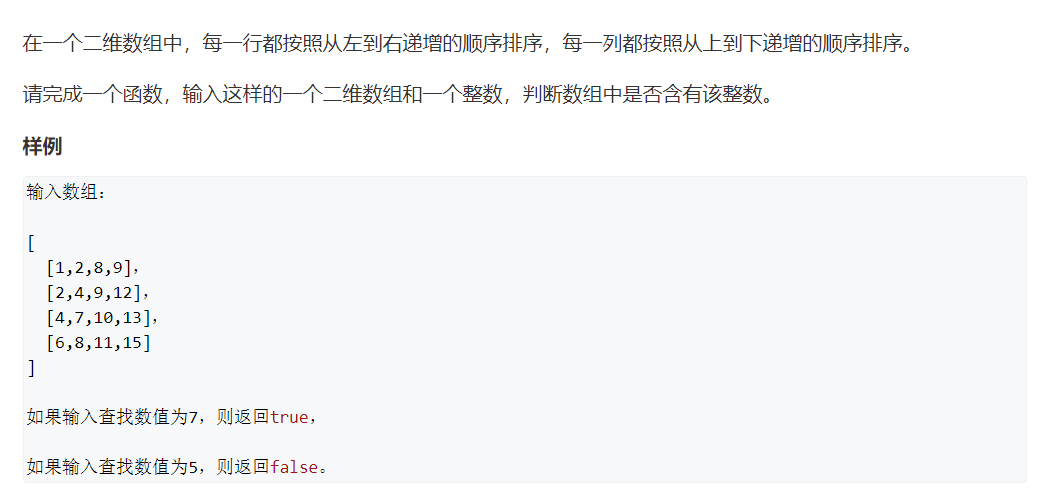
3. Search in two-dimensional array

Title Link: https://www.acwing.com/problem/content/16/

Idea: thinking question (select the value in the upper right corner)

Select the value a in the upper right corner of the grid every time. In this way, the row and column of the value form a monotonic sequence. If target < A, the column can be discarded; If target > A, the row can be discarded.

AC code

Time complexity O ( m + n ) O(m + n) O(m+n), where m and N are the dimensions of two-dimensional array and the spatial complexity O ( 1 ) O(1) O(1)

class Solution {
public:
    bool searchArray(vector<vector<int>> array, int target) {
        if(array.empty()) return false;
        int n =  array.size(), m = array[0].size();
        int i = 0, j = m - 1; // Coordinates of the upper right corner
        while(i < n && j >= 0){
            if(array[i][j] == target) return true;
            else if(target < array[i][j]) j--; // Delete the last column
            else i ++; //Delete the top line
        }
        return false;
    }
};

4. Replace spaces

Title Link: https://www.acwing.com/problem/content/17/

Idea: grammar questions

Open a new string res, traverse str, replace it with "% 20" when encountering spaces, and add it to the end of res. if it is not a space, add it to the end of res.

AC code

Time complexity O ( n ) O(n) O(n), spatial complexity O ( n ) O(n) O(n)

class Solution {
public:
    string replaceSpaces(string &str) {
        string res;
        for(auto &x : str){
            if(x == ' ') res += "%20";
            else res += x;
        }
        return res;
    }
};

5. Print the linked list from end to end

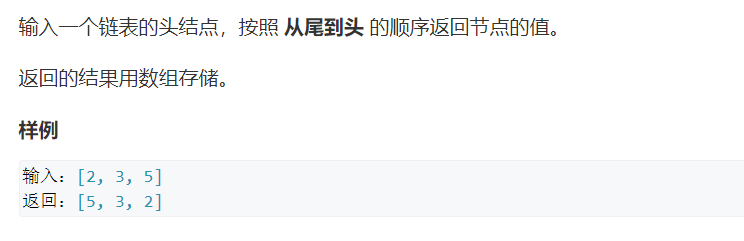
Traverse the linked list, put its elements into the vector (named RES) in turn, and then output the vector in reverse order. The reverse order here uses the reverse order iterator return vector < int > (res.rbegin(), res.rend());

Time complexity O ( n ) O(n) O(n), spatial complexity O ( n ) O(n) O(n)

AC code

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> printListReversingly(ListNode* head) {
        vector<int> res;
        while(head){
            res.push_back(head->val);
            head = head->next;
        }
        return vector<int>(res.rbegin(),res.rend());
    }
};

6. Rebuild binary tree

Title Link: https://www.acwing.com/problem/content/23/

thinking

According to the pre order traversal and middle order traversal of binary tree, the process of recursive tree building is mainly investigated.
dfs(pl, pr, il, ir) is used here
pl represents the left end point of preorder traversal, and pr represents the right end point of preorder traversal;
il represents the left end point of mid order traversal, and ir represents the right end point of mid order traversal.
The return value is the tree root.

Finally, you need to add root - > left = left and root - > right = right to the total root node to rebuild the binary tree.

Time complexity O ( n ) O(n) O(n), spatial complexity O ( n ) O(n) O(n)

AC code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    unordered_map<int, int> hash;// Hash table, which stores the location of the traversal data in the middle order
    vector<int> preorder, inorder;
    TreeNode* buildTree(vector<int>& _preorder, vector<int>& _inorder) {
        preorder = _preorder, inorder = _inorder;
        for(int i =0; i < inorder.size(); i ++) hash[inorder[i]] = i;
        return dfs(0, preorder.size() - 1, 0, inorder.size() - 1);
    }
    
    TreeNode* dfs(int pl, int pr, int il, int ir){
        if(pl > pr) return nullptr;
        auto root = new TreeNode(preorder[pl]); 
        int k = hash[root->val]; // Position in middle order traversal
        auto left = dfs(pl + 1, k - il + pl, il, k - 1);
        auto right = dfs(k - il + pl + 1, pr, k + 1, ir);
        root->left = left, root->right = right;
        return root;
    }
};

7. Next node of binary tree

Commonly known as "the successor of the tree"
Title Link: https://www.acwing.com/problem/content/31/

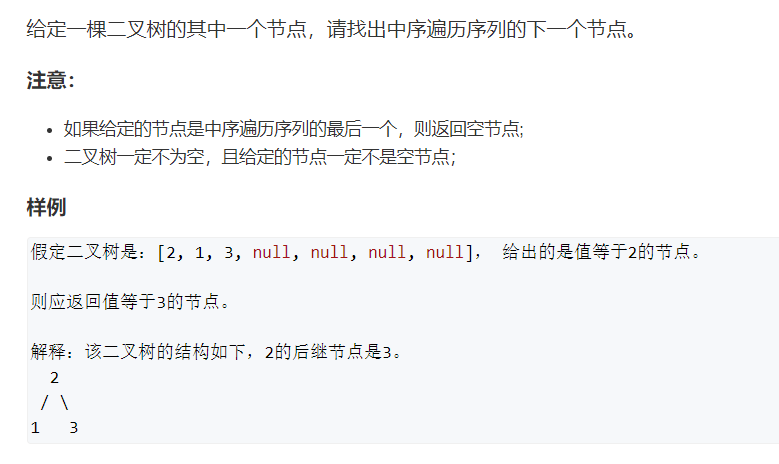
thinking

Time complexity O ( H ) O(H) O(H),H is the height and spatial complexity of the tree O ( 1 ) O(1) O(1)

The node source is discussed in two cases.

First, if the source node has a right subtree, the subsequent node of the middle order traversal is the leftmost point in the left subtree.

Second, the source node has no right subtree. How to deal with it at this time? You need to traverse up along the parent node until you find the first point. This point is the left son of its parent node. This point is marked as temp, and the parent node of this point is the successor of source.

For example, here we take node e as the source, which has no right subtree, which is obviously the second case. We traverse upward, source = e - > father, that is, source becomes B. at this time, we find that B is the left son of A, reaches the boundary condition, and A is the successor of E.

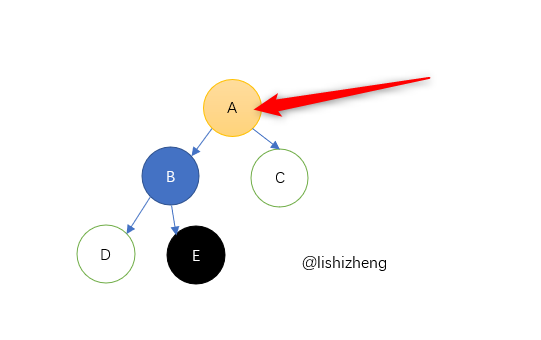
ac code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode *father;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL), father(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* p) {
        if(p->right){ //p-node has right subtree
            p = p->right;
            while(p->left) p = p->left;
            return p;
        }
        // p node has no right subtree
        // Traverse up and find that the first current point is the left son of the parent node
        while(p->father && p == p->father->right) p = p->father;
        return p->father;
    }
};

8. Implement queue with two stacks

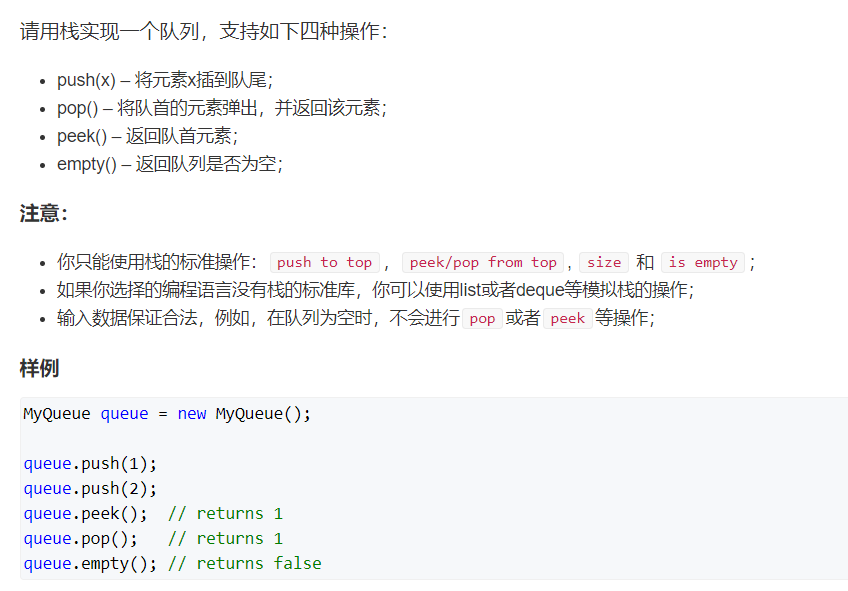
thinking

Two stacks are used to simulate queue behavior: queue first in first out.
Specific operation:
For the push operation of the queue, you can directly stack 1.
For the pop operation of the queue, pop all stack1 elements into stack2, and then top in stack2. After use, press all the elements in stack2 into stack1.

Spatial complexity O ( n ) O(n) O(n), time complexity:

• push yes O ( 1 ) O(1) O(1)
• pop is O ( n ) O(n) O(n)
• peek is O ( n ) O(n) O(n)
• empty yes O ( 1 ) O(1) O(1)

ac code

class MyQueue {
public:
    stack<int> stk, cache;
    /** Initialize your data structure here. */
    MyQueue() {
        
    }
    
    /** Push element x to the back of queue. */
    void push(int x) {
        stk.push(x);
    }
    
    void copy(stack<int> &a, stack<int> &b){
        while(a.size()){
            b.push(a.top());
            a.pop();
        }
    }
    
    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        copy(stk, cache);
        int res = cache.top();
        cache.pop();
        copy(cache, stk);
        return res;
    }
    
    /** Get the front element. */
    int peek() {
        copy(stk, cache);
        int res = cache.top();
        copy(cache, stk);
        return res;
    }
    
    /** Returns whether the queue is empty. */
    bool empty() {
        return stk.empty();
    }
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * bool param_4 = obj.empty();
 */

9. Fibonacci series

thinking

Open a large array, save the value of each index, traverse and recurs.
Time complexity O ( n ) O(n) O(n), spatial complexity O ( n ) O(n) O(n)

AC code

class Solution {
public:
    int a[39];
    int Fibonacci(int n) {
        a[1] = 1, a[2] = 1;
        for(int i = 3; i <= 39; i ++) a[i] = a[i - 1] + a[i - 2];
        return a[n];
    }
};

10. Rotate the minimum number of the array

Idea 1: Violence

Violent practices:
Time complexity O ( n ) O(n) O(n), spatial complexity O ( 1 ) O(1) O(1)

ac code

class Solution {
public:
    int findMin(vector<int>& nums) {
        if(nums.empty()) return -1;
        int res = nums[0];
        for(auto &x : nums) if(x <= res) res = x;
        return res;
    }
};

Idea 2: dichotomy

After the whole array is rotated, the trend is shown in the figure below.

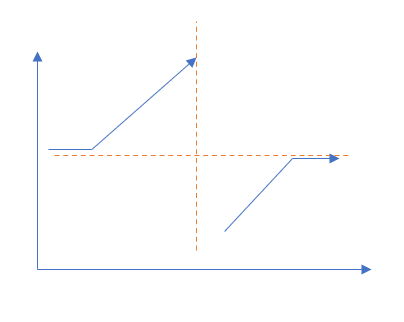
In the first half, meet n u m s [ i ] ≥ n u m s [ 0 ] nums[i] \ge nums[0] nums[i] ≥ nums[0], the latter half (excluding the last paragraph) may be equal to n u m s [ 0 ] nums[0] nums[0]) does not satisfy this property. The dividing point is the smallest value in the array.

You can use dichotomy to find the dividing point. The specific operation steps are as follows:

• Preprocess and delete the last paragraph n u m s [ 0 ] nums[0] Value of num [0].
• After deletion, if the last number is greater than n u m s [ 0 ] nums[0] nums[0], then the rest is a monotonically increasing sequence, and the minimum value is n u m s [ 0 ] nums[0] nums[0].
• After deletion, if the last number is less than n u m s [ 0 ] nums[0] nums[0], then conduct dichotomy to find the dividing point.

Dichotomous time complexity O ( l o g n ) O(logn) O(logn), delete the last paragraph. The worst case is O ( n ) O(n) O(n), so the total time complexity is O ( n ) O(n) O(n), spatial complexity O ( 1 ) O(1) O(1).

ac code

class Solution {
public:
    int findMin(vector<int>& nums) {
        if(nums.empty()) return -1;
        int n = nums.size() - 1;
        int a = nums[0];
        while(n > 0 && nums[n] == a)  n --;
        if(nums[n] >= a) return a;
        int l = 0, r = n;
        while(l < r){
            int mid = l + r >> 1; // [l, mid] and [mid + 1, r]
            if(nums[mid] < a) r = mid;
            else l = mid + 1;
        }
        return nums[r];
        
    }
};

11. Path in matrix

Title Link: https://www.acwing.com/problem/content/21/

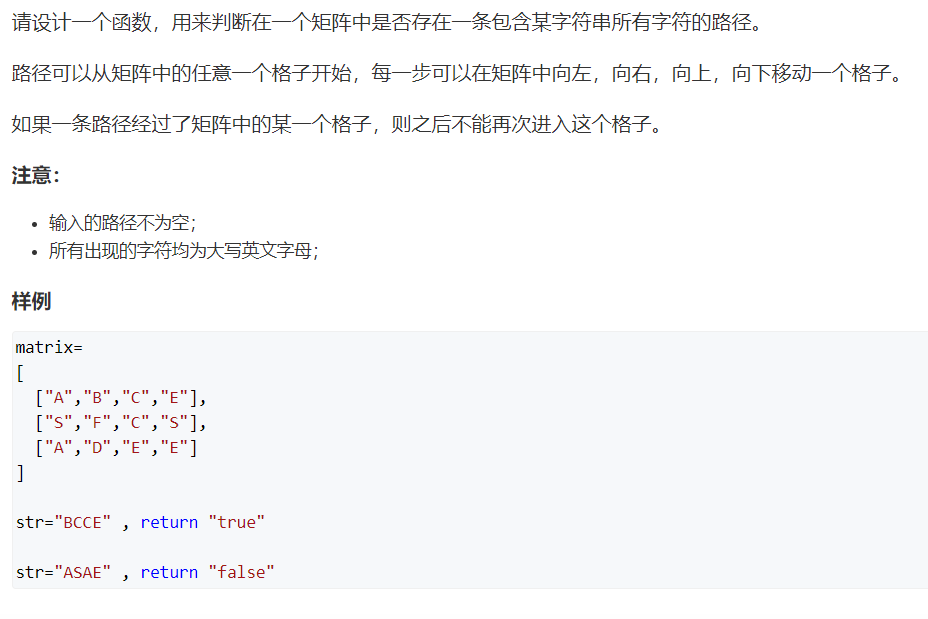
thinking

Depth first search dfs
Enumeration string starting point, total n 2 n^2 n2, and then whether each starting point dfs can form a character path. Note that you can't go back in dfs search.

Time complexity O ( n 2 k 3 ) O(n^2 k^3) O(n2k3),k is the number of str characters - 1, space complexity O ( 1 ) O(1) O(1)

class Solution {
public:
    bool hasPath(vector<vector<char>>& matrix, string &str) {
        if(matrix.empty()) return false;
        int n = matrix.size(), m = matrix[0].size();
        for(int i = 0; i < n; i ++)
            for(int j = 0; j < m; j ++)
                if(dfs(matrix, str, 0, i, j)) return true;
        return false;
    }
    
    bool dfs(vector<vector<char>>& matrix, string &str, int u, int x, int y){
        if(u == str.size()) return true;
        if(matrix[x][y] != str[u]) return false;
        //Special judgment matrix = a, and str = a
        if(matrix[x][y] == str[u] && u == str.size() - 1) return true;
        char t = matrix[x][y];
        matrix[x][y] = '%';
        int dx[4] ={1, 0, -1, 0}, dy[4] = {0, 1, 0, -1};
        for(int i = 0; i < 4; i ++){
            int a = x + dx[i], b = y + dy[i];
            if(a >= 0 && a < matrix.size() && b >= 0 && b <matrix[0].size()){
                if(dfs(matrix, str, u + 1, a, b)) return true;
            }
        }
        matrix[x][y] = t; // Restore the site
        return false;
    }
};

summary

After brushing a certain amount of questions and seeing a certain amount of models, the feeling of brushing questions is cultivated. Almost everyone has to take this step.