Introduction to Joseph:

It is said that Josephus, a famous Jewish historian, had the following story: 39 Jews hid in a cave with Josephus and his friends after the Roman occupation of Chotapat. 39 Jews decided to die rather than be caught by the enemy, so they decided to commit suicide. 41 people lined up in a circle and were opened by the first one. At the beginning of each report, the third person must commit suicide, and then the next re-report, until all the people committed suicide. Josephus and his friends, however, did not want to comply. Start with one person, cross k-2 people (because the first person has been crossed), and kill the k-person. Then, cross the k-1 and kill the k-1. This process continues along the circle until at last only one person remains, and the person can continue to live. The question is, given peace, where do you stand to avoid execution in the first place? Josephus wanted his friend to pretend to obey first. He arranged his friend and himself in the 16th and 31st places, and escaped the death game.

Programming Description:

There are N children in a circle hand in hand. They start counting from the first M child and report to the K child. Then they continue counting from the next child. They ask: The order of all the children in the queue?
The following picture:

The data structure of Joseph problem leads to:
Fig. 1-1: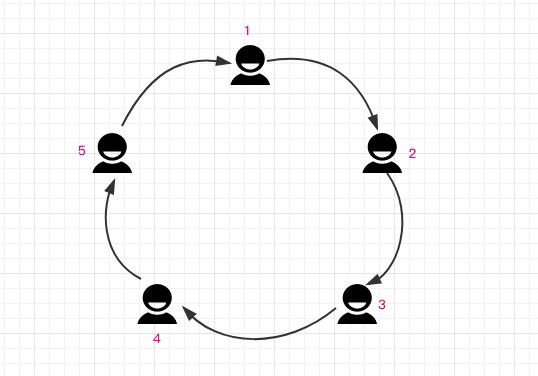

Question: What data structure is appropriate to deal with this problem?
We might as well deal with Figure 1-1 a little, as shown in Figure 1-2 below:

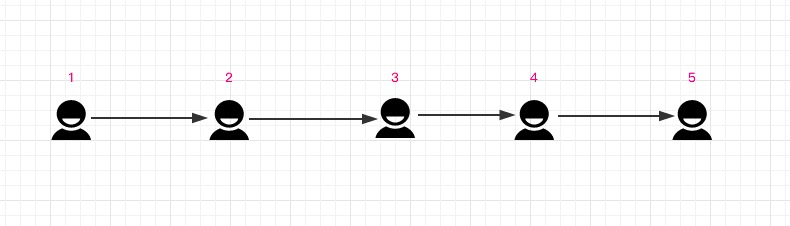
If we look at each person as a node node, each node has a pointer pointing to the next node, we can easily think of a data structure is a one-way list, if we link the end of the single list with the head, the tail pointing to the head is Figure 1-1, it is very suitable to solve this Joseph. So we can use one-way ring list data structure to simulate and solve the problem.

Implementation of Data Structure
The basic categories are as follows:
Child-like mock children:

class Child {

    private int no;

    private Child next;

    public Child(int no) {
        this.no = no;
    }

    public int getNo() {
        return no;
    }

    public void setNo(int no) {
        this.no = no;
    }

    public Child getNext() {
        return next;
    }

    public void setNext(Child next) {
        this.next = next;
    }
}

CircleSingleLinkedList-like analogue Joseph rings:

class CircleSingleLinkedList {
    private Child head;

    public void init(int n) {
        //todo
      

    }


    public void show() {
        //todo
    }

    public void delete(int no) {
        //todo
    }
}

CircleSingleLinkedList method implementation:

1. Initialize the creation of Joseph rings with N nodes:
   Analysis: We just need to point the next of the last node to the next node, and the next of the last node to the first one.

public void init(int n) {
        Child cur;
        if (n < 1) {
            return;
        } else if (n == 1) {
            child = new Child(1);
            child.setNext(child);
        } else {
            child = new Child(1);
            child.setNext(child);
            cur = child;
            for (int i = 2; i <= n; i++) {
                cur = cur.getNext();
                Child cd = new Child(i);
                cur.setNext(cd);
                cd.setNext(child);
            }
        }

    }

2. Print Joseph Ring:
Analysis: Traveling through each node from the beginning, when the node's getNext()==head, the traversal ends, which is equivalent to traversing to the last one.

public void show() {
        if (head == null) {
            return;
        }
        if (head.getNext() == head) {
            System.out.println(head.getNo());
            return;
        }
        Child cur = head;
        while (cur.getNext() != head) {
            System.out.println(cur.getNo());
            cur = cur.getNext();

        }
        System.out.println(cur.getNo());
    }

3. Adding a node to Joseph Ring to the end:
Analysis: Traveling from the first node to the last one, the next of the last node is pointed to the added node, and the next of the added node is pointed to the head of the head node.

public void addLast(Child child) {
        Child cur = head;
        while (cur.getNext() != head) {
            if (cur.getNo()==child.getNo()){
                throw new RuntimeException("Number already exists!!");
            }
            cur = cur.getNext();
        }
        if (cur.getNo()==child.getNo()){
            throw new RuntimeException("Number already exists!!");
        }
        cur.setNext(child);
        child.setNext(head);
    }

4. Delete a Joseph ring node:
Traversing the Joseph Ring, finding the last node of the node to be deleted, pointing the next node of the previous node to the next node of the node to be deleted can be done, but if it is the deleted head node, the next node of the head node needs to be designated as the head node.

public void delete(int no) {
        if (head == null) {
            return;
        }
        Child cur = head;
        while (cur.getNext() != head) {
            if (cur.getNext().getNo() == no) {
                cur.setNext(cur.getNext().getNext());
                return;
            }
            cur = cur.getNext();
        }
        if (cur.getNext().getNo() == no) {
            cur.setNext(cur.getNext().getNext());
            head = cur.getNext();
        }

    }

So far, the data structure and basic methods of Joseph rings are as follows:

class CircleSingleLinkedList {
    private Child head;

    public void init(int n) {
        Child cur;
        if (n < 1) {
            return;
        } else if (n == 1) {
            head = new Child(1);
            head.setNext(head);
        } else {
            head = new Child(1);
            head.setNext(head);
            cur = head;
            for (int i = 2; i <= n; i++) {
                cur = cur.getNext();
                Child cd = new Child(i);
                cur.setNext(cd);
                cd.setNext(head);
            }
        }

    }

    public void addLast(Child child) {
        Child cur = head;
        while (cur.getNext() != head) {
            if (cur.getNo()==child.getNo()){
                throw new RuntimeException("Number already exists!!");
            }
            cur = cur.getNext();
        }
        if (cur.getNo()==child.getNo()){
            throw new RuntimeException("Number already exists!!");
        }
        cur.setNext(child);
        child.setNext(head);
    }


    public void show() {
        if (head == null) {
            return;
        }
        if (head.getNext() == head) {
            System.out.println(head.getNo());
            return;
        }
        Child cur = head;
        while (cur.getNext() != head) {
            System.out.println(cur.getNo());
            cur = cur.getNext();

        }
        System.out.println(cur.getNo());
    }

    public void delete(int no) {
        if (head == null) {
            return;
        }
        Child cur = head;
        while (cur.getNext() != head) {
            if (cur.getNext().getNo() == no) {
                cur.setNext(cur.getNext().getNext());
                return;
            }
            cur = cur.getNext();
        }
        if (cur.getNext().getNo() == no) {
            cur.setNext(cur.getNext().getNext());
            head = cur.getNext();
        }

    }
}

Solving Joseph Problem in Joseph Ring Data Structure
We start counting from beginNo, and every time we start counting readNum, how do we get out of the team?
Analysis: Beginning with beginNo as a game, it is equivalent to the first node of mobile Joseph ring, and beginNo as the first node. We need an auxiliary pointer to queue, which initially points to the tail node. The number of reports is equivalent to the number of mobile head nodes and auxiliary pointers. When the head node arrives at the node in the queue, the next of the auxiliary pointer points to the head node and the next of the auxiliary pointer completes the queue. Next of the auxiliary pointer is then used as the head node until only the last node is left. And the head node and the auxiliary pointer point to the same node.

public void josephPop(int beginNo, int readNum) {
        if (head == null) {
            return;
        }
        Child helper = head;
        while (true) {
            if (helper.getNext() == head) {
                break;
            }
            helper = helper.getNext();
        }
        for (int i = 1; i < beginNo; i++) {
            head = head.getNext();
            helper = helper.getNext();
        }
        while (head != helper) {
            for (int i = 0; i < readNum - 1; i++) {
                head = head.getNext();
                helper = helper.getNext();
            }
            System.out.println(head.getNo());
            helper.setNext(head.getNext());
            head = helper.getNext();
        }

        System.out.println(helper.getNo());

    }

So far, Joseph Ring and Joseph Problem are simulated as follows:

class CircleSingleLinkedList {
    private Child head;

    public void init(int n) {
        Child cur;
        if (n < 1) {
            return;
        } else if (n == 1) {
            head = new Child(1);
            head.setNext(head);
        } else {
            head = new Child(1);
            head.setNext(head);
            cur = head;
            for (int i = 2; i <= n; i++) {
                cur = cur.getNext();
                Child cd = new Child(i);
                cur.setNext(cd);
                cd.setNext(head);
            }
        }

    }

    public void addLast(Child child) {
        Child cur = head;
        while (cur.getNext() != head) {
            if (cur.getNo()==child.getNo()){
                throw new RuntimeException("Number already exists!!");
            }
            cur = cur.getNext();
        }
        if (cur.getNo()==child.getNo()){
            throw new RuntimeException("Number already exists!!");
        }
        cur.setNext(child);
        child.setNext(head);
    }


    public void show() {
        if (head == null) {
            return;
        }
        if (head.getNext() == head) {
            System.out.println(head.getNo());
            return;
        }
        Child cur = head;
        while (cur.getNext() != head) {
            System.out.println(cur.getNo());
            cur = cur.getNext();

        }
        System.out.println(cur.getNo());
    }

    public void delete(int no) {
        if (head == null) {
            return;
        }
        Child cur = head;
        while (cur.getNext() != head) {
            if (cur.getNext().getNo() == no) {
                cur.setNext(cur.getNext().getNext());
                return;
            }
            cur = cur.getNext();
        }
        if (cur.getNext().getNo() == no) {
            cur.setNext(cur.getNext().getNext());
            head = cur.getNext();
        }

    }

    public void josephPop(int beginNo, int readNum) {
        if (head == null) {
            return;
        }
        Child helper = head;
        while (true) {
            if (helper.getNext() == head) {
                break;
            }
            helper = helper.getNext();
        }
        for (int i = 1; i < beginNo; i++) {
            head = head.getNext();
            helper = helper.getNext();
        }
        while (head != helper) {
            for (int i = 0; i < readNum - 1; i++) {
                head = head.getNext();
                helper = helper.getNext();
            }
            System.out.println(head.getNo());
            helper.setNext(head.getNext());
            head = helper.getNext();
        }

        System.out.println(helper.getNo());


    }
}

test
Create a Joseph ring with five nodes and start counting from the first node, each time counting three. The order of queue formation is as follows:

public static void main(String[] args) {
        CircleSingleLinkedList circleSingleLinkedList = new CircleSingleLinkedList();
        circleSingleLinkedList.init(5);
        circleSingleLinkedList.josephPop(1, 3);
    }

The order of formation is: 31.524