Get implementation – get the corresponding location element

The idea is the same as that of the single linked list!

code

// 7 get method -- it is not efficient. It can be divided equally. After all, there is a tail node!
DoublyLinkedList.prototype.get = function(position){
  if(position < 0 || position >= this.length) return null;
  let current = this.head;
  let index = 0;
  while(index++ < position){
    current = current.next;
  }
  return current.data;
}

Here, novices will not write the code divided equally. The idea is to compare position with length/2. If it is greater than, use tail and if it is less than, use head!

indexOf implementation – determines whether an element is included

This is also the same as the idea of single linked list!

code

DoublyLinkedList.prototype.indexOf = function(data){
  let current = this.head;
  let index = 0;
  while(current){
    if(current.data === data){
      return index;
    }
    current = current.next;
    index++;
  }
  return -1;
}

update implementation – change the value of a location

Here rookies use the idea of bisection. Readers who don't use bisection can learn from here!

code

// 9 update method
DoublyLinkedList.prototype.update = function(position,data){
  if(position < 0 || position >= this.length) return false;
  if(position < this.length/2){
    let current = this.head;
    let index = 0;
    while(index++ < position){
      current = current.next;
    }
    current.data = data;
  }else{
    let current2 = this.tail;
    // Note: index is equal to length-1. Because length is the length and the subscript starts from 0, the maximum index can only be length-1
    let index = this.length - 1;
    while(index-- > position){
      current2 = current2.prev;
    }
    current2.data = data;
  }
  return true;
}

removeAt implementation – removes elements from a location

There are many situations here, eg:

1. Only one node
2. The second node is removed
3. The last node is removed
4. Remove intermediate node

2. 3. The reason for this is to change the direction of head and tail!

At the beginning, rookies wrote their own code without considering so many situations. Then they thought of it when watching the video, so they wrote it with their own ideas and the video.

code

// 11 removeAt1 video method
DoublyLinkedList.prototype.removeAt1 = function(position){
  if(position < 0 || position >= this.length) return false;
  // Determine whether there is only one node
  if(this.length === 1){
    this.head = null;
    this.tail = null;
  }else {
    if(position === 0){ //Judge whether the deleted node is the first node
      this.head.next.prev = null;
      this.head = this.head.next;
    }else if(position === this.length - 1){ // Judge whether the deleted node is the last node
      this.tail.prev.next = null;
      this.tail = this.tail.prev;
    }else{
      // Bisection idea
      if(position < this.length/2){
        let current = this.head;
        let index = 0;
        while(index++ < position - 1){
          current = current.next;
        }
        current.next.neaxt.prev = current;
        current.next = current.next.next;
      }else{
        let current = this.tail;
        let index = this.length - 1;
        while(index-- > position+1){
          current = current.prev;
        }
        current.prev.prev.next = current;
        current.prev =current.prev.prev;
      }
    }
  }

  this.length -= 1;
  return true;
}

Rookies here have different ideas from the video. They save the previous or the next node to be deleted, not the deleted node itself, so they can't return a value, but they feel better about the video (saving the deleted node). Because the two-way linked list is not like the one-way linked list, it needs to save the information of two nodes, because it can access both the previous node and the rear node!

Video code

remove implementation – removes a value

Here, just call two methods directly, and the rookie won't write

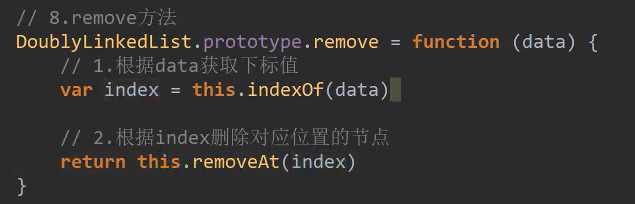
Other methods

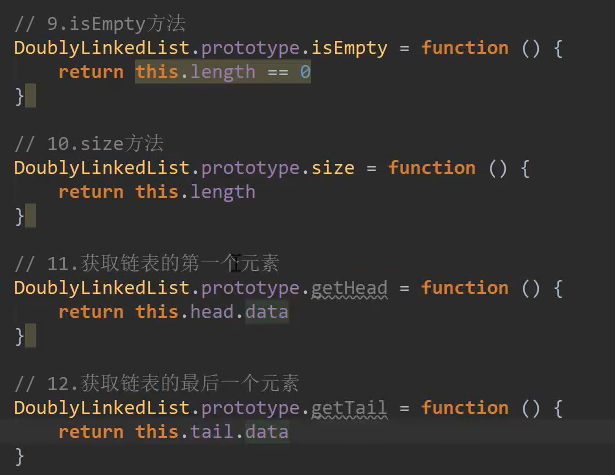
summary

In fact, it is not difficult to find that the difficulties of one-way linked lists and two-way linked lists lie in the insert and removeAt methods. As long as we understand some special situations of these two methods, it is not particularly difficult to write them; Other operations of the two-way linked list are really no different from the one-way linked list. Some are even simpler because of the tail pointer!