Time complexity & space complexity
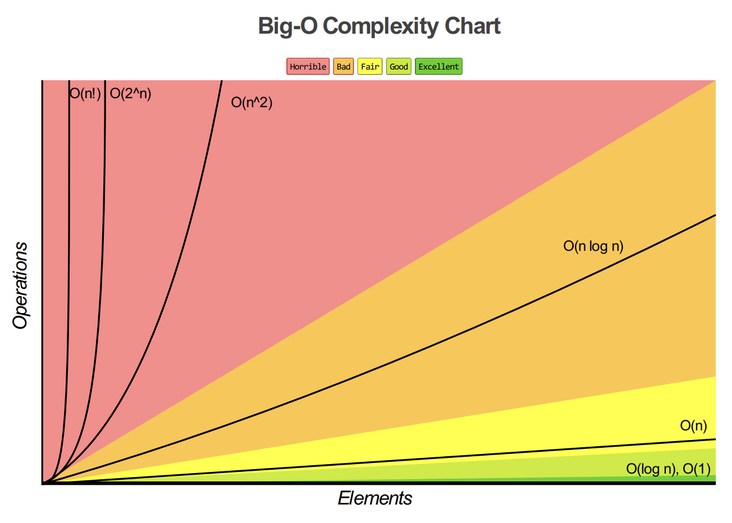
It can be seen from the figure that the time complexity should be controlled below O(nlogn).
Space complexity is a measure of the amount of storage space temporarily occupied by an algorithm during operation
According to their characteristics, js sorting can be roughly divided into two types: comparison sort and non comparison sort.
- Comparison sort: the relative order between elements is determined by comparison, and its time complexity cannot exceed O(nlogn), so it is also called nonlinear time comparison sort.
- Non comparison sort: it does not determine the relative order between elements through comparison. It can break through the time lower bound based on comparison sort and run in linear time. Therefore, it is also called linear time non comparison sort.
Comparison class sorting
Exchange sort
- Bubble sorting
- Quick sort
- Insert sort
Select sort
- Normal selection sort
- Heap sort
- Merge sort
Bubble sorting
Contact the first sorting algorithm, the logic is relatively simple
let testArr = [1, 3, 5, 3, 4, 54, 2423, 321, 4, 87];
function bubbleSort(arr) {
const len = arr.length
if (len < 2) return arr;
for (let i = 0; i < len; i++) {
for (let j = 0; j < i; j++) {
if (arr[j] > arr[i]) {
const tmp = arr[j];
arr[j] = arr[i]
arr[i] = tmp
}
}
}
return arr
}Quick sort
The basic idea of quick sort is to divide the records to be arranged into two independent parts through one-time sorting. If the keywords of one part of the records are smaller than those of the other part, the records of the two parts can be sorted separately to achieve the order of the whole sequence.
The main idea is to pick out an element from the sequence, It is called "pivot"; then reorder the sequence, and all elements smaller than the benchmark value are placed in front of the benchmark and those larger than the benchmark value are placed behind the benchmark; after this distinction is completed, the benchmark is in the middle of the sequence; then, the sub sequence (left) of elements smaller than the benchmark value and the sub sequence of elements larger than the benchmark value (right) recursively call the quick method to complete sorting, which is the idea of fast scheduling.
function quickSort(array) {
let quick = function (arr) {
if (arr.length <= 1) return arr;
// Math.floor() returns the largest integer less than or equal to a given number
// Gets the median index value of the array
const index = Math.floor(arr.length >> 1)
// Fetch index value
const pivot = arr.splice(index, 1)[0]
const left = []
const right = []
for (let i = 0; i < arr.length; i++) {
if (arr[i] > pivot) {
right.push(arr[i])
} else if (arr[i] <= pivot) {
left.push(arr[i])
}
}
return quick(left).concat([pivot], quick(right))
}
const result = quick(array)
return result
}Insert sort
A simple and intuitive sorting algorithm. Its working principle is to build an ordered sequence, scan the unordered data from back to front in the sorted sequence, find the corresponding position and insert it, so as to achieve the effect of sorting.
function insertSort(array) {
const len = array.length
let current // Current value
let prev // Previous value index
// Starting from 1, get the current value and compare it with the previous value. If the previous value is greater than the current value, exchange it
for (let i = 1; i < len; i++) {
// Record the current value
current = array[i]
prev = i - 1;
while (prev >= 0 && array[prev] > current) {
array[prev + 1] = array[prev]
prev--
}
array[prev + 1] = current
}
return array
}Select sort
Selective sorting is a simple and intuitive sorting algorithm. Its working principle is to first store the smallest element at the beginning of the sequence, then continue to find the smallest element from the remaining unordered elements, and then put it behind the sorted sequence... And so on until all elements are sorted. One of the most stable sorting algorithms, because no matter what data goes in, it is O(n square) time complexity, so when it is used, the smaller the data scale, the better
function selectSort(array) {
const len = array.length
let tmp;
let minIdx;
for (let i = 0; i < len - 1; i++) {
minIdx = i;
for (let j = i + 1; j < len; j++) {
if (array[j] < array[minIdx]) {
minIdx = j
}
}
tmp = array[i]
array[i] = array[minIdx]
array[minIdx] = tmp
}
return array
}Heap sort
Heap sort is a sort algorithm designed by using heap data structure. Heap is a structure similar to a complete binary tree and satisfies the nature of heap at the same time, that is, the key value or index of the child node is always less than (or greater than) its parent node. The bottom layer of the heap is actually a complete binary tree, which can be realized by array. The heap with the largest root node is called large root heap, and the heap with the smallest root node is called small root heap.
Core point
- The core point of heap sorting is to build a heap before sorting;
Since the heap is actually a complete binary tree, if the sequence number of the parent node is n, the sequence number of the leaf node is 2n and 2n+1 respectively
function heapSort(arr) { let len = arr.length // Build heap function buildMaxHeap(arr) { // The last one with child nodes starts building the heap for (let i = Math.floor(len / 2 - 1); i >= 0; i--) { // Heap adjustment is performed for each non leaf node maxHeapify(arr, i) } } function swap(arr, i, j) { [arr[j], arr[i]] = [arr[i], arr[j]] } function maxHeapify(arr, i) { let left = 2 * i + 1; let right = 2 * i + 2 // i is the root node of the subtree let largest = i; if (left < len && arr[left] > arr[largest]) { largest = left } if (right < len && arr[right] > arr[largest]) { largest = right } // When one of the above two judgments takes effect if (largest !== i) { swap(arr, i, largest) // After the exchange, arr[i] sinks and continues to adjust maxHeapify(arr, largest) } } buildMaxHeap(arr) for (let i = arr.length - 1; i > 0; i--) { swap(arr, 0, i) len--; maxHeapify(arr, 0) } return arr }Merge sort
Merge sort is an effective sort algorithm based on merge operation. This algorithm is a very typical application of divide and conquer method. The ordered subsequences are combined to obtain a completely ordered sequence; Each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are merged into one, it is called two-way merging.
function mergeSort(arr) { const merge = (right, left) => { const result = [] let idxLeft = 0 let idxRight = 0 while (idxLeft < left.length && idxRight < right.length) { if (left[idxLeft] < right[idxRight]) { result.push(left[idxLeft++]) } else { result.push(right[idxRight++]) } } while (idxLeft < left.length) { result.push(left[idxLeft++]) } while (idxRight < right[idxRight]) { result.push(right[idxRight++]) } return result } const mergeSort = arr => { if (arr.length === 1) return arr const mid = Math.floor(arr.length / 2) const left = arr.slice(0, mid) const right = arr.slice(mid, arr.length) return merge(mergeSort(left), mergeSort(right)) } return mergeSort(arr) }Merge sort is a stable sort method. Like selective sort, the performance of merge sort is not affected by the input data, but its performance is much better than selective sort, because it is always O(nlogn) time complexity. The cost is the need for additional memory space.
Time complexity, space complexity comparison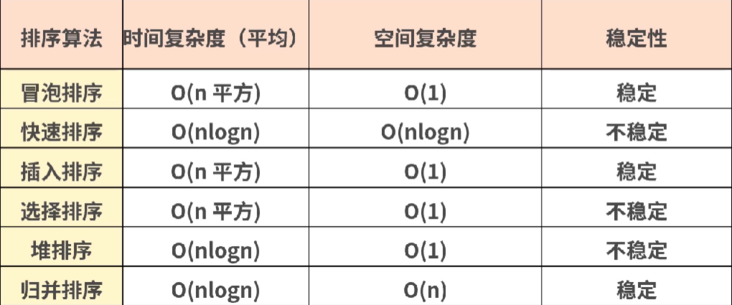
Sort method in Array
arr.sort([compareFunction])
compareFunction is used to specify the functions arranged in a certain order. If not written, the elements are sorted according to the Unicode sites of each character converted to a string
const months = ['March', 'Jan', 'Feb', 'Dec']; months.sort(); console.log(months) // [ 'Dec', 'Feb', 'Jan', 'March' ] const testArr = [1, 3, 5, 6, 3, 4, 54, 2423, 321, 4, 87]; testArr.sort(); console.log(testArr) // [1, 2423, 3, 3, 321, 4, 4, 5, 54, 6, 87]
If the compareFunction parameter is specified, the array will be sorted according to the return value of calling the function, that is, a and b are the two elements to be compared:
- If compareFunction (a, b) is less than 0, a will be arranged before B;
- If △ compareFunction (a, b) is equal to 0, the relative positions of a and B remain unchanged;
- If the compareFunction (a, b) is greater than 0, B will be arranged before a.
Analysis of the underlying sort source code
- When n < = 10, insert sorting is adopted;
- When n > 10, three-way quick sorting is adopted;
- 10 < n < = 1000, using the median as the sentinel element;
- n> 1000, pick out an element every 200 ~ 215 elements, put it into a new array, and then sort it to find the number in the middle, which is used as the median.
1. Why do you use insert sorting when the number of elements is small?
Although insertion sort is theoretically an algorithm with an average time complexity of O(n^2), quick sort is an algorithm with an average O(nlogn) level. But don't forget, this is only the theoretical average time complexity estimation, but they also have the best time complexity, and the insertion sort has the best time complexity of O(n).
In practice, there will be a coefficient in front of the complexity of both algorithms. When n is small enough, the advantage of fast sorting nlogn will be smaller and smaller. If the n of the insertion sort is small enough, it will exceed the fast row. In fact, this is the case. After the insertion sorting is optimized, it will have very superior performance for the sorting of small data sets, and sometimes even exceed the fast sorting. Therefore, for a small amount of data, applying insert sorting is a very good choice.
2. Why do you choose sentinel elements with so much effort?
Because the performance bottleneck of quick sorting lies in the depth of recursion. The worst case is that each sentinel is the smallest element or the largest element, so one side of the partition (one side is the element smaller than the sentinel, and the other side is the element larger than the sentinel) will be empty. If this row goes on, the number of recursive layers will reach n, and the complexity of each layer is O(n), Therefore, fast scheduling will degenerate into O(n^2) level at this time.
This situation should be avoided as much as possible, so how to avoid it? That is to make the sentinel element in the middle of the array as much as possible, and make the maximum or minimum cases as few as possible.
function ArraySort(comparefn) {
CHECK_OBJECT_COERCIBLE(this, "Array.prototype.sort");
var array = TO_OBJECT(this);
var length = TO_LENGTH(array.length);
return InnerArraySort(array, length, comparefn);
}
function InnerArraySort(array, length, comparefn) {
// Comparison function not passed in
if (!IS_CALLABLE(comparefn)) {
comparefn = function (x, y) {
if (x === y) return 0;
if ( % _IsSmi(x) && % _IsSmi(y)) {
return %SmiLexicographicCompare(x, y);
}
x = TO_STRING(x);
y = TO_STRING(y);
if (x == y) return 0;
else return x < y ? -1 : 1;
};
}
function InsertionSort(a, from, to) {
// Insert sort
for (var i = from + 1; i < to; i++) {
var element = a[i];
for (var j = i - 1; j >= from; j--) {
var tmp = a[j];
var order = comparefn(tmp, element);
if (order > 0) {
a[j + 1] = tmp;
} else {
break;
}
}
a[j + 1] = element;
}
}
function GetThirdIndex(a, from, to) { // When the number of elements is greater than 1000, look for sentinel elements
var t_array = new InternalArray();
var increment = 200 + ((to - from) & 15);
var j = 0;
from += 1;
to -= 1;
for (var i = from; i < to; i += increment) {
t_array[j] = [i, a[i]];
j++;
}
t_array.sort(function (a, b) {
return comparefn(a[1], b[1]);
});
var third_index = t_array[t_array.length >> 1][0];
return third_index;
}
function QuickSort(a, from, to) { // Quick sort implementation
//Sentry position
var third_index = 0;
while (true) {
if (to - from <= 10) {
InsertionSort(a, from, to); // Small amount of data, using insert sorting, fast
return;
}
if (to - from > 1000) {
third_index = GetThirdIndex(a, from, to);
} else {
// If it is less than 1000, take the midpoint directly
third_index = from + ((to - from) >> 1);
}
// Let's start fast
var v0 = a[from];
var v1 = a[to - 1];
var v2 = a[third_index];
var c01 = comparefn(v0, v1);
if (c01 > 0) {
var tmp = v0;
v0 = v1;
v1 = tmp;
}
var c02 = comparefn(v0, v2);
if (c02 >= 0) {
var tmp = v0;
v0 = v2;
v2 = v1;
v1 = tmp;
} else {
var c12 = comparefn(v1, v2);
if (c12 > 0) {
var tmp = v1;
v1 = v2;
v2 = tmp;
}
}
a[from] = v0;
a[to - 1] = v2;
var pivot = v1;
var low_end = from + 1;
var high_start = to - 1;
a[third_index] = a[low_end];
a[low_end] = pivot;
partition: for (var i = low_end + 1; i < high_start; i++) {
var element = a[i];
var order = comparefn(element, pivot);
if (order < 0) {
a[i] = a[low_end];
a[low_end] = element;
low_end++;
} else if (order > 0) {
do {
high_start--;
if (high_start == i) break partition;
var top_elem = a[high_start];
order = comparefn(top_elem, pivot);
} while (order > 0);
a[i] = a[high_start];
a[high_start] = element;
if (order < 0) {
element = a[i];
a[i] = a[low_end];
a[low_end] = element;
low_end++;
}
}
}
// The core idea of quick sorting is to recursively call the quick sorting method
if (to - high_start < low_end - from) {
QuickSort(a, high_start, to);
to = low_end;
} else {
QuickSort(a, from, low_end);
from = high_start;
}
}
}
}From the above source code analysis, insert sorting is used when the amount of data is less than 10; When the amount of data is greater than 10, three-way fast row is adopted; When the amount of data is 10 ~ 1000, the median is directly used as the sentinel element; When the amount of data is greater than 1000, start looking for sentinel elements.
Quick sort is unstable sort. The average and best time complexity are O(nlogn), the worst is O(n^2), and the space complexity is O(nlogn)
Insertion sort is a stable sort. The best time is O(n), the average and worst is O(n^2), and the space complexity is O(1)