Weekly test 5
describe
In two-dimensional plane, given n points {ai} and M points {bi}, it is guaranteed that the x coordinates or y coordinates of any two points in n+m points are different.
For each bi, the existence of a triangle consisting of three ai,aj,ak(1 < i,j,k < n,i J k) points containing Bi (also included on the edge of the triangle; a triangle with three collinear points is allowed, and only Bi is included on the line segment of any two points in the three points).
input
The first action is an integer n. Next, line n, where line i has two integers, representing the horizontal and vertical coordinates of ai.
The first action is an integer M. Next, line m, where line i has two integers, representing the horizontal and vertical coordinates of bi.
output
Output m lines, the i behavior of an integer 0 or 1, respectively, indicate whether there is a triangle containing the bi.
Sample 1 input

3
1 -6
-10 -1
0 6
3
-2 7
-4 -2
-3 1

Sample 1 output

0
1
1

Example 1 Interpretation
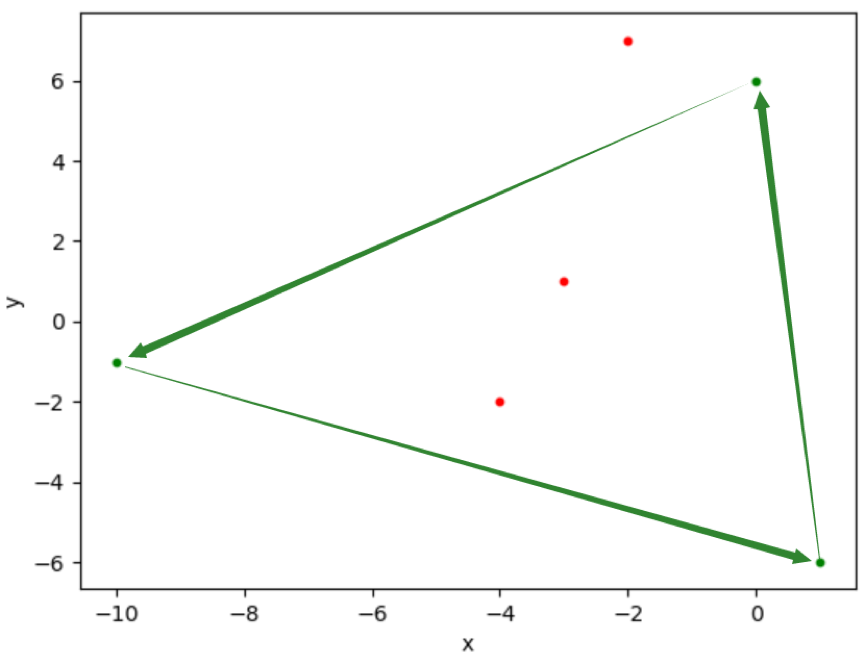
As shown in the figure, the green dot is A and the red dot is B. Red dots No. 2 and No. 3 are all contained in three green dots.

Example 2
See sample2_input.txt and sample2_output.txt and draw.py in the next file.
In order to facilitate debugging, I specially provided a draw.py file to draw point sets. You need to install python 3, and then
python3 -m pip install matplotlib
Final use
python3 draw.py
Run, copy the data in the question to get the picture. (You can redirect data, of course)
limit
n,m (> 3), coordinate absolute value no more than 109
30% of the data, n,m < 200;
Another 30% data, n,m < 2000;
The remaining 40% of the data, n,m < 300000.
Time: 3 sec
Space: 256 MB
Note that using Python classmates, OJ provides you with pypy to speed up, the source code does not need to change at all, just modify the first line to enjoy high-speed python.
To use pypy, you have to add (or use the IO template I gave you directly) to the first line.
python 2:
#!/usr/bin/env pypy
python 3:
#!/usr/bin/env pypy3
Tips
[Convex hull, you can refer to the code of "Convex hull" which is selected as the topic]
In order to help you complete the topic, we provide program templates that only contain input and output functions.
You can answer on the basis of these procedures, or not refer to them, depending on your actual situation, which has nothing to do with your score.
These programs can be downloaded from [here].

Method 1 Assistant Teaching Method:

1. Firstly, the upper and lower convex hulls are obtained, and then the two counter-clockwise directed edges e1 and e2 which intersect the upper and lower convex hulls with x=x0 are obtained by dichotomy (if they do not intersect, the red dots are not in the convex hulls).
2. Then determine whether the red dot (x0, y0) is on the left side of e1 and E 2 at the same time, if it is in the convex hull, otherwise it is not.
The time complexity is O((n+m)logn)

My method and code are as follows:
https://blog.csdn.net/qq_36782366/article/details/78161807

#include <vector>
#include <stdio.h>
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;


// ================= Code implementation begins=================

struct ip {
    int x, y, i;
    ip(int x = 0, int y = 0) : x(x), y(y), i(0) { }
    //Initialization list with the above equation as class
    void ri(int _i) {
        scanf("%d%d", &x, &y);
        i = _i;
    }
};

typedef ip iv;

const int N = 300005;
ip a[N], b[N], ch[N];
//a [] storage needs n pairs of points constituting convex hulls, and b [] storage needs to judge m pairs of points inside and outside. 
//convexhull,ch [] stores actual convex hull boundary points

// Compare the x-axis first and then the y-axis
bool operator < (const ip &a, const ip &b) {
    return a.x == b.x ? a.y < b.y : a.x < b.x;
}

// Overload minus sign, use a - b to calculate the vector subtracted by two points
iv operator - (const ip &a, const ip &b) {
    return ip(a.x - b.x, a.y - b.y);
}

// The cross product of a and b is calculated by a * b.
long long operator * (const iv &a, const iv &b) {
    return (long long)a.x * b.y - (long long)a.y * b.x;
}

int convex(ip *a, int n) {  
    //Ascending order
    sort(a,a+n);
    // n = unique(a,a+n)-a; / / / If there are repetitive points in the title, they must be de-duplicated
    
    int m=0;
    //Finding the Lower Convex Hull
    for(int i=0; i<n; ++i){
        for(; m>1 && ((ch[m-1]-ch[m-2])*(a[i]-ch[m-2])) < 0; --m);
        ch[m++] = a[i];
    }
    
    //Finding Upper Convex Hull
    for(int i=n-2, t=m; i>=0; --i){
        for(; m>t && ((ch[m-1]-ch[m-2])*(a[i]-ch[m-2])) < 0; --m);
        ch[m++] = a[i];
    }
    
    return m-1 ; 
    //Number of points whose return value is convex hull
}

//Here we explain the template to determine whether the point is in the convex hull:
//That is to take one of the points, he and other points can form n-2 triangles, using dichotomy to judge the product of difference.
//Judge whether he is in the current triangle, or on the left side of the triangle, or on the right side of the triangle, or outside the triangle.
int check(ip b,int n){
    int l=1,r=n-2,mid;
    while(l<=r)
    {
        mid=(l+r)>>1;
        long long a1=(ch[mid]-ch[0])*(b-ch[0]);  //Cross product of CH0 - > chmid and CH0 - > b
        long long a2=(ch[mid+1]-ch[0])*(b-ch[0]);//Cross product of CH0 - > chmid + 1 and CH0 - > b
        if(a1>=0&&a2<=0)    //That is to say, this point b is above or on the line of chmid, and below or on the line of chmid+1.
        {
            if((ch[mid+1]-ch[mid])*(b-ch[mid])>=0) //Cross product of chmid - > chmid + 1 and chmid - > b
                return true;        //If the cross product is greater than or equal to 0 at this time, it means that point b is inside or on the boundary of the triangle.
            return false;           //Conversely, the point is outside the triangle.
        }
        else if(a1<0)  //If the point is below chmid, then the upper boundary is reduced to mid-1.
        {
            r=mid-1; //The end point of dichotomy needs attention!
        }
        else //If the point is above chmid+1, then pull down the lower boundary to mid+1
        {
            l=mid+1;
        }
    }
    return false;
}

// Returns an array, representing the answer in turn
vector<int> getAnswer(int n, ip *a, int m, ip *b) {
    vector<int> ans;
    int mm = convex(a, n); //m is the length of the ch [] array
    for(int i=0; i<m; i++){
        int t=check(b[i],mm);        
        ans.push_back(t);       
    }
    return ans;
}


// ================= End of Code Implementation=================

int main() {
    int n, m;
    scanf("%d", &n);
    ip x;
    for (int i = 0; i < n; ++i)
        a[i].ri(i + 1);
    scanf("%d", &m);
    for (int i = 0; i < m; ++i)
        b[i].ri(i + 1);
        
    vector<int> ans = getAnswer(n, a, m, b);
    for (int i = 0; i < m; ++i)
        printf("%d\n", ans[i]);
    return 0;
}