Description

People's life not only depends on self struggle, but also considers the historical journey.
The journey of history can be abstracted into a 01 string. As an older person, you want to get some knowledge from the journey of history.
You find that one thing can be regarded as a prefix of 01 string, and the right position of the prefix is the end time of this thing.
The similarity of two things can be seen as the longest common suffix length of these two prefixes.
Now you're curious, what's the similarity between the two most similar things that end up in a range?

Input

The first line contains two positive integers, n,m, representing the string length and the number of queries.
The second line is a 01 string with a length of n, indicating the history of the journey.
Next m lines, each line has two positive integers l,r indicates that the query interval is from the first position to the r position, including the endpoint, ensuring that 1 < = l < = r < = n.

Output

Output m lines, and output an integer for each query to represent the maximum similarity.

Sample Input

4 2
0101
1 3
2 4

Sample Output

1
2

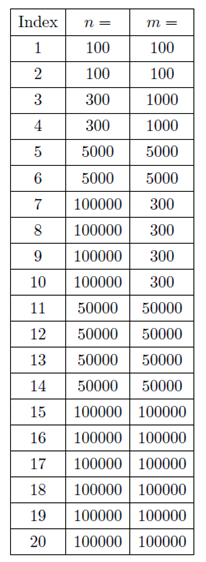
Data Constraint

thinking

Consider merging SA according to height from small to large, and maintain the queries in each block.
bitset, O(n ^ 2 / w)

Code

#include <bits/stdc++.h>
#pragma GCC optimize("Ofast")
#define mid (l + r >> 1)
#define ls (k << 1)
#define rs (k << 1 | 1)
using namespace std;

typedef set<int>::iterator I;
const int maxn = 100010;
int n, m, SZ, ans[maxn], rk[maxn], sa[maxn], mx[maxn << 2];
int ht[maxn], buc[maxn], sc[maxn], fa[maxn], id[maxn], cur[maxn];
char s[maxn];
vector<pair<int, int> > Q[maxn], M[maxn];
set<int> pos[maxn];
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
bool comp(int i, int j) { return ht[i] > ht[j]; }

void radix_sort() {
	for (int i = 1; i <= SZ; i++) buc[i] = 0;
	for (int i = 1; i <= n; i++) buc[rk[i]]++;
	for (int i = 1; i <= SZ; i++) buc[i] += buc[i - 1];
	for (int i = n; i; i--) sa[buc[rk[sc[i]]]--] = sc[i];
}

void calc_sa() {
	for (int i = 1; i <= n; i++) {
		rk[i] = s[i] - '0' + 1, sc[i] = i;
	}
	SZ = 2, radix_sort();
	for (int k = 1; k <= n; k <<= 1) {
		int cnt = 0;
		for (int i = n - k + 1; i <= n; i++) sc[++cnt] = i;
		for (int i = 1; i <= n; i++) {
			if (sa[i] > k) sc[++cnt] = sa[i] - k;
		}
		radix_sort(), swap(rk, sc), rk[sa[1]] = cnt = 1;
		for (int i = 2; i <= n; i++) {
			rk[sa[i]] = (sc[sa[i]] == sc[sa[i - 1]] &&
				sc[sa[i] + k] == sc[sa[i - 1] + k] ? cnt : ++cnt);
		}
		SZ = cnt; if (cnt == n) break;
	}
	for (int i = 1, j = 0; i <= n; i++) {
		if (rk[i] == 1) { j = ht[rk[i]] = 0; continue; }
		j = max(0, j - 1);
		while (s[sa[rk[i] - 1] + j] == s[i + j]) j++;
		ht[rk[i]] = j;
	}
}

void init() {
	for (int i = 1; i <= n; i++) {
		fa[i] = id[i] = i, pos[i].insert(i);
	}
	sort(id + 2, id + n + 1, comp);
	for (int i = 2; i <= n; i++) {
		int x = sa[id[i]], y = sa[id[i] - 1], len = ht[id[i]];
		int fx = find(x), fy = find(y);
		if (pos[fx].size() > pos[fy].size()) swap(fx, fy);
		for (I it1 = pos[fy].begin(); it1 != pos[fy].end(); it1++) {
			I it2 = pos[fx].insert(*it1).first, it3;
			if (it2 != pos[fx].begin()) {
				it3 = it2; it3--;
				if (find(*it2) != find(*it3)) {
					M[*it3].push_back(make_pair(*it2, len));
				}
			}
			it3 = it2; it3++;
			if (it3 != pos[fx].end() && find(*it2) != find(*it3)) {
				M[*it2].push_back(make_pair(*it3, len));
			}
		}
		fa[fy] = fx;
	}
}

void upd(int k, int l, int r, int p, int v) {
	if (l == r) { mx[k] = v; return; }
	if (mid >= p) upd(ls, l, mid, p, v);
	else upd(rs, mid + 1, r, p, v);
	mx[k] = max(mx[ls], mx[rs]);
}

int query(int k, int l, int r, int ql, int qr) {
	if (l >= ql && r <= qr) return mx[k];
	int ans = 0;
	if (mid >= ql) ans = max(ans, query(ls, l, mid, ql, qr));
	if (mid < qr) ans = max(ans, query(rs, mid + 1, r, ql, qr));
	return ans;
}

int main()
{
	freopen("history.in", "r", stdin);
	freopen("history.out", "w", stdout);
	scanf("%d %d %s", &n, &m, s + 1);
	reverse(s + 1, s + n + 1), calc_sa(), init();
	for (int i = 1, l, r; i <= m; i++)
	{
		scanf("%d %d", &r, &l);
		l = n - l + 1, r = n - r + 1;
		Q[l].push_back(make_pair(r, i));
	}
	for (int i = n; i; i--)
	{
		for (int j = 0; j < M[i].size(); j++)
		{
			cur[M[i][j].first] = max(cur[M[i][j].first], M[i][j].second);
			upd(1, 1, n, M[i][j].first, cur[M[i][j].first]);
		}
		for (int j = 0; j < Q[i].size(); j++)
		{
			ans[Q[i][j].second] = query(1, 1, n, i, Q[i][j].first);
		}
	}
	for (int i = 1; i <= m; i++)
	{
		printf("%d\n", ans[i]);
	}
	return 0;
}