This paper is a personal note made in the process of learning Kalman filter. Due to my poor mathematical skills, some views and understandings in this paper are only for readers' reference. If there are omissions, please don't hesitate to comment. Some references in this paper are from the following sources:
- <Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation>
- Principles of GNSS and inertial and multi-sensor integrated navigation system
- Introduction to driverless vehicle system (I) -- Kalman filter and target tracking https://blog.csdn.net/AdamShan/article/details/78248421
- Kalman filter - Wikipedia, free encyclopedia: https://zh.wikipedia.org/wiki/%E5%8D%A1%E5%B0%94%E6%9B%BC%E6%BB%A4%E6%B3%A2
- Covariance matrix - Wikipedia, free encyclopedia: https://zh.wikipedia.org/wiki/%E5%8D%8F%E6%96%B9%E5%B7%AE%E7%9F%A9%E9%98%B5
- What is the value of noise covariance matrix (R and Q) in Kalman filter and what is the relationship between noise distribution- Know the answer of "tea residue"
https://www.zhihu.com/question/53788909?sort=created - Five formulas of Kalman filter are derived from geerniya's blog CSDN blog
https://blog.csdn.net/geerniya/article/details/104804916
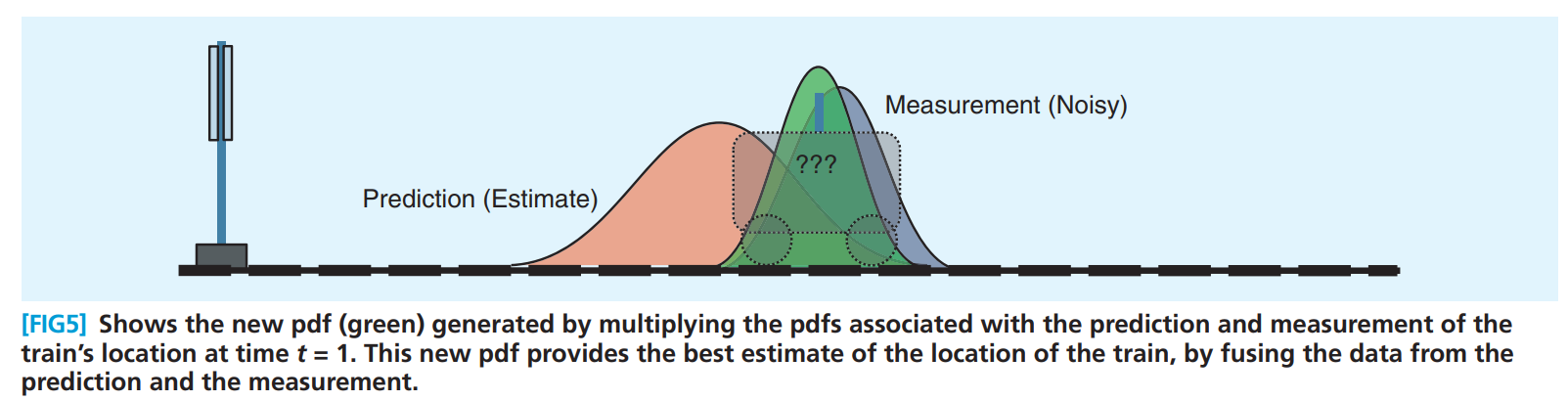
In essence, the process of Kalman filtering is to multiply the derived value of the "prediction model" with the probability distribution function (PDF) of the measured value to obtain the probability density function of the filtered result value. Of course, in theory, Kalman filtering can also be carried out without using prediction model and only using the measured values of two or more sensors. To infer the position of the car, for example, we know that it is $x_k Time moment of shape state ( position Set , speed degree etc. ) , through too Anticipate measure model type can with PUSH guide have to reach The state of time (position, speed, etc.) can be derived from the prediction model The state of time (position, speed, etc.) can be derived from the prediction model_ {k+1} Time moment of shape state . through too pass sense implement , I Guys can with measure amount have to reach one individual distance leave value The state of time. Through the sensor, we can measure a distance value The state of time. Through the sensor, we can measure a distance value z_k$. However, the error (noise) is everywhere, which leads to a certain deviation between our derived and measured values and the actual values, so that the derived and measured values of the trolley position are in a probability range. The idea of Kalman filter is to infer the probability range obtained in two ways to get a probability range closer to the actual value.
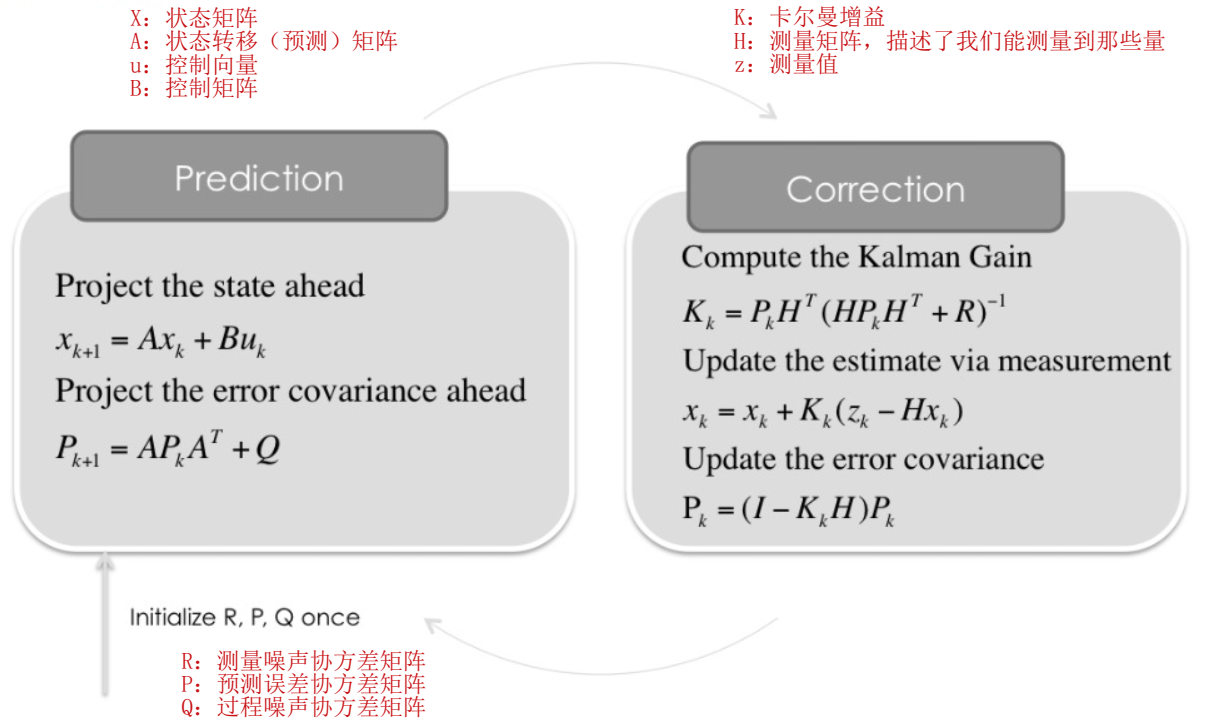
For ease of reference, the usual Kalman filter calculation process, that is, several familiar formulas, are posted here. It may be easier to understand if the picture is combined with the following text description.
1.1 - noise and error
If there is no noise and error, both the predicted value obtained by the prediction model and the measured value obtained by the sensor should be consistent with the actual value, that is, the current position of the trolley can be obtained 100%. Unfortunately, the existence of error and noise leads us to "guess" and "measure" the position of the car, which makes the results of prediction and measurement present a probability distribution. For example, 43.75% of the trolley may be 1.56m away from the starting point, and 12.28% may be 1.35m away from the starting point. The error of the prediction model usually comes from the deviation between the established theoretical model and the actual model. This part of the error is usually inevitable. After all, you can't consider all the influencing factors concretely and thoroughly. The measurement error of the sensor is relatively simple. It is usually related to your budget. The more expensive the sensor is, the higher the accuracy is and the more accurate the measurement value can be provided.
Although the actual error may be difficult to be represented by a standard mathematical method (such as white noise, Gaussian Markov process) or their combination, we can make the modeled error fully include the actual error. In other words, no matter how difficult it is to quantify the actual error, as long as its range does not exceed the error range of our modeling [2]. When modeling the error, we usually consider it as Gaussian noise, assume that its mean value is 0, obey the normal distribution, and use a covariance matrix [2,4,5] to represent it.
In Kalman filter, the error and noise are divided into three parts: the error between the predicted value (estimated value) and the actual value (true value) obtained by using the established prediction model, the prediction error; Measurement noise caused by error when measuring by sensor or other means; Process noise (or system noise) is the noise caused by some unmeasured motion process or unknown factors.
Covariance matrix of prediction error P P P (Error covariance matrix) is a symmetric matrix. The elements on the diagonal of the matrix are the estimation of the variance of the deviation between each state (such as the x and y coordinates of the position and the velocity in the x and y directions) and the actual value, and the elements on the non diagonal are the correlation between the prediction errors of different states. When the states can be estimated independently, the elements on the non diagonal line are 0. When we have less modeling information and can not estimate each state we need independently, these correlations can not be ignored. This problem is also called observability [2].
Covariance matrix of measurement noise R R R (measurement noise variance matrix) represents the expected value of the square of the measurement error and is a symmetric matrix. The diagonal elements of the matrix represent the variance of the error of each observation, and the non diagonal elements represent the correlation between the errors of different observations. In most applications, the observations are independent of each other, so the measurement error is small R R The covariance matrix of R is usually a diagonal matrix [2].
Covariance matrix of process noise Q Q Q is also called System noise covariance matrix, which is also a symmetric matrix [2]. It can be understood that some random noise is introduced during the change between the previous state and the next state. For example, when estimating the position of the trolley moving at a uniform speed on the track, some changes caused by the blockage of the air inlet or fuel pump nozzle will lead to short acceleration and deceleration of our trolley, and then introduce process noise.
It should be noted that the letters used to describe the error and noise here correspond to the Kalman filter calculation process diagram posted above. In some other documents or introductions, different letters may be used for representation. In summary, the covariance matrix of prediction error P P P reflects how uncertain you are about the value obtained from your prediction model. Measure the covariance matrix of noise R R R reflects the error of the sensor used in the measurement and the covariance matrix of the process noise Q Q Q covers many things, such as rounding error when using computer for calculation, degree of model linearization, etc [ 6 ] ^{[6]} [6]. These three errors need to be initialized during Kalman filtering. As mentioned above, although we can't know the exact range of error, as long as the actual error range is within our estimated error range.
If P 0 _0 0, Q and R cannot be obtained accurately. If only the possible value range is known, the possible larger value (conservative) shall be adopted. If you don't know exactly Q, R, P 0 _0 The value of Q should be appropriately increased to increase the utilization weight of real-time measured values, commonly known as tuning. However, there is blindness in tuning, and it is impossible to know how much Q should be adjusted.
——Principles of Kalman filter and integrated navigation, Qin Yongyuan [6] (? To be verified)
1.2 - Master, stop reading and give some examples
The following example comes from Adam Shan's blog: "Introduction to driverless vehicle system (I) -- Kalman filter and target tracking https://blog.csdn.net/AdamShan/article/details/78248421 ”, some modifications and adjustments have been made here
1.2.1 - Modeling
Taking the estimation of pedestrian motion state as an example, firstly, it is necessary to establish the representation of pedestrian state to be estimated, that is, the state matrix in the calculation process diagram of Kalman filter
x
x
x. here
x
k
+
1
x_{k+1}
xk+1 , represents the state at the current time,
x
k
x_k
xk , represents the state of the previous moment. If only the state of a pedestrian moving at a uniform speed in a two-dimensional plane is considered, the position in the x and y directions can be roughly used
p
p
p and velocity component
v
v
v means:
x
=
(
p
x
,
p
y
,
v
x
,
v
y
)
T
x=(p_x,p_y,v_x,v_y)^T
x=(px,py,vx,vy)T
After constructing the state representation, we also need to build a pedestrian motion model for reference. Through this model, we can infer the state of pedestrians at the next time, and also get the "prediction model" used in Kalman filter, that is, the left half of the calculation process diagram of Kalman filter. For uniform motion in a two-dimensional plane, a constant velocity model can be used:
x
k
+
1
=
A
x
k
+
ε
x_{k+1}=Ax_k+ε
xk+1=Axk+ε
In the formula
A
A
A is the matrix, that is, the description from the previous state
x
k
x_k
xk# how to move to the next state
x
k
+
1
x_{k+1}
The state transition matrix of xk+1;
ε
ε
ε Error introduced by process noise. In this simple example of uniform motion, the limited process noise only comes from the pedestrian moving in the x direction
a
x
a_x
ax , is the acceleration value, which is the same as that in the y direction
a
y
a_y
ay = acceleration and deceleration of acceleration value. It may be easier to understand the pedestrian model in matrix form, where
Δ
t
\Delta t
Δ t is the filtering step, or the calculated interval between states:
[
p
x
p
y
v
x
v
y
]
k
+
1
=
[
1
0
Δ
t
0
0
1
0
Δ
t
0
0
1
0
0
0
0
1
]
.
[
p
x
p
y
v
x
v
y
]
k
+
[
1
2
a
x
Δ
t
2
1
2
a
y
Δ
t
2
a
x
Δ
t
a
y
Δ
t
]
\begin{bmatrix} p_x\\p_y\\v_x\\v_y \end{bmatrix}_{k+1}=\begin{bmatrix} 1&0&\Delta t&0\\0&1&0&\Delta t\\0&0&1&0\\0&0&0&1 \end{bmatrix}.\begin{bmatrix} p_x\\p_y\\v_x\\v_y \end{bmatrix}_k+\begin{bmatrix} {1\over2}a_x\Delta t^2\\{1\over2}a_y\Delta t^2\\a_x\Delta t \\a_y\Delta t \end{bmatrix}
⎣⎢⎢⎡pxpyvxvy⎦⎥⎥⎤k+1=⎣⎢⎢⎡10000100Δt0100Δt01⎦⎥⎥⎤.⎣⎢⎢⎡pxpyvxvy⎦⎥⎥⎤k+⎣⎢⎢⎡21axΔt221ayΔt2axΔtayΔt⎦⎥⎥⎤
Expand to get:
{
p
x
k
+
1
=
p
x
+
v
x
k
Δ
t
+
1
2
a
x
Δ
t
2
p
y
k
+
1
=
p
y
+
v
y
k
Δ
t
+
1
2
a
y
Δ
t
2
v
x
k
+
1
=
v
x
+
a
x
Δ
t
v
y
k
+
1
=
v
y
+
a
y
Δ
t
\left \{ \begin{matrix} p_x^{k+1} = p_x+v_x^k\Delta t+{1\over2}a_x\Delta t^2\\p_y^{k+1} = p_y+v_y^k\Delta t+{1\over2}a_y\Delta t^2\\v_x^{k+1}=v_x+a_x\Delta t \\v_y^{k+1}=v_y+a_y\Delta t\end{matrix}\right.
⎩⎪⎪⎨⎪⎪⎧pxk+1=px+vxkΔt+21axΔt2pyk+1=py+vykΔt+21ayΔt2vxk+1=vx+axΔtvyk+1=vy+ayΔt
Obviously, it contains
a
x
a_x
ax , and
a
y
a_y
The term of ay is the error introduced by the uncertain acceleration in the default pedestrian uniform motion. In practical application, the process noise is unlikely to only come from a quantifiable interference term, and it is more common to combine the results of a variety of unmeasurable factors. Therefore, in the design process, the noise covariance matrix
Q
Q
Q, you can follow the suggestions mentioned above to make the actual error fall within the error range described by the model as far as possible.
Now that the general modeling of pedestrians has been completed, the next step is to start the construction and implementation of Kalman filter.
1.2.2 - Python implementation
In the state prediction step (Project the state ahead) of the Kalman filter calculation process diagram, B B B is the action on the control vector u u The input control model matrix on u, which describes the control vector u u u can actually act on the state matrix x x Which states of x and how it works. In this example, the pedestrian did not step on the balance car, nor did he install a rocket ejector behind him, but simply walked at a uniform speed. However, the internal muscle control of pedestrians cannot be dialyzed, which makes it impossible to B u Bu Bu makes a measurement. So in this case, B u Bu When Bu is set to 0, the formula of the state prediction step in the figure becomes x k + 1 = A x k x_{k+1}=Ax_k xk+1 = Axk, which is written in matrix form as follows:
[ p x p y v x v y ] k + 1 = [ 1 0 Δ t 0 0 1 0 Δ t 0 0 1 0 0 0 0 1 ] . [ p x p y v x v y ] k \begin{bmatrix} p_x\\p_y\\v_x\\v_y \end{bmatrix}_{k+1}=\begin{bmatrix} 1&0&\Delta t&0\\0&1&0&\Delta t\\0&0&1&0\\0&0&0&1 \end{bmatrix}.\begin{bmatrix} p_x\\p_y\\v_x\\v_y \end{bmatrix}_k ⎣⎢⎢⎡pxpyvxvy⎦⎥⎥⎤k+1=⎣⎢⎢⎡10000100Δt0100Δt01⎦⎥⎥⎤.⎣⎢⎢⎡pxpyvxvy⎦⎥⎥⎤k
x = np.matrix([[0.0, 0.0, 0.0, 0.0]]).T # X state matrix: x position, y position, X speed, y speed
print("the X is\n", x, x.shape)
dt = 0.1 # Time step between filter steps
A = np.matrix([[1.0, 0.0, dt, 0.0], # State transformation matrix (processing matrix) A
[0.0, 1.0, 0.0, dt],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0]])
print("------\nthe A is\n", A, A.shape)
The second step is to give the covariance matrix of the prediction error P P P. Covariance matrix of process noise Q Q Q. And the covariance matrix of measurement noise R R R. For prediction error covariance matrix P P P. You only need to give the initial value, which will be automatically updated in the subsequent Project the error covariance ahead.
For process noise covariance matrix
Q
Q
Q. As the example defines that the process noise only considers the impact of random acceleration and deceleration of pedestrians in x and y directions, and the acceleration in x and y directions is limited to the same scalar value, which conforms to the mean value of 0 and the standard deviation of 0
σ
a
σ_a
σ a) normal distribution of. Therefore, the process noise covariance matrix
Q
Q
Q. That is, in formula 2
ε
ε
ε The covariance matrix of can be expanded as follows [3,4]:
Q
=
c
o
v
(
ε
)
=
c
o
v
(
G
a
)
=
E
[
(
G
a
)
(
G
a
)
T
]
=
G
E
[
a
2
]
G
T
=
G
[
σ
a
2
]
G
T
=
[
σ
a
2
]
G
G
T
Q=cov(ε)=cov(Ga)=E[(Ga)(Ga)^T]=GE[a^2]G^T=G[σ_a^2]G^T=[σ_a^2]GG^T
Q=cov(ε)=cov(Ga)=E[(Ga)(Ga)T]=GE[a2]GT=G[σa2]GT=[σa2]GGT
among
G
=
[
1
2
Δ
t
2
1
2
Δ
t
2
Δ
t
Δ
t
]
T
G=\begin{bmatrix} {1\over2}\Delta t^2&{1\over2}\Delta t^2&\Delta t&\Delta t \end{bmatrix}^T
G=[21 Δ t221 Δ t2 Δ t Δ t]T . And for
σ
a
σ_a
σ a, empirical value can be taken
0.5
m
/
s
2
0.5m/s^2
0.5m/s2.
For the covariance matrix of measurement noise
R
R
R. It is related to the measurement vector. In this example, the measurable quantity is limited to the pedestrian speed in the x and y directions, that is, the measurement vector
z
z
z can be expressed as
z
=
[
v
x
v
y
]
T
z=\begin{bmatrix} v_x&v_y\end{bmatrix}^T
z=[vxvy]T. Covariance matrix of measurement noise
R
R
The elements on the diagonal of R reflect the variance of the error of each observation, while the elements on the non diagonal reflect the correlation between the errors of different observations. For velocity measurement, the measurements in the two directions are independent of each other, so the matrix
R
R
The non diagonal elements of R can be used separately because of 0
σ
v
x
σ_{v_x}
σ vx} and
σ
v
y
σ_{v_y}
σ vy is used to describe the deviation between the measured results and the actual values in the x and y directions of the sensor, which belongs to the inherent nature of the sensor and can be measured by consulting the data manual or conducting tests. Then, measure the noise covariance matrix
R
R
R can be written in the following matrix form:
R
=
[
σ
v
x
2
0
0
σ
v
y
2
]
R=\begin{bmatrix}σ_{v_x}^2&0\\0&σ_{v_y}^2\end{bmatrix}
R=[σvx200σvy2]
By discussing measurement vectors, we might as well discuss measurement matrices
H
H
H. In the measurement equation
z
k
=
H
k
x
k
+
ν
k
z_k=H_kx_k+ν_k
zk=Hkxk+ ν k +,
ν
ν
ν Is the measurement error,
z
k
z_k
zk # yes
m
×
1
m×1
m × 1-dimensional measurement vector,
x
k
x_k
xk is
n
×
1
n×1
n × 1-dimensional state vector. It can be seen that the measurement matrix
H
H
H is
m
×
n
m×n
m × n-dimensional matrix. Namely
H
H
Dimension of H and measurement vector
z
z
z. State vector
x
x
x is all about.
In the example, since only the velocities in the x and y directions can be measured, for simplicity, the z z z is written for [ v x v y ] T \begin{bmatrix} v_x&v_y\end{bmatrix}^T A 2 of [vx vy] T × 1-dimensional vector, due to the state vector x x x is 4 × One dimension, so the corresponding, H H H is [ 0 0 1 0 0 0 0 1 ] \begin{bmatrix}0&0&1&0\\0&0&0&1\end{bmatrix} 2 of [00 # 00 # 10 # 01] × 4-dimensional matrix. Similarly, if z z z is written as [ 0 0 v x v y ] T \begin{bmatrix}0&0&v_x&v_y\end{bmatrix}^T [0 # vx # vy] T, then H H H should be written as [ 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 ] \begin{bmatrix}0&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix} ⎣⎢⎢⎡0000000000100001⎦⎥⎥⎤. For more discussion on matrix dimension in Kalman filter process, please refer to [7].
P = np.diag([1000.0, 1000.0, 1000.0, 1000.0]) # P: For the prediction error covariance matrix, when it is uncertain, the diagonal takes an appropriate large value
print("------\nthe P is\n", P, P.shape)
H = np.matrix([[0.0, 0.0, 1.0, 0.0], # H: The measurement matrix can only measure the speed directly
[0.0, 0.0, 0.0, 1.0]])
print("------\nthe H is\n", H, H.shape)
ra = 0.09 # Measurement noise, random
R = np.matrix([[ra, 0.0], # R: Measurement noise covariance matrix
[0.0, ra]])
print("------\nthe R is\n", R, R.shape)
sv = 0.5 # As the pedestrian walking acceleration value of process noise, this is the empirical value
G = np.matrix([[0.5*dt**2],
[0.5*dt**2],
[dt],
[dt]])
Q = G*G.T*sv**2 # Q: Process noise covariance matrix
print("------\nthe Q is\n", Q, Q.shape)
Then, we need to randomly generate some measurement data for filtering algorithm.
# Randomly generate measurement data
measureNum = 200 # How many groups of measurement data are there in total
vx = 20 # Velocity in x direction
vy = 10 # Velocity in y direction
mx = np.array(vx + np.random.randn(measureNum)) # Generate random measurements in the x direction
my = np.array(vy + np.random.randn(measureNum)) # Generate random measurements in the y direction
measureData = np.vstack((mx, my))
print("measureData shape: ", measureData.shape)
print('Standard Deviation of Acceleration Measurements=%.2f \n You assumed %.2f in R' % (np.std(mx), R[0, 0]))
We can also plot the generated random data for viewing
fig = plt.figure(figsize=(16, 5))
plt.step(range(measureNum), mx, label= '$\dot x$')
plt.step(range(measureNum), my, label= '$\dot y$')
plt.ylabel(r'Velocity $m/s$')
plt.title('Measurements')
plt.legend(loc='best', prop={'size':18})
plt.show()
Finally, we use the previously defined variables to realize the calculation process of Kalman filter. The loop will continuously use the new measured values and the current state to calculate the state vector x x x to update.
for n in range(len(measureData[0])):
# Time update (Prediction)
# ======
# Project the state ahead
x = A*x
# Project the error covariance ahead
P = A*P*A.T + Q
# Measurement Update (Correction)
# ======
# Compute the Kalman Gain
_tempKpart = H*P*H.T + R
K = (P*H.T) * np.linalg.pinv(_tempKpart)
# Update the estimate via z
Z = measureData[:, n].reshape(2, 1)
_tempZpart = Z - (H * x)
x = x + (K * _tempZpart)
# Update the error covariance
P = (I - (K * H)) * P
1.2.3 - Code
The codes in this section and the previous section are mainly from the blog of Adam Shan [3]. Only some modifications have been made here to remove some codes that are easy to cause ambiguity, and the comments have been completed for reading.
import numpy as np
import matplotlib.pyplot as plt
# Initialization of Kalman filter parameters
x = np.matrix([[0.0, 0.0, 0.0, 0.0]]).T # X state matrix: x position, y position, X speed, y speed
print("the X is\n", x, x.shape)
P = np.diag([1000.0, 1000.0, 1000.0, 1000.0]) # P: For the prediction error covariance matrix, when it is uncertain, the diagonal takes an appropriate large value
print("------\nthe P is\n", P, P.shape)
dt = 0.1 # Time step between filter steps
A = np.matrix([[1.0, 0.0, dt, 0.0], # State transformation matrix (processing matrix) A
[0.0, 1.0, 0.0, dt],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0]])
print("------\nthe A is\n", A, A.shape)
H = np.matrix([[0.0, 0.0, 1.0, 0.0], # H: The measurement matrix can only measure the speed directly
[0.0, 0.0, 0.0, 1.0]])
print("------\nthe H is\n", H, H.shape)
ra = 0.09 # Measurement noise
R = np.matrix([[ra, 0.0], # R: Measurement noise covariance matrix
[0.0, ra]])
print("------\nthe R is\n", R, R.shape)
sv = 0.5 # As the pedestrian walking acceleration value of process noise, this is the empirical value
G = np.matrix([[0.5*dt**2],
[0.5*dt**2],
[dt],
[dt]])
Q = G*G.T*sv**2 # Q: Process noise covariance matrix
print("------\nthe Q is\n", Q, Q.shape)
I = np.eye(4)
print("------\nthe I is\n", I, I.shape)
# Randomly generate measurement data
measureNum = 200 # How many groups of measurement data are there in total
vx = 20 # Velocity in x direction
vy = 10 # Velocity in y direction
mx = np.array(vx + np.random.randn(measureNum)) # Generate random measurements in the x direction
my = np.array(vy + np.random.randn(measureNum)) # Generate random measurements in the y direction
measureData = np.vstack((mx, my))
print("measureData shape: ", measureData.shape)
print('Standard Deviation of Acceleration Measurements=%.2f \n You assumed %.2f in R' % (np.std(mx), R[0, 0]))
fig = plt.figure(figsize=(16, 5))
plt.step(range(measureNum), mx, label= '$\dot x$')
plt.step(range(measureNum), my, label= '$\dot y$')
plt.ylabel(r'Velocity $m/s$')
plt.title('Measurements')
plt.legend(loc='best', prop={'size':18})
plt.show()
# Process value saving
xt = []
yt = []
dxt= []
dyt= []
Zx = []
Zy = []
Px = []
Py = []
Pdx= []
Pdy= []
Rdx= []
Rdy= []
Kx = []
Ky = []
Kdx= []
Kdy= []
def SaveStates(x, Z, P, R, K): # x: State vector, Z: measured value, P: prediction error covariance matrix, R: measurement error covariance matrix, K: Kalman gain
xt.append(float(x[0]))
yt.append(float(x[1]))
dxt.append(float(x[2]))
dyt.append(float(x[3]))
Zx.append(float(Z[0]))
Zy.append(float(Z[1]))
Px.append(float(P[0, 0]))
Py.append(float(P[1, 1]))
Pdx.append(float(P[2, 2]))
Pdy.append(float(P[3, 3]))
Rdx.append(float(R[0, 0]))
Rdy.append(float(R[1, 1]))
Kx.append(float(K[0, 0]))
Ky.append(float(K[1, 0]))
Kdx.append(float(K[2, 0]))
Kdy.append(float(K[3, 0]))
for n in range(len(measureData[0])):
# Time update (Prediction)
# ======
# Project the state ahead
x = A*x
# Project the error covariance ahead
P = A*P*A.T + Q
# Measurement Update (Correction)
# ======
# Compute the Kalman Gain
_tempKpart = H*P*H.T + R
K = (P*H.T) * np.linalg.pinv(_tempKpart)
# Update the estimate via z
Z = measureData[:, n].reshape(2, 1)
_tempZpart = Z - (H * x)
x = x + (K * _tempZpart)
# Update the error covariance
P = (I - (K * H)) * P
# Save states (for plotting)
SaveStates(x, Z, P, R, K)
# Draw results
def PlotFilterResult():
_fig = plt.figure(figsize=(16, 9))
plt.step(range(len(measureData[0])), dxt, label='$filter Vx$')
plt.step(range(len(measureData[0])), dyt, label='$filter Vy$')
plt.step(range(len(measureData[0])), measureData[0], label='$measurement Vx$')
plt.step(range(len(measureData[0])), measureData[1], label='$measurement Vy$')
plt.axhline(vx, color='#999999', label='$true Vx$')
plt.axhline(vy, color='#999999', label='$true Vy$')
plt.xlabel('Filter Step')
plt.ylabel('Velocity')
plt.title("Estimate (Elements from State Vector $x$)")
plt.legend(loc='best', prop={'size': 11})
plt.ylim([0, 30])
def PlotEstimatePossition():
_fig = plt.figure(figsize=(16, 9))
plt.scatter(xt, yt, s=20, label='State', c='k') # Path segment
plt.scatter(xt[0], yt[0], s=100, label='Start', c='g') # starting point
plt.scatter(xt[-1], yt[-1], s=100, label='End', c='r') # End
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Position')
plt.legend(loc='best')
plt.axis('equal')
PlotEstimatePossition()
PlotFilterResult()
plt.show()