String matching is a common algorithm problem. There is a string to judge whether it contains another string.

For example, there is a string "aaaaabc" (main string). I want to know whether it contains another string "AAAB" (mode string)? Match the main string and pattern string.

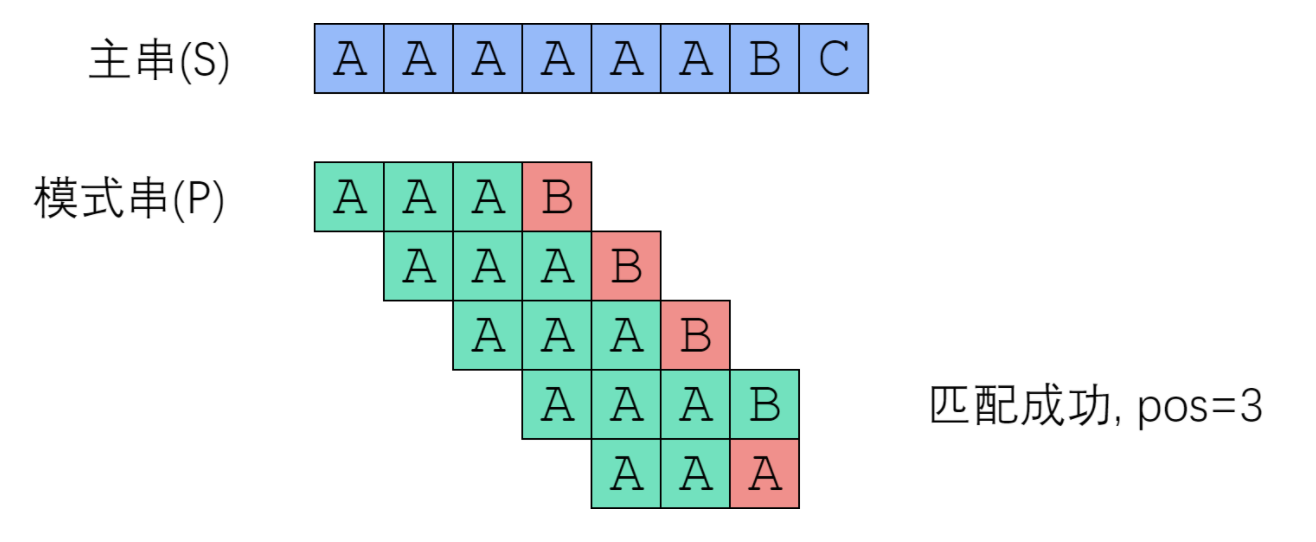
First, compare the first character of the string "aaaaabc" with the first character of the search term "AAAB".

AAAAAABC
AAAB

One character of the string is the same as the first character of the search term, and then compare the string with the next character of the search term. Until the string has one character, which is different from the corresponding character of the search term.

When the index of the string is 3, it is found that it is not equal. At this time, the most natural response is to move the search words back one bit as a whole, and then compare them one by one from the beginning.

AAAAAABC
 AAAB

Based on this idea, we can get the following program:

function bf(ts, ps) {
  let t = ts;
  let p = ps;
  let i = 0; // Position of main string
  let j = 0; // Position of the pattern string
  while (i < t.length && j < p.length) {
    if (t[i] === p[j]) { // When two strings are the same, the next one is compared
      i++;
      j++;
    } else {
      i = i - j + 1; // Once it doesn't match, i step back
      j = 0; // j returns to 0
    }
  }
  if (j === p.length) {
    return i - j
  } else {
    return -1;
  }
}

console.log(bf('AAAAAABC', 'AAAB'))

The above program is no problem, but it's not good enough! This is the solution complexity O(nm). It's too slow!

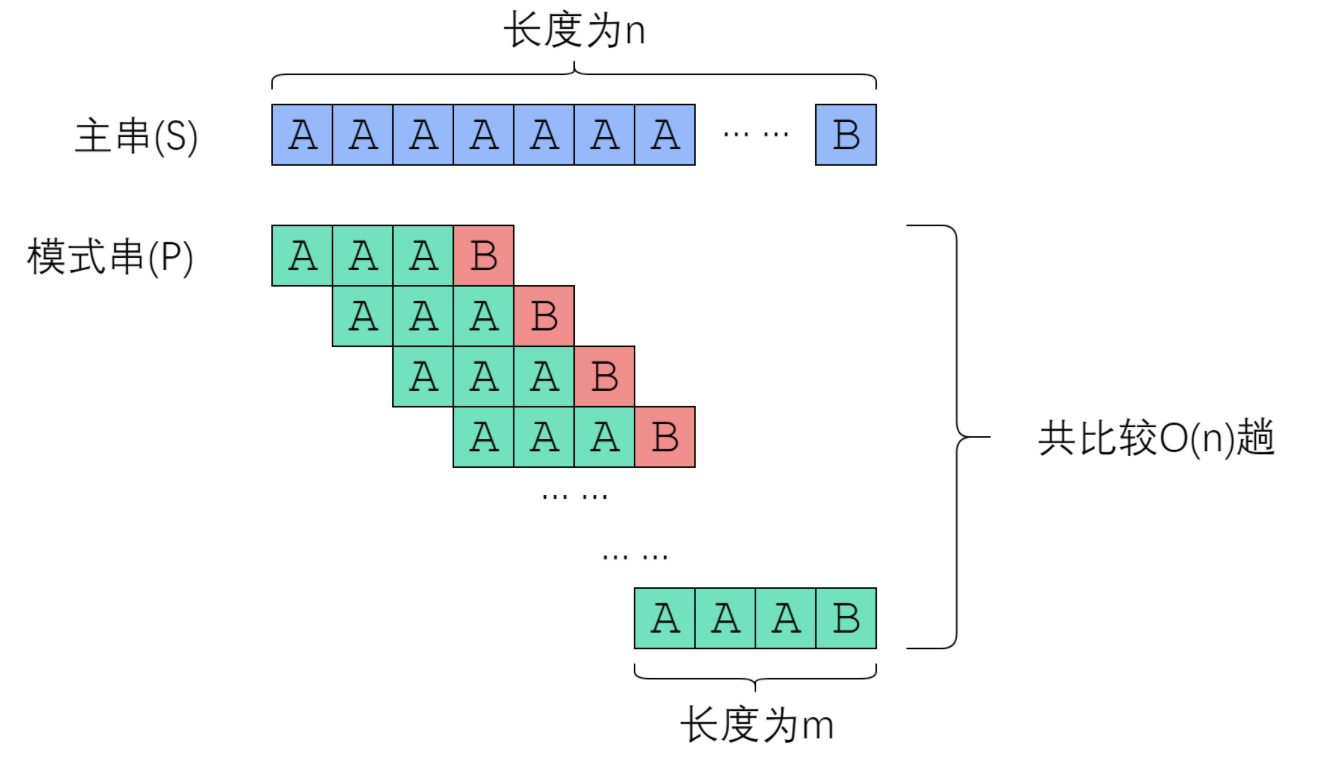
It's hard to reduce the complexity of string comparison (because comparing two strings can only compare characters one by one). Therefore, we consider reducing the number of comparison trips.

Skip string comparisons that are unlikely to succeed

Some string comparisons are likely to succeed; Some are impossible. If we skip string comparisons that will never succeed, we can hope that the complexity will be reduced to an acceptable range.

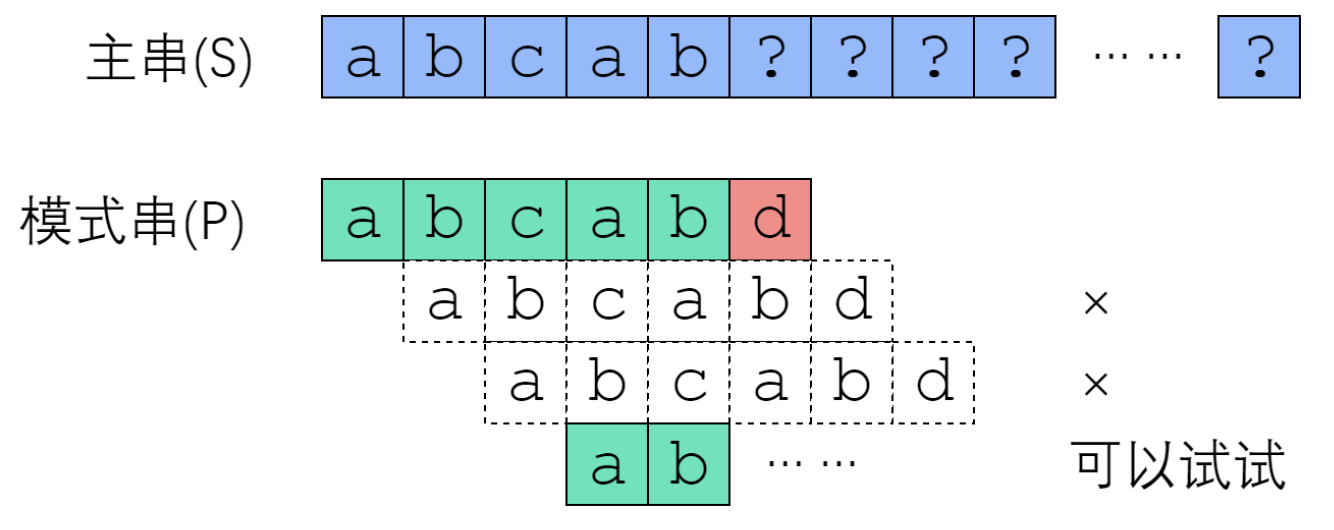
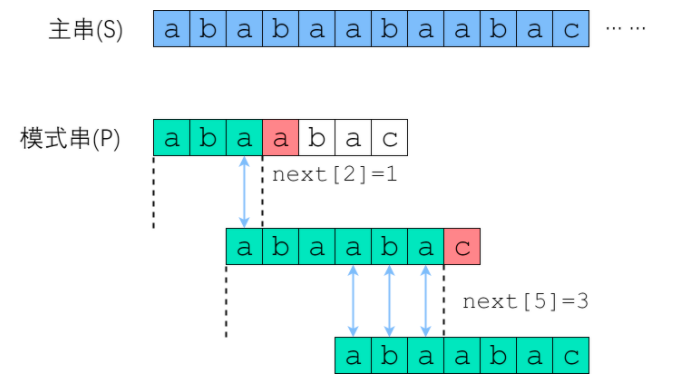
A basic fact is that when d doesn't match, you actually know that the first five characters are "abcab". If it is an artificial search, i will not be moved to index 1, but we will directly move to index 3! You can come to the second "ab" position.

Therefore, the key point of the whole KMP is that when a character does not match the main string, we should know where to move the pointer?

Moving digit = Number of characters matched - Corresponding partial matching value

First, we need to understand two concepts: "prefix" and "suffix". "Prefix" refers to the combination of all headers of a string except the last character; "Suffix" refers to the combination of all tails of a string except the first character.

The prefix of "abcab" is [a, ab, abc, abca], the suffix is [bcab, cab, ab, b], the common element is "ab", and the length is 2;

The essence of "partial match" is that sometimes there will be repetition at the beginning and end of the string. For example, if there are two "ab" in "abcab", then its "partial matching value" is 2 (the length of "ab"). When the search term moves, the first "ab" moves backward to the index of 3 (string length 5 - partial matching value 2), and you can come to the position of the second "ab".

function getNext(p) {
  let nxt = [];
  nxt.push(0); // next[0] must be 0
  let x = 1; // So nxt[1] start to find
  let now = 0;
  while (x < p.length) {
    if (p[now] === p[x]) { // If p[now] == p[x], one bit can be extended to the right
      now += 1
      x += 1
      nxt.push(now)
    } else if (now) {
      now = nxt[now - 1] // Reduce now to nxt[now - 1]
    } else {
      nxt.push(0) // now is 0 and cannot be reduced any more, so nxt[x] = 0
      x += 1
    }
  }
  return nxt
}

console.log(getNext('abcab'))
// [ 0, 0, 0, 1, 2 ]

Move the ruler according to nxt array.

function bf(ts, ps) {
  let t = ts;
  let p = ps;
  let i = 0; // Position of main string
  let j = 0; // Position of the pattern string
  let nxt = getNext(ps)
  while (i < t.length && j < p.length) {
    if (t[i] === p[j]) { // When two strings are the same, the next one is compared
      i++;
      j++;
    } else {
      // It's a mismatch
      if (j) {
        j = nxt[j - 1] // Move ruler according to nxt array
      } else {
        i++; // ps[0] is mismatched. Move the ruler one bit to the right
      }
    }
  }
  if (j === p.length) {
    return i - j
  } else {
    return -1;
  }
}