1, 01 knapsack problem
each item can only be selected or not, and each item can only be selected once
Topic overview:
title link: 01 knapsack problem
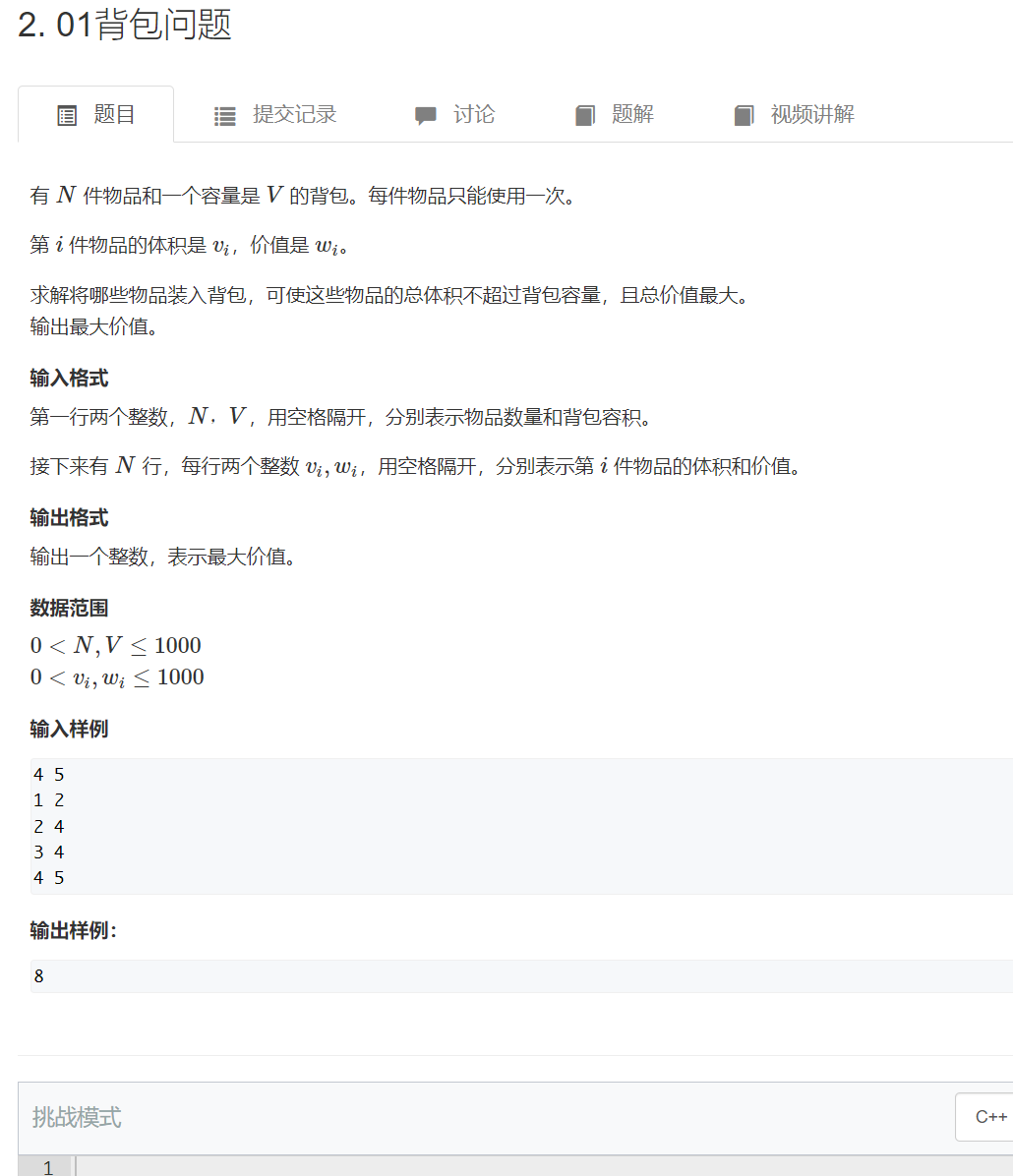
Solution:
f(i,j) represents the maximum value when only the first i items are viewed and the total volume is j. Our answer is max{f(n,k),k=0~v}
1 do not select the i-th item, at this time, f(i,j)=f(i-1,j);
2 select the i-th item, where f(i,j) = f(i-1,j-v[i])+w[i];
f(i,j)=max{1.,2.};, Initial condition f(0,0) = 0// If none is selected, the volume is 0, so the value is 0
time complexity: the state is N*V and the state transition is O(1), so the time complexity is O(N*V). Look at the data range, N*V=1000000. Compared with the following table, our algorithm is sufficient:

space complexity sizeof(int)*N*V=4*1000000 bit, about 4MB. C / C + + is generally 64MB, which is completely ok. C + + can measure 107 ~ 108 times in a second, which is also ok.
the knapsack problem satisfies the optimal substructure, so dynamic programming can be used. It is proved as follows:
Back
package
ask
topic
can
with
surface
show
by
:
m
a
x
(
∑
i
=
1
N
w
i
x
i
)
s
.
t
.
∑
i
=
1
N
v
i
x
i
<
=
V
set up
y
1
,
y
2
,
.
.
.
,
y
n
yes
primary
ask
topic
of
most
excellent
solution
,
that
Do you
y
1
,
y
2
,
.
.
.
,
y
n
−
1
have to
however
yes
son
ask
topic
m
a
x
(
∑
i
=
1
N
−
1
w
i
x
i
)
s
.
t
.
∑
i
=
1
N
−
1
v
i
x
i
<
=
V
−
w
N
y
N
card
bright
:
Gather
use
back
card
method
,
set up
Save
stay
one
group
solution
z
1
,
z
2
,
.
.
.
,
z
N
−
1
yes
upper
noodles
son
ask
topic
of
most
excellent
solution
that
Do you
∑
i
=
1
N
−
1
w
i
z
i
>
=
∑
i
=
1
N
−
1
w
i
y
i
And
∑
i
=
1
N
−
1
v
i
z
i
<
=
V
−
w
N
y
N
that
Do you
hair
present
∑
i
=
1
N
−
1
w
i
z
i
+
w
N
y
N
>
=
∑
i
=
1
N
w
i
y
i
And
∑
i
=
1
N
−
1
v
i
z
i
+
w
N
y
N
<
=
V
this
no
Just
say
bright
z
1
,
z
2
,
.
.
.
,
z
N
−
1
,
y
N
just
yes
primary
ask
topic
of
most
excellent
solution
Well
,
this
And
topic
meaning
spear
shield
place
with
primary
ask
topic
have to
card
bright
.
Knapsack problem can be expressed as: \ \ max (\ sum {I = 1} ^ {n} {w_ix_i}) \ \ S.T. \ sum_ {I = 1} ^ {n} {v_ix_i} < = V \ \ set y_1,y_2,...,y_n is the optimal solution of the original problem, then y_1,y_2,...,y_{n-1} must be a sub problem \ \ max (\ sum {I = 1} ^ {n-1} {w_ix_i}) \ \ S.T. \ sum_ {i=1}^{N-1}{v_ix_i}<=V-w_ Ny_ N \ \ prove that there is a set of solutions Z by using the counter proof method_ 1,z_ 2,..., z_ {n-1} is the optimal solution of the above subproblem \ \ then \ sum_ {i=1}^{N-1}{w_iz_i}>=\sum_ {I = 1} ^ {n-1} {w_iy_i} and \ sum_ {i=1}^{N-1}{v_iz_i}<=V-w_ Ny_ N \ \ then find \ sum_ {i=1}^{N-1}{w_iz_i}+w_ Ny_ N>=\sum_ {I = 1} ^ {n} {w_iy_i} and \ sum_ {i=1}^{N-1}{v_iz_i}+w_ Ny_ N < = V \ \ doesn't that mean z_1,z_2,...,z_{N-1},y_N is the optimal solution of the original problem, which contradicts the meaning of the question \ \ so the original problem has to be proved.
The knapsack problem can be expressed as: max(i=1 Σ N wi xi) s.t.i=1 Σ N vi xi < = V let y1, y2, yN is the optimal solution of the original problem, then y1, y2, yN − 1 must be the subproblem max(i=1 ∑ N − 1 wi xi) s.t.i=1 ∑ N − 1 vi xi < = V − wN yN. It is proved that there is a set of solutions z1, z2, If zN − 1 is the optimal solution of the above subproblem, then i=1 ∑ N − 1 wi zi > = i=1 ∑ N − 1 wi yi and i=1 ∑ N − 1 vi zi < = V − wN yN. Then i=1 ∑ N − 1 wi zi + wN yN > = i=1 ∑ N wi yi and i=1 ∑ N − 1 vi zi + wN yN < = V. This does not mean that z1, z2, zN − 1, yN is the optimal solution of the original problem, which is contradictory to the meaning of the question, so the original problem has to be proved.
therefore, the substructure of this problem is optimal, and dynamic programming can be used. The code is as follows:
#include <iostream>
#include <vector>
using namespace std;
#define NUM 1001
int main()
{
int N;
int V;
cin >> N >> V;
//dp[i][j] indicates the maximum value of the first I items only when the subscript is selected or not, and the volume is j
//Consider the ith item, or don't choose it. At this time, the value is equal to dp[i - 1][j]
//If you choose it, the value is dp[i - 1][j - v[i]] + w[i]
//dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]] + w[i])
//dp[0][0] = 0;
vector<vector<int>> dp(N + 1,vector<int>(V + 1));
//At the beginning, the default full initialization is 0, which also shows that it is a reasonable reason not to put anything
int v[NUM], w[NUM];
//v[i] represents the volume of the ith article
//w[i] indicates the value of the ith item
for (int i = 1; i <= N; ++i)
{
cin >> v[i] >> w[i];
}
for (int i = 1; i <= N; ++i)
{
for (int j = 0; j <= V; ++j)
{
dp[i][j] = dp[i - 1][j];
if (j - v[i] >= 0)
{
dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
}
}
int ret = 0;
for (int j = 0; j <= V; ++j)
{
ret = max(ret, dp[N][j]);
}
cout << ret << endl;
return 0;
}
Optimization:
note that this problem can be optimized with rolling array as follows:
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int N,V;
cin >> N >> V;
vector<int> v(N + 1);
vector<int> w(N + 1);
for (int i = 1; i <= N; ++i)
{
//v[i] represents the volume of the ith article
//w[i] represents the price of the ith item
cin >> v[i] >> w[i];
}
//Observe the state transition equation:
//f(i,j) = max(f(i-1,j), f(i-1,j-v[i]) + w[i])
//Only related to the previous line
//You can optimize with a rolling array
vector<int> dp(V + 1);
for (int i = 1; i <= N; ++i)
{
//We notice that the state of the last line we want is f(i-1,j) and f(i-1, j - v[i])
//The previous one is good to say that it must have been calculated in f[j] through forward traversal
//However, if the normal 0~j traversal is performed, f(i - 1, j - v[i]) must be updated
//So we're going to turn the inner loop in the opposite direction
//In this way, f(i-1,j-v[i]) must have not been updated. It is in the I-1 of the upper layer
//And ensure that j-v[i] is greater than 0
for (int j = V; j >= v[i]; --j)
{
dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
}
}
//dp[V] must be the optimal solution, because the optimal solution will be transferred to the last layer by layer
cout << dp[V] << endl;
return 0;
}
Just fill the backpack with volume V:
the state transition equation is consistent, so only the initial conditions need to be modified;
just full, to be initialized to DP [i] [j] = int_ Min (f[j]) for one bit array; (if it is the minimum utility, it is initialized to INT_MAX). This shows that there is no reasonable solution when the knapsack with volume j is just filled at the beginning, but dp[i][0] still needs to be given 0, indicating that the maximum value of the knapsack with volume 0 is 0. Finally, when outputting, if dp[N][V]==INT_MIN, indicating that there is no understanding of the problem, and the output has no solution.
practice:
LeetCode416. Split equal sum subset
Solution:
class Solution {
public:
bool canPartition(vector<int>& nums)
{
int sum = 0;
int maxelem = INT_MIN;
for (auto e : nums)
{
maxelem = max(maxelem, e);
sum += e;
}
if (sum % 2 != 0)
{
return false;
}
/*
Can you fill a backpack with a volume of sum/2
f[i][j]It is defined as true when items with subscript 0~i can just fill the backpack with volume j
false when the backpack with volume j cannot be filled exactly
For the element nums[i] with subscript i, there are two cases
If num [i] < = J, you can choose this item or not
If you choose this item, the subproblem is to consider that the elements of 0~i-1 subscript are just filled with the volume of j-nums[i]
I.e. F - nums [i] [1]
If you don't choose this item, the sub problem is f[i-1][j]
As long as one of them is true, then f[i][j] it is true
So if nums [i] < = J
f[i][j] = f[i - 1][j] || f[i - 1][j - nums[i]]
What if nums [i] < J
You can't select the element with subscript i
Then f[i][j] = f[i - 1][j]
Considering the initial value f[i][0], it's certainly OK to fill the backpack with volume 0. Just don't choose it
So f[i][0] = true;
*/
int N = nums.size();
if (N < 2)
{
return false;
}
int V = sum / 2;
if (V < maxelem)
{
return false;
}
vector<vector<bool>> f(N, vector<bool>(V + 1));
for (int i = 0; i < N; ++i)
{
f[i][0] = true;
}
f[0][nums[0]] = true;
for (int i = 1; i < N; ++i)
{
for (int j = 0; j <= V; ++j)
{
if (nums[i] <= j)
{
f[i][j] = f[i - 1][j] || f[i - 1][j - nums[i]];
}
else
{
f[i][j] = f[i - 1][j];
}
}
}
return f[N - 1][V];
}
};
Optimization:
class Solution {
public:
bool canPartition(vector<int>& nums)
{
int N = nums.size();
int maxelem = INT_MIN;
int sum = 0;
for (auto e : nums)
{
sum += e;
if (maxelem < e)
{
maxelem = e;
}
}
//If sum is an odd number, it must not be divided into equal sum subsets
if (sum & 1 != 0)
{
return false;
}
int V = sum / 2;
//If the largest element is larger than the backpack we want to fill
//It can't be divided into two equal sum subsets
if (V < maxelem)
{
return false;
}
//Into a backpack just filled with a volume of V
/*
f[i][j] = f[i - 1][j] || f[i - 1][j - nums[i]]
*/
vector<bool> f(V + 1);
f[0] = true;
f[nums[0]] = true;
for (int i = 1; i < N; ++i)
{
for (int j = V; j >= 1; --j)
{
if (j - nums[i] >= 0)
{
//The purpose of traversing from a large number is to ensure that f[j - nums[i]] is the f[i - 1][j - nums[i]] calculated in the previous round
f[j] = f[j] || f[j - nums[i]];
}
}
}
return f[V];
}
};
2, Complete knapsack problem
Topic overview:
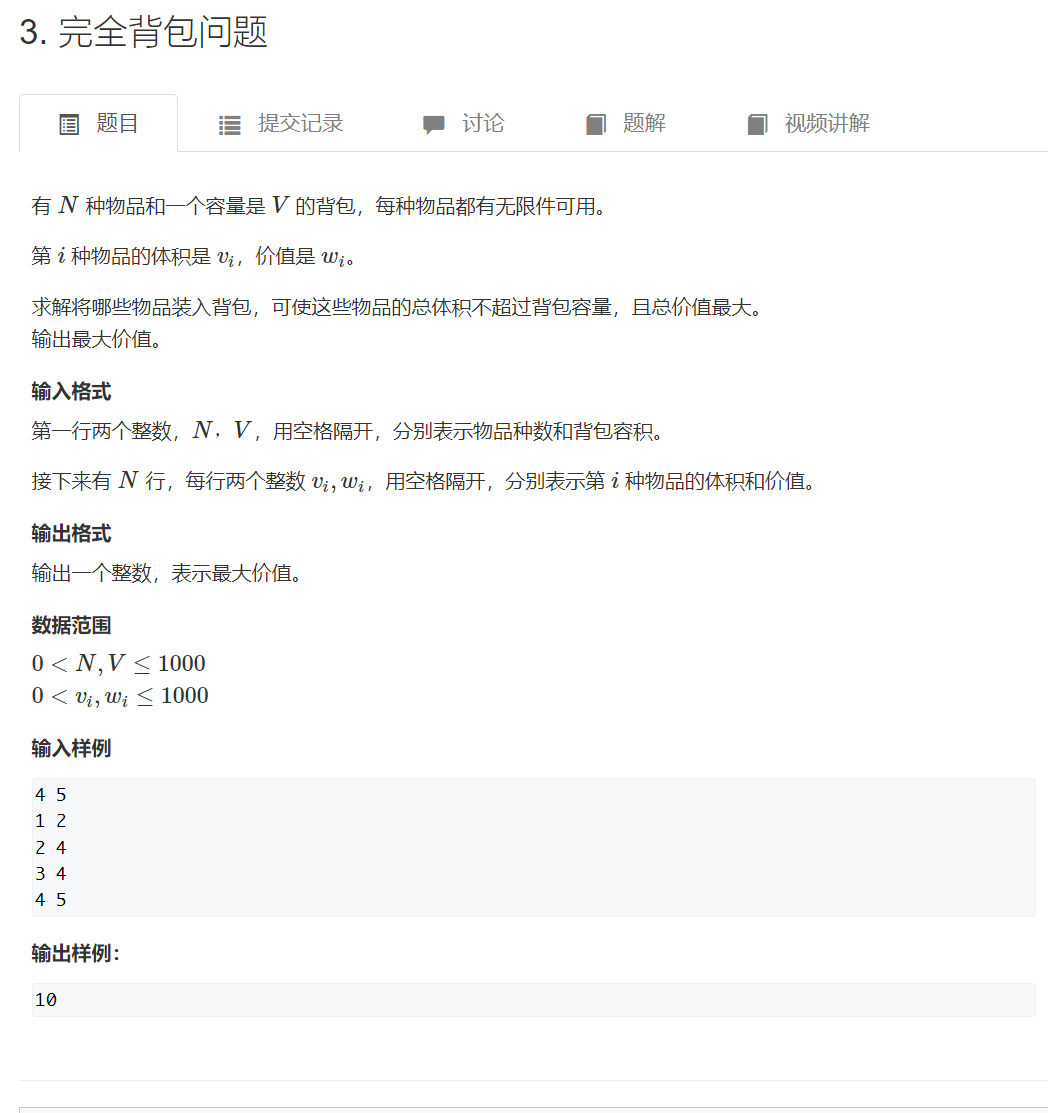
Title Link: Complete knapsack problem
Solution:
define the state f(i,j) only considering the maximum value when the first I represents the total volume does not exceed j. think carefully, this is the complete knapsack problem, so when the state transition, we can consider not selecting the value of the i-th article, or selecting one i-th article, two i-th articles... Selecting K i-th article (k * w [i] < = j), so the state transition equation should be as follows:
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
)
,
f
(
i
−
1
,
j
−
v
[
i
]
)
+
w
[
i
]
,
f
(
i
−
1
,
j
−
2
∗
v
[
i
]
)
+
2
∗
w
[
i
]
,
.
.
.
,
f
(
i
−
1
,
j
−
k
∗
v
[
i
]
)
+
k
∗
w
[
i
]
)
,
s
.
t
.
j
−
k
∗
v
[
i
]
>
=
0
f(i,j) = max(f(i-1,j),f(i-1,j-v[i])+w[i],f(i-1,j-2*v[i])+2*w[i],...,f(i-1,j-k*v[i])+k*w[i]),\\ s.t.j-k*v[i]>=0\\
f(i,j)=max(f(i−1,j),f(i−1,j−v[i])+w[i],f(i−1,j−2∗v[i])+2∗w[i],...,f(i−1,j−k∗v[i])+k∗w[i]),s.t.j−k∗v[i]>=0
the simple code to realize this state escape equation should be:
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int N,V;
cin >> N >> V;
vector<int> v(N + 1);
vector<int> w(N + 1);
for (int i = 1; i <= N; ++i)
{
cin >> v[i] >> w[i];
}
vector<vector<int>> f(N + 1, vector<int>(V + 1));
/*
Don't choose the i-th item, choose 1 i-th item, choose 2 i-th items
f(i,j) = max(f(i-1,j),f(i-1,j-v[i])+w[i],f(i-1,j-2*v[i])+2*w[i],...,f(i-1,j-k*v[i])+k*w[i]),
s.t.k = 1,2,3,4,...j-k*v[i]>=0
*/
for (int i = 1; i <= N; ++i)
{
for (int j = 0; j <= V; ++j)
{
for (int k = 0; k * v[i] <= j; ++k)
{
//Here, when k equals 0, f[i - 1][j] is included
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
cout << f[N][V] << endl;
return 0;
}
run it and find:
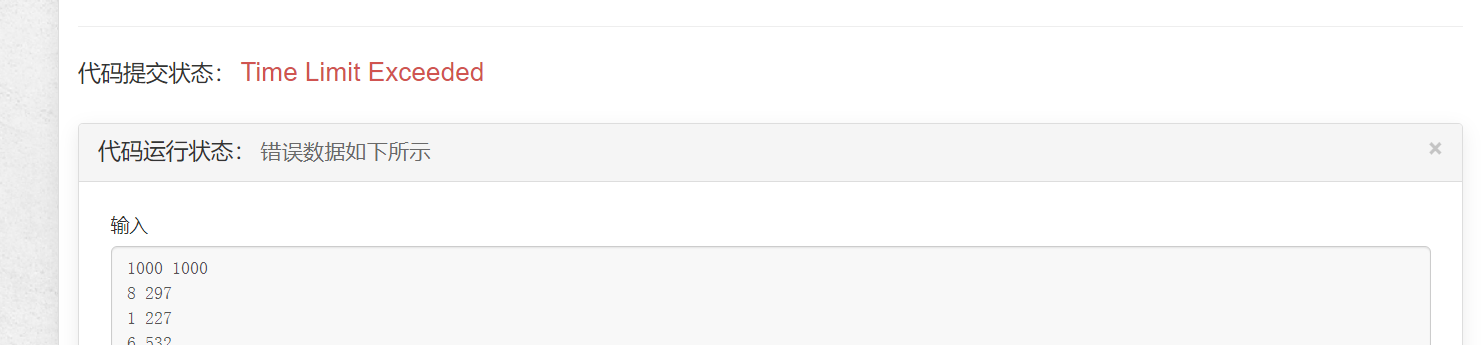
because our time complexity exceeds O(N*V), the time complexity becomes O(N*V*V) Find ways to optimize.
note:
f
(
i
,
j
−
v
[
i
]
)
=
m
a
x
(
f
(
i
−
1
,
j
−
v
[
i
]
)
,
f
(
i
−
1
,
j
−
2
∗
v
[
i
]
)
+
1
∗
w
[
i
]
,
.
.
.
f
(
i
−
1
,
j
−
k
∗
v
[
i
]
)
+
(
k
−
1
)
∗
w
[
i
]
)
s
.
t
.
k
=
1
,
2
,
3
,
.
.
.
j
−
k
∗
w
[
i
]
>
=
0
f(i,j-v[i]) = max(f(i-1,j-v[i]),f(i-1,j-2*v[i])+1*w[i],...f(i-1,j-k*v[i])+(k-1)*w[i])\\ s.t.k = 1,2,3,...j-k*w[i]>=0\\
f(i,j−v[i])=max(f(i−1,j−v[i]),f(i−1,j−2∗v[i])+1∗w[i],...f(i−1,j−k∗v[i])+(k−1)∗w[i])s.t.k=1,2,3,...j−k∗w[i]>=0
compare with the original state escape equation:
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
)
,
f
(
i
−
1
,
j
−
v
[
i
]
)
+
w
[
i
]
,
f
(
i
−
1
,
j
−
2
∗
v
[
i
]
)
+
2
∗
w
[
i
]
,
.
.
.
,
f
(
i
−
1
,
j
−
k
∗
v
[
i
]
)
+
k
∗
w
[
i
]
)
,
s
.
t
.
j
−
k
∗
v
[
i
]
>
=
0
f(i,j) = max(f(i-1,j),f(i-1,j-v[i])+w[i],f(i-1,j-2*v[i])+2*w[i],...,f(i-1,j-k*v[i])+k*w[i]),\\ s.t.j-k*v[i]>=0\\
f(i,j)=max(f(i−1,j),f(i−1,j−v[i])+w[i],f(i−1,j−2∗v[i])+2∗w[i],...,f(i−1,j−k∗v[i])+k∗w[i]),s.t.j−k∗v[i]>=0
it is found that the two formulas can be combined as follows:
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
)
,
f
(
i
,
j
−
v
[
i
]
)
+
w
[
i
]
)
f(i,j)=max(f(i-1,j),f(i,j-v[i])+w[i])
f(i,j)=max(f(i−1,j),f(i,j−v[i])+w[i])
we get a new state transition equation! The operation of this equation transfer is obviously O(1), so the time complexity is optimized to O(N*V);
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int N, V;
cin >> N >> V;
vector<int> v(N + 1);
vector<int> w(N + 1);
for (int i = 1; i <= N; ++i)
{
cin >> v[i] >> w[i];
}
vector<vector<int>> f(N + 1, vector<int>(V + 1));
/*
The state transition equation we derived:
f(i,j) = max(f(i - 1,j),f(i,j-v[i]) + w[i])
*/
for (int i = 1; i <= N; ++i)
{
for (int j = 0; j <= V; ++j)
{
f[i][j] = f[i - 1][j];
if (j - v[i] >= 0)
{
f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
}
}
cout << f[N][V] << endl;
return 0;
}
Optimization:
similarly, use the rolling array to optimize the space complexity to O(V) It should be noted here that in the state transition equation:
f
(
i
,
j
)
=
m
a
x
(
f
(
i
−
1
,
j
)
,
f
(
i
,
j
−
v
[
i
]
)
+
w
[
i
]
)
f(i,j) = max(f(i - 1,j),f(i,j-v[i]) + w[i])
f(i,j)=max(f(i−1,j),f(i,j−v[i])+w[i])
the last one starts with i, so it must be the data calculated by the bank, so the inner loop should be calculated from small to large, rather than from large to small like the 0-1 knapsack problem.
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int N, V;
cin >> N >> V;
vector<int> f(V + 1);
int v, w;
for (int i = 1; i <= N; ++i)
{
/*
Because the inner circulation is fixed, i is a fixed object
So you can put in the process of inputting v[i] w[i]
*/
cin >> v >> w;
for (int j = 0; j <= V; ++j)
{
/*
If j < v[i], it means that v[i] cannot be filled when the space is j
If you can't plug it, you don't have to let f[j] keep the data calculated in the last round, that is, f(i - 1,j)
*/
if (j >= v)
{
f[j] = max(f[j], f[j - v] + w);
}
}
}
cout << f[V] << endl;
return 0;
}
Just fill the backpack with volume V:
if the question is about a knapsack just filled with V volume, it is first found that the state transition equation is consistent, then only the initial conditions need to be modified.
then when initializing, just set f(m) two-dimensional array as f [i] [J], m= 0 initialized to INT_MIN (if it is the minimum utility, initialize it to INT_MAX), indicating that it is not understood at the beginning. However, f(0) still needs to be initialized to 0, because the maximum utility of the backpack composed of 0 volume is really 0, so it can't hold things. The final output is, pay attention to check whether f(V) is equal to INT_MIN to check whether there is understanding.
practice:
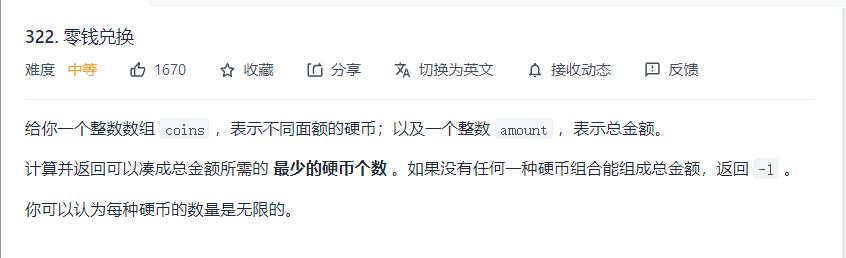
Solution:
this problem can be regarded as a variant of the complete knapsack problem. The volume of the ith item is coins[i - 1], and the value is 1. It just fills a knapsack with a volume of amount, and the minimum value required.
define f(i,j) as the minimum value required for the first i elements to fill the backpack with space j, obviously f(i,0) = 0;, All others are initialized to INT_MAX indicates that there is no legal solution at this time.
the state transition equation of the complete knapsack problem with value 1 is:
f
(
i
,
j
)
=
m
i
n
(
f
(
i
−
1
,
j
)
,
f
(
i
,
j
−
c
o
i
n
s
[
i
−
1
]
)
+
1
)
f(i,j) = min(f(i-1,j), f(i,j-coins[i-1])+1)
f(i,j)=min(f(i−1,j),f(i,j−coins[i−1])+1)
so the code is as follows:
class Solution {
public:
int coinChange(vector<int>& coins, int amount)
{
/*
It is transformed into a complete knapsack problem
The value of each coin is 1, and the volume of each coin is coins[i]
The goal is the minimum value used to fill the volume of amount exactly
f[i][j] is defined as the minimum value used to consider that the first I elements just fill the backpack with volume j
f[i][j] = min(f[i - 1][j], f[i][j - coins[i]] + 1)
f[0][0] = 0
*/
int size = coins.size();
vector<vector<int>> dp(size + 1, vector<int>(amount + 1, INT_MAX));
for (int i = 0; i <= size; ++i)
{
dp[i][0] = 0;
}
for (int i = 1; i <= size; ++i)
{
for (int j = 1; j <= amount; ++j)
{
dp[i][j] = dp[i - 1][j];
if (j - coins[i - 1] >= 0)
{
/*
Written as dp[i][j] = min(dp[i-1][j], dp[i][j - coins[i - 1]] + 1)
Maybe because DP [i] [J - Coins [I - 1]] = int_ Overflow due to Max
So put it another way
*/
if (dp[i][j] - 1 > dp[i][j - coins[i - 1]])
{
dp[i][j] = dp[i][j - coins[i - 1]] + 1;
}
}
}
}
//If dp[size][amount] == INT_MAX indicates that there is no legal solution and returns - 1
return dp[size][amount] == INT_MAX ? -1 : dp[size][amount];
}
};
optimize space complexity:
class Solution {
public:
int coinChange(vector<int>& coins, int amount)
{
/*
The value of each item is 1 and the volume is coins[i - 1]
The minimum value required to fill the volume of amount exactly
State transition equation
f[i][j] = min(f[i - 1][j], f[i][j - coins[i - 1]] + 1)
*/
int size = coins.size();
vector<int> dp(amount + 1, INT_MAX);
/*
dp[j]It is the minimum value required for the first i elements in the current round to form the backpack with volume j
For the sake of punishment, if it cannot be formed, the minimum value is INT_MAX
*/
dp[0] = 0;//The backpack with a composition volume of 0 can obviously be composed without any coins
for (int i = 1; i <= size; ++i)
{
for (int j = coins[i - 1]; j <= amount; ++j)
{
/*
dp[j] = min(dp[j], dp[j - coins[i - 1]] + 1);
Int will occur if it is written like this_ Overflow of MAX + 1
So write the following equivalent version
*/
if (dp[j] - 1 > dp[j - coins[i - 1]])
{
dp[j] = dp[j - coins[i - 1]] + 1;
}
}
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}
};
In short, if the knapsack equation is completely changed to the knapsack equation, note that the difference between the knapsack equation and the knapsack equation is completely changed.
3, Multiple knapsack problem
Topic overview:

Link: Multiple knapsack problem 1
Analysis: the data range is 100. We can solve it with O(N^3) algorithm. Obviously, this problem is a simplified version of the complete knapsack problem. Don't simplify it according to the state transition equation of the complete knapsack problem. Choose 0 I, 1 I, 2 I,..., and K is t.k*v[i] <= j && k <= w[i].
Pure violence algorithm solution:
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int N, V;
cin >> N >> V;
vector<int> v(N + 1);//Volume of the ith Article v[i]
vector<int> w(N + 1);//Value of the ith item w[i]
vector<int> s(N + 1);//Maximum number of choices for the ith item s[i]
for (int i = 1; i <= N; ++i)
{
cin >> v[i] >> w[i] >> s[i];
}
vector<vector<int>> dp(N + 1, vector<int>(V + 1));
/*
State transition equation for the ith item, you can choose not to put one or two... To put s[i] one
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - k * v[i]] + k * w[i]);
k <= s[i] And K * V [i] < = J
*/
for (int i = 1; i <= N; ++i)
{
for (int j = 0; j <= V; ++j)
{
for (int k = 0; k * v[i] <= j && k <= s[i]; ++k)
{
dp[i][j] = max(dp[i][j], dp[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
cout << dp[N][V] << endl;
return 0;
}
Space complexity Optimization:
similarly, this dynamic programming state transition equation can be optimized by reverse traversal of rolling array:
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int N, V;
cin >> N >> V;
int v, w, s;
vector<int> dp(V + 1);
for (int i = 1; i <= N; ++i)
{
cin >> v >> w >> s;
for (int j = V; j >= 0; --j)
{
for (int k = 1; k * v <= j && k <= s; ++k)
{
/*
f[i][j] = max(f[i - 1][j], f[i - 1][j - k * v[i]] + k * w[i])
k <= s[i] && k * v[i] <= j
*/
dp[j] = max(dp[j], dp[j - k * v] + k * w);
}
}
}
cout << dp[V] << endl;
return 0;
}
Time complexity: O(N * V * V/w)
Space complexity: O(V)
Time complexity optimization 1: binary optimization method

the data range of this problem has been expanded to 1000 and 2000. If we use the O (nvv / W) algorithm, the number of operations will reach 10 ^ 9, which will be exceeded.
when considering how to simplify this multiple knapsack problem into a 0-1 knapsack problem, the first thought is that each item can be selected s[i]. Then I disassemble each item, which will become a 0-1 knapsack problem of selection and non selection, but the time complexity will also exceed. The problem s[i] < = 20002000 * 2000 * 1000 is at the level of 10 ^ 9.
a more concise disassembly method is the binary disassembly method, such as 7. It is required to disassemble into a minimum number of numbers less than 7, so that all numbers less than 7 can be combined by these numbers.
0 ~ 7 has 8 schemes. The binary consideration method is adopted. 0, 0 and 0. The three positions can be filled with 1 or not respectively. In this way, it can be transformed into 1, 2 and 4. In this way, the three numbers can express the 8 schemes.
transform this problem. How many numbers can a number with size s be divided into at least so that these numbers can express all numbers from 0 to s?
the answer is [log2s] + 1. Take 10 as an example. 10 actually needs four numbers, but 1, 2, 4, 8 can express numbers from 0 to 15. Obviously, the expression range is too wide, so in fact, the last number can be reduced until the sum of these four numbers is 10,1, 2, 4, 3
why can all numbers from 0 to 10 be expressed in this way? First of all, if we choose 1, 2, 4, the number we can represent is 07, and if we add a number 3, the number we can represent is 010.
so gather s and select those numbers of log2s. The last number becomes s-1-2-4-8 -.... the range of the previous number is 0~2^([log2s]), and then add the last number to represent all numbers of 0~s. because the sum has just reached s, it will not overflow.
bring this idea into the process of transforming into 0-1 backpack. For each item, the split is not s, but the level of log2s
measure the time complexity. 1000 * 2000 * log2 2000 = 2000 000 * 11 is 2kw.
so we have to make each item according to 1 2 4 8... Split, and then transform it into 0 - 1 knapsack problem. The code is as follows:
#include <iostream>
#include <vector>
using namespace std;
/*
Define a good structure, and each good is used to undertake the divided goods
*/
struct good
{
int v;
int w;
};
int main()
{
int N, V;
cin >> N >> V;
vector<good> goods;
int v, w, s;
/*
The following paragraph is to bring in each type of goods, and the value of each volume v is w
Select s at most
Then according to the binary segmentation method, it is packaged into one item, two items and four items
*/
for (int i = 0; i < N ; ++i)
{
cin >> v >> w >> s;
for (int k = 1; k <= s; k *= 2)
{
s -= k;
goods.push_back({v * k, w * k});
}
/*
If there is any remaining, pack the remaining directly into one copy according to the binary segmentation method
*/
if (s > 0)
{
goods.push_back({v * s, w * s});
}
}
vector<int> f(V + 1);
/*
The following is a knapsack problem. The number is the number in the goods array
Value is the goods [i] in that structure v goods[i]. w
So the traversal of the structure is put outside
Using the scope of C++11 for
*/
for (auto e : goods)
{
for (int j = V; j >= e.v; --j)
{
f[j] = max(f[j], f[j - e.v] + e.w);
}
}
cout << f[V] << endl;
return 0;
}
The time complexity is optimized to O(N*logs*V);
however, it can also be optimized:
Time complexity optimization 2: monotone queue optimization method

if the data range at this time still uses the just algorithm, 1000* log(20000) * 20000 = 1000 * 20000 * 14 = 3 * 10^8, it is close to the upper limit. It is likely that it will fail.
we hope to optimize this problem to O(N*V)
4, Hybrid knapsack problem
5, Knapsack problem with two-dimensional cost
6, Grouping knapsack problem
divided into many groups, each group can only choose one, and the items in the group are mutually exclusive.
7, Solution number of knapsack problem
8, Solution to knapsack problem
9, Knapsack problem with dependency
to select an item, you must select its dependent items.
reference
- Backpack problem 9 lecture topic
- Meow programming lesson 3: dynamic programming 01 Backpack
- ACWing 3. Complete knapsack problem by Charles
- The complexity of the inverse calculation method from the data range and the content of the algorithm author yxc
- SMON, author of knapsack problem series of dynamic programming
- dd Daniel's backpack 9