catalogue

1. Basic definitions

2. Algorithm principle

2.1 advantages and disadvantages of the algorithm

2.2 algorithm parameters

2.3 variants

3. Distance formula in the algorithm

4. Case realization

4.1 reading data

4.2 separate training set and test set

4.3 normalization

4.4 calculating Euclidean distance

4.5 # sorting and outputting test results

4.6 calculation accuracy

Total code

1. Basic definitions

k-nearest neighbor algorithm is a relatively simple machine learning algorithm. It uses the method of measuring the distance between different eigenvalues for classification. Its idea is very simple: if most of the samples of multiple nearest neighbors (most similar) in the feature space belong to a category, the sample also belongs to this category. The first letter k can be lowercase, indicating the number of externally defined nearest neighbors.

In short, let the machine itself according to the distance of each point, and the close ones are classified as one kind.

2. Algorithm principle

The core idea of knn algorithm is the category of unlabeled samples, which is decided by the nearest k neighbors.
Specifically, suppose we have a labeled data set. At this time, there is an unmarked data sample. Our task is to predict the category of this data sample. The principle of knn is to calculate the distance between the sample to be labeled and each sample in the data set, and take the nearest K samples. The category of the sample to be marked is generated by the voting of the k nearest samples.
Suppose X_test is the sample to be marked, X_train is a marked data set, and the pseudo code of algorithm principle is as follows:

1. Traverse x_ For all samples in the train, calculate the relationship between each sample and X_test and save the Distance in the Distance array.
2. Sort the Distance array, take the nearest k points and record them as X_knn.
3. In X_ Count the number of each category in KNN, that is, class0 is in X_ There are several samples in KNN, and class1 is in X_ There are several samples in KNN.
4. The category of samples to be marked is in X_ The KNN category with the largest number of samples.

2.1 advantages and disadvantages of the algorithm

• Advantages: high accuracy, high tolerance to outliers and noise.
• Disadvantages: large amount of calculation and large demand for memory.

2.2 algorithm parameters

The algorithm parameter is k, and the parameter selection needs to be determined according to the data.

• The larger the k value is, the greater the deviation of the model is, and the less sensitive it is to noise data. When the k value is large, it may cause under fitting;
• The smaller the k value, the greater the variance of the model. When the k value is too small, it will cause over fitting.

2.3 variants

There are some variants of knn algorithm, one of which can increase the weight of neighbors. By default, the same weight is used when calculating the distance. In fact, you can specify different distance weights for different neighbors. For example, the closer the distance, the higher the weight. This can be achieved by specifying the weights parameter of the algorithm.
Another variant is to replace the nearest k points with points within a certain radius. When the data sampling is uneven, it can have better performance. In scikit learn, the RadiusNeighborsClassifier class implements this algorithm variant.

3. Distance formula in the algorithm

Unlike our linear regression, we have no formula to deduce here. The core of KNN classification algorithm is to calculate the distance, and then classify according to the distance.

In the two-dimensional Cartesian coordinate system, I believe junior high school students should be familiar with this. He has a more common name, rectangular coordinate system. Among them, Euclidean distance is commonly used to calculate the distance between two points. Point A(2,3) and point B(5,6), then the distance of AB is

This is the Euclidean distance. However, there are some differences from what we often encounter. Euclidean distance can calculate multidimensional data, that is, matrix. This can help us solve many problems, so the formula becomes

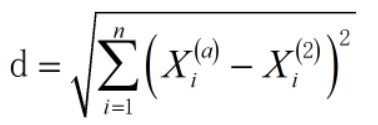
4. Case realization

We used the knn algorithm and its variants to predict the diabetes of Pina Indians. The dataset can be downloaded from below.
Link: LAN Zuoyun

4.1 reading data

%Read data
data=xlsread('D:\desktop\knn.xlsx');

4.2 separate training set and test set

ratio=0.1;%Proportion of test data
[N,M]=size(data);
trainData=data(:,1:8);
trainClass=data(:,9);
num_test=N*ratio;

4.3 normalization

%Normalization processing newData=(oldData-minValue)/(maxValue-minValue);
minValue=min(trainData);
maxValue=max(trainData);
trainData=(trainData-repmat(minValue,N,1))./(repmat(maxValue-minValue,N,1));

4.4 calculating Euclidean distance

%Calculate the Euclidean distance between the training data set and the test data dist
dist=zeros(N,1);
for i=1:N
    dist(i,:)=norm(trainData(i,:)-testData);
end

4.5 # sorting and outputting test results

%take dist Sort from small to large
[Y,I]=sort(dist,1);   
K=min(K,length(Y));
%The category corresponding to the training data corresponds to the sorting result of the training data
labels=trainClass(I);
%Before confirmation K Frequency of occurrence of the category of points
idx=mode(labels(1:K));%mode Mode of function
fprintf('The test data belongs to class %d  ',idx);

4.6 calculation accuracy

error=0;
for i=1:num_test
    idx=KNN(trainData(num_test+1:N,:),trainClass(num_test+1:N,:),trainData(i,:),K);
    fprintf('The real class of the test data is:%d\n',trainClass(i,:));
    if idx~=trainClass(i,:);
        error=error+1;
    end
end
fprintf('The accuracy is:%f\n',1-error/num_test);

Total code

clc;clear;
% Warning message elimination
warning('off');
%Read data
data=xlsread('D:\desktop\knn.xlsx');
ratio=0.1;%Proportion of test data
[N,M]=size(data);
K=4;
trainData=data(:,1:8);
trainClass=data(:,9);
num_test=N*ratio;
%Normalization processing newData=(oldData-minValue)/(maxValue-minValue);
minValue=min(trainData);
maxValue=max(trainData);
trainData=(trainData-repmat(minValue,N,1))./(repmat(maxValue-minValue,N,1));
error=0;
for i=1:num_test
    idx=KNN(trainData(num_test+1:N,:),trainClass(num_test+1:N,:),trainData(i,:),K);
    fprintf('The real class of the test data is:%d\n',trainClass(i,:));
    if idx~=trainClass(i,:);
        error=error+1;
    end
end
fprintf('The accuracy is:%f\n',1-error/num_test);

return:

Where KNN function:

function [ idx ] = KNN( trainData,trainClass,testData,K )
%UNTITLED Summary of this function goes here
%   Detailed explanation goes here


[N,M]=size(trainData);
%Calculate the Euclidean distance between the training data set and the test data dist
dist=zeros(N,1);
for i=1:N
    dist(i,:)=norm(trainData(i,:)-testData);
end
%take dist Sort from small to large
[Y,I]=sort(dist,1);   
K=min(K,length(Y));
%The category corresponding to the training data corresponds to the sorting result of the training data
labels=trainClass(I);
%{
%Before confirmation K Frequency of occurrence of the category of points
classNum=length(unique(trainClass));%Gets the number of single valued elements in the set
labels=zeros(1,classNum);
for i=1:K
    j=trainClass(i);
    labels(j)=labels(j)+1;
end
%Before return K The category with the highest frequency among the points is used as the prediction classification of the test data
[~,idx]=max(labels);
%}
%Before confirmation K Frequency of occurrence of the category of points
idx=mode(labels(1:K));%mode Mode of function
fprintf('The test data belongs to class %d  ',idx);
end