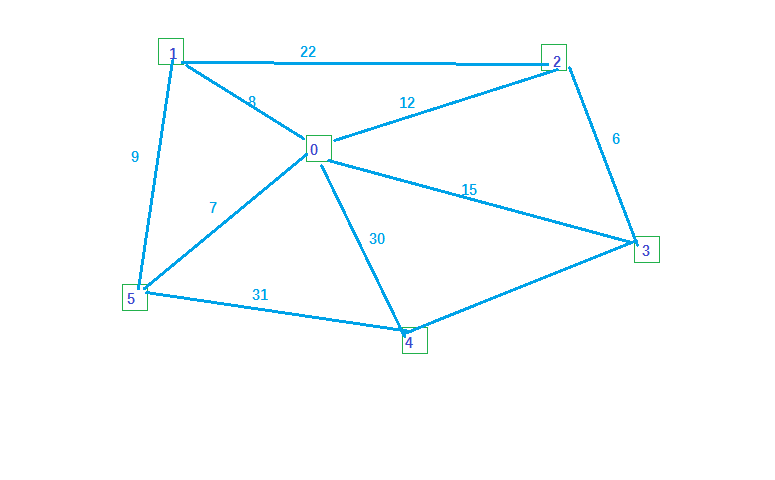
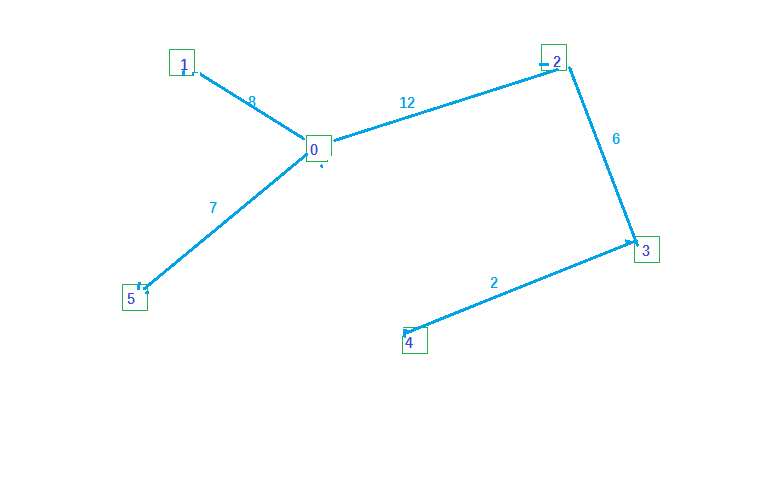
To generate the minimum tree is to select the right edge on an undirected connected graph, and to generate a sub connected graph satisfies the condition that the weight of all the edges is the least
Application: give the distance between n cities and each city, ask how to build and the length of the road if you want to build several roads to connect all cities...

The following is the minimum tree algorithm summarized and optimized by the black car driver

Data structure used
1. Node [set [i], the set to which node i belongs. At the beginning, it is I
2.size[i], the node contained in collection I, initially 1
3.edge[i], edge structure stores the information of undirected edges, including the weight of nodes and edges on both sides
General process:
1. Initialize data structure
2. Sort edge array in ascending order
3. Traverse the edge array. If the nodes on both sides of edge[i] come from different sets, combine them,
Until all nodes belong to the same collection.
Code and comments:

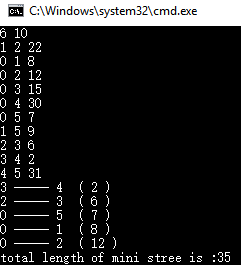
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<string>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
const int maxn = 100;

int node_set[maxn];	//the set node i belong to
int size[maxn];		//the munber of element that in set i
vector<int> ans;	//save the edge that take accepted

struct Edge{
	int node1;
	int node2;
	int val;
}edge[maxn];

void init(int n){
	for (int i = 0; i < n; i++){
		size[i] = 1;
		node_set[i] = i;
	}
	return;
}

int finds(int n){  //find the set node[n] belong to
	return(node_set[n] == n ? n : node_set[n] = finds(node_set[n]));
}
void show(){
	for (auto t : ans)
		printf("%d ----- %d  ( %d )\n", edge[t].node1, edge[t].node2, edge[t].val);
}
void connect(int a, int b){	//connect node a and node b, use it after make sure a and d come from different set 
	int as = finds(a);
	int bs = finds(b);
	if (size[as] <= size[bs]){
		node_set[as] = bs;
		size[bs]++;
	}
	else{
		node_set[bs] = as;
		size[as]++;
	}
	return;
}


int kruskal(int n){	//input the total munber of node return mini length conect all the node
	init(n);
	int len = 0;
	for (int i = 0; i < n; i++){
		if (finds(edge[i].node1) != finds(edge[i].node2)){
			connect(edge[i].node1, edge[i].node2);
			ans.push_back(i);
			len += edge[i].val;
		}
	}
	show(); 
	return len;
}
int main(){
	int n, m;  //munber of node and dege
	cin >> n >> m;
	for (int i = 0; i < m; i++) cin >> edge[i].node1 >> edge[i].node2 >> edge[i].val;
	sort(edge, edge + m, [](Edge &a, Edge &b){return a.val < b.val; });
	cout <<"total length of mini stree is :" << kruskal(n) << endl;		
}

/*
Data use case
6 10
1 2 22
0 1 8
0 2 12
0 3 15
0 4 30
0 5 7
1 5 9
2 3 6
3 4 2
4 5 31
*/

Operation results and analysis: