The most subtle thing in arranging a banquet is to arrange seats for all guests who come to the banquet. In any case, you can't line up two dead rivals at the same banquet table! This difficult task is now up to you. For any pair of guests, please write a program to tell the host whether they can be arranged at the same table.
Input format:

Input the first line and give three positive integers: n (≤ 100), that is, the total number of guests coming to the banquet, then these people are numbered from 1 to N; M is the number of known relationships between two guests; K is the number of queries. Then, in line m, each line gives the relationship between a pair of guests. The format is: guest 1 guest 2 relationship, where relationship 1 means friend and - 1 means sworn enemy. Note that two people cannot be both friends and enemies. Finally, K lines, each line gives a pair of guest numbers to be queried.

It is assumed that a friend's friend is also a friend. But the enemy of the enemy is not necessarily a friend, and the enemy of a friend is not necessarily an enemy. Only a simple and direct hostile relationship can never be at the same table.

Output format:

Output one line of results for each query: if two guests are friends and have no hostile relationship, output No problem; If they are not friends but are not hostile, output OK; If there is hostility between them, but they also have common friends, output OK but; If there is only hostile relationship between them, output No way.

Input sample:

7 8 4
5 6 1
2 7 -1
1 3 1
3 4 1
6 7 -1
1 2 1
1 4 1
2 3 -1
3 4
5 7
2 3
7 2

Output example:

No problem
OK
OK but...
No way

In fact, it is not difficult to understand the typical problem of parallel search. Here is my analysis:
When the input is 1, that is, two people are friends, use Union to put the two people together through parallel search. When the input is - 1 and two people are enemies, use the adjacency matrix to store the enemy information. Finally, it only needs to consider both. There are four situations: friends and no enemies; Friends, enemies; No friend, no enemy; Not a friend, but an enemy, corresponding to the code

if(findFather(a)==findFather(b)&&vis[a][b]==0){//The following four situations correspond to the above
			cout<<"No problem"<<endl;
		}
		else if(findFather(a)!=findFather(b)&&vis[a][b]==0){
			cout<<"OK"<<endl;
		}
		else if(findFather(a)==findFather(b)&&vis[a][b]==1){
			cout<<"OK but..."<<endl;
		}
		else{
			cout<<"No way"<<endl;
		}

Graphic analysis: drawing can help you understand better

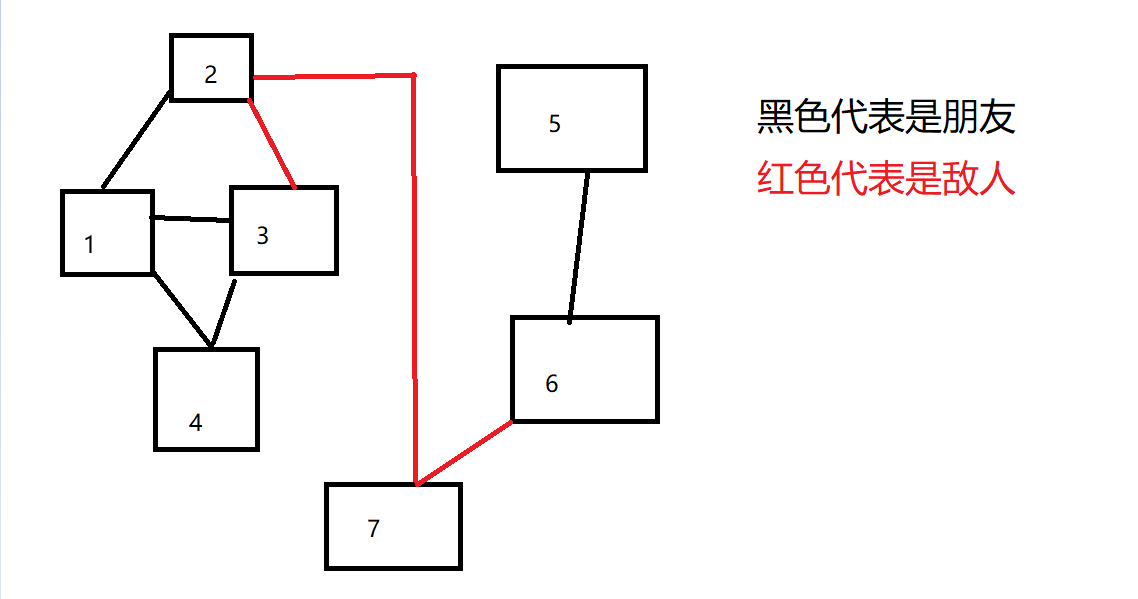
#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<set>
#include<stack>
#include<string>
#include<queue>
#include<vector>
#include<cctype>
#include<map>
using namespace std;
const int maxn=101;
int father[maxn];
int vis[maxn][maxn];
bool isRoot[maxn];
int n,m,k;
void init(){
	for(int i=1;i<=n;i++){
		father[i]=i;
		isRoot[i]=false;
	}
}
int findFather(int x){//Find root node
	if(x==father[x]){
		return x;
	}
	else{
		int F = findFather(father[x]);//Path compression
		father[x]=F;
		return F;
	}
}
void Union(int a,int b){
	int pa = findFather(a);
	int pb = findFather(b);
	if(pa!=pb){
		father[pa]=pb;
	}
}

int main(){
	cin>>n>>m>>k;
	init();
	while(m--){
		int a,b,t;
		cin>>a>>b>>t;
		if(t==1){
			Union(a,b);
		}
		else{
			vis[a][b]=vis[b][a]=1;//Enemy 
		}
	}
	while(k--){
		int a,b;
		cin>>a>>b;
		if(findFather(a)==findFather(b)&&vis[a][b]==0){
			cout<<"No problem"<<endl;
		}
		else if(findFather(a)!=findFather(b)&&vis[a][b]==0){
			cout<<"OK"<<endl;
		}
		else if(findFather(a)==findFather(b)&&vis[a][b]==1){
			cout<<"OK but..."<<endl;
		}
		else{
			cout<<"No way"<<endl;
		}
	}
}