This paper describes the generation of labyrinths and labyrinth routing algorithms.

 

 

////////////////////////////////////////////////////////////////////////////////////////////////////

1. Three Labyrinth Generation Algorithms

1. DFS (depth first) algorithm generation, which is divided into recursive and non-recursive methods.

(2) Cross-sectioning algorithm generation, which is divided into recursive and non-recursive methods.

3. Random Prim algorithm generation, a non-recursive method.

2. Two Labyrinth Path-finding Algorithms

1. DFS routing using non-recursive implementation.

2. A* Pathfinding, a non-recursive method.

 

 

////////////////////////////////////////////////////////////////////////////////////////////////////

Give some instructions before going into the explanation

1. Author's language: C++ (including some C++11 features).

2. Author's environment: Win10 + VS2019.

3. The interface after labyrinth generation is generated by the EasyX drawing library.

4. Visualizer of labyrinth algorithm made with EasyX, if necessary, please move to: https://codebus.cn/teternity/post/MazeAlgorithm

5. Unified requirements for labyrinths: all lengths and widths are odd (and the default lengths and widths are N), the outermost circle is the wall, the entry coordinates (0,1), and the exit coordinates (N-1, N-2).

6. This article was originally created by the author and does not involve copyright disputes. It is only for learning.

7. At a minimum, you need to be familiar with data structures such as stacks and queues, as well as some STL containers before reading the code, which will be mentioned later.

 

 

////////////////////////////////////////////////////////////////////////////////////////////////////

//Next to body

////////////////////////////////////////////////////////////////////////////////////////////////////

1. Three labyrinth generation algorithms (the periphery is a wall or an entrance, so the operation range is: (1, 1) to (N-2, N-2))

1. DFS algorithm generation (a wall-digging algorithm)

a. Initially all walls (N is odd):

　　　　　　　　

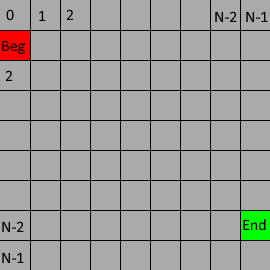
b, x,y are all odd numbers in 1~N-2 randomly select a point (that is, the coordinates of the point are all odd), dig it out, and stack the point

 　　　　　　　　

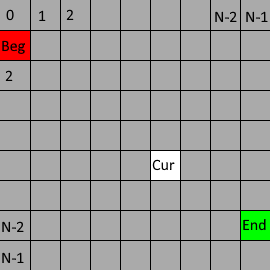
c. Choose one of the four directions randomly and set the current digging coordinates to (x, y).

If the direction satisfied (x + dx*2, y + dy*2) is a wall (dx and Dy represent direction, with a value of 1 or -1), dig open (x + dx, y + dy) and reset the current point to (x + dx*2, y + dy*2) to stack the current point

　　　　　　　　

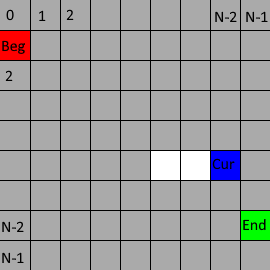
d. Repeat step c with Cur as current point

　　　　　　　　　　　　

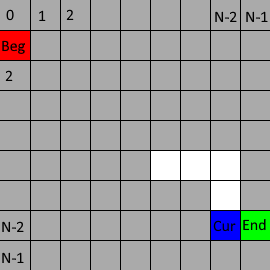
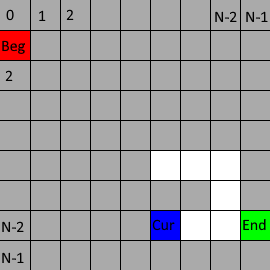
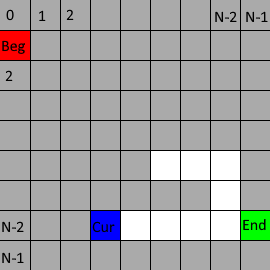
e. If Cur cannot dig the surrounding wall, the stack performs a pop operation and resets Cur to the top element in the stack at that time

f, until the stack is empty, indicating the end of the wall digging operation

At this point, the DFS wall-digging algorithm ends, looking back at the process as if it were a hamster hole with several constraints. In order to connect the starting point to the ending point, it is necessary to make the wall-digging point odd and not cause the current channel to dig through another channel.

Look at the maze shape generated by this algorithm (drawn by the EasyX library):

　　　　　　　　

Source code (contains both iterative and non-iterative version algorithms).Also: Note EasyX is drawn with EasyX, delete the code if it is not available:

#include <iostream>
#include <ctime>
#include <stack>
#include <vector>
#include <algorithm>
#include <easyx.h>
using namespace std;


// Labyrinth Lattice State
enum CellState: int { PATH = 0, WALL, FLAG };

// Labyrinth 2-D Point Structure
struct Point2
{
    int x, y;
    Point2(int _x, int _y) :x(_x), y(_y) {}
};

// Labyrinth size (odd number required)
const int mazeSize = 21;


// Labyrinth Generation Interface--Recursive Version
void DFS_generator(int _x, int _y, std::vector<std::vector<int>>& maze)
{
    // Define direction container
    std::vector<std::vector<int>> dir{ {1,0},{-1,0},{0,1},{0,-1} };
    // Random disruption of direction
    std::random_shuffle(dir.begin(), dir.end());
    // Recursive Labyrinth Generation
    maze[_x][_y] = PATH;
    for (int i = 0; i < 4; ++i)
    {
        if (_x + 2 * dir[i][0] >= 1 && _x + 2 * dir[i][0] <= mazeSize - 2 && _y + 2 * dir[i][1] >= 1 && _y + 2 * dir[i][1] <= mazeSize - 2
            && maze[_x + 2 * dir[i][0]][_y + 2 * dir[i][1]] == WALL)
        {
            maze[_x + dir[i][0]][_y + dir[i][1]] = PATH;
            DFS_generator(_x + 2 * dir[i][0], _y + 2 * dir[i][1], maze);
        }
    }
}

// Labyrinth Generation Interface--Iterative Edition
void DFS_iterative_generator(std::vector<std::vector<int>>& maze)
{
    // Define Stack Container
    std::stack<Point2> sp;
    // Define direction container
    std::vector<std::vector<int>> dir{ {1,0},{-1,0},{0,1},{0,-1} };
    // Require parameter to be odd
    Point2 temp((rand() % (mazeSize - 2) + 1) | 1, (rand() % (mazeSize - 2) + 1) | 1);
    sp.push(temp);
    // Subsequent iterations generate a maze and draw it
    while (!sp.empty())
    {
        if (maze[temp.x][temp.y] != PATH)
            maze[temp.x][temp.y] = PATH;
        // Random disruption of direction
        std::random_shuffle(dir.begin(), dir.end());
        int i = 0;
        for (; i < 4; ++i)
        {
            if (temp.x + 2 * dir[i][0] >= 1 && temp.x + 2 * dir[i][0] <= mazeSize - 2 && temp.y + 2 * dir[i][1] >= 1 && temp.y + 2 * dir[i][1] <= mazeSize - 2
                && maze[temp.x + 2 * dir[i][0]][temp.y + 2 * dir[i][1]] == WALL)
            {
                maze[temp.x + dir[i][0]][temp.y + dir[i][1]] = PATH;
                temp.x += 2 * dir[i][0];
                temp.y += 2 * dir[i][1];
                sp.push(temp);
                break;
            }
        }
        if (i == 4) sp.pop();
        if (!sp.empty()) temp = sp.top();
    }
}


// main function
int main()
{
    srand((unsigned)time(nullptr));

    // Entry and Exit
    Point2 start(0, 1);
    Point2 end(mazeSize - 1, mazeSize - 2);

    // Two-dimensional labyrinth container
    std::vector<std::vector<int>> maze;

    // Initialize maze
    for (int i = 0; i < mazeSize; ++i) maze.push_back(std::vector<int>());
    for (int i = 0; i < mazeSize; ++i)
        for (int j = 0; j < mazeSize; ++j)
            maze[i].push_back(WALL);
    maze[start.x][start.y] = maze[end.x][end.y] = PATH;

    // Maze Generation (Iterative and Non-Iterative alternative)
    DFS_generator((rand() % (mazeSize - 2) + 1) | 1, (rand() % (mazeSize - 2) + 1) | 1, maze);
    // DFS_iterative_generator(maze);

    // Print maze
    for (int j = 0; j < mazeSize; ++j)
    {
        for (int i = 0; i < mazeSize; ++i)
            cout << maze[i][j] << " ";
        cout << endl;
    }

    // EasyX
    {
        auto ret = _getwch();
        const int width = 15;
        initgraph(mazeSize * width, mazeSize * width);
        setlinecolor(DARKGRAY);
        setfillcolor(LIGHTGRAY);
        for (int j = 0; j < mazeSize; ++j)
            for (int i = 0; i < mazeSize; ++i)
                if (maze[i][j] == WALL)
                    fillrectangle(i * width, j * width, i * width + width - 1, j * width + width - 1);
        // saveimage(_T("D:\\maze.png"));
        ret = _getwch();
        closegraph();
    }

    return 0;
}

 

2. Generation of cross-sectioning algorithm (a cross-wall algorithm)

//

//