Preliminary of latex10 latex mathematical formula
close LaTeX tutorial 1
This lecture mainly discusses the problem of mathematical formulas in typesetting in LaTeX.
- For convenience, we can open the structure view of VSCode to view the structure of the document.
- The document content of LateX is divided into text mode and mathematical mode, which are used for typesetting ordinary documents and mathematical formulas respectively.
- The first is the in-line formula. The in-line formula can be typeset with a pair of single $symbols or with the parenthesis command, that is, the left and right parentheses led out by \. You can also use the math environment for typesetting, and the mathematical formula to be typeset is placed in these environments or commands. Such dollar symbols, parenthesis commands, and math environment are called mathematical patterns. Of course, content outside these commands or environments is called text mode. Compile and view the results to realize the correct layout of inter line formulas.
% Introduction area
\documentclass{article} % ctexbook, ctexrep
\usepackage{ctex}
\usepackage{amsmath}
% Text area(Document area)
\begin{document}
\section{brief introduction}
\LaTeX{}The typesetting content is divided into text mode and mathematical mode. Text mode is used for ordinary text typesetting, and mathematical mode is used for mathematical formula typesetting.
\section{Inline formula}
\subsection{Dollar sign}
The commutative law is $a+b=b+a$, as $1+2=2+1=3$.
\subsection{parentheses}
The commutative law is \(a+b=b+a\),as \(1+2=2+1=3\).
\subsection{math environment}
The commutative law is \begin{math}
a+b=b+a
\end{math}
,as \begin{math}
1+2=2+1=3
\end{math}.
\section{Superscript and subscript}
\subsection{Superscript}
\subsection{subscript}
\section{Greek alphabet}
\section{Mathematical function}
\section{fraction}
\section{Interline formula}
\subsection{Dollar sign}
\subsection{Bracket}
\subsection{displaymath environment}
\subsection{Automatic numbering formula equation environment}
\subsection{No numbering formula equation* environment}
\end{document}
- Of course, superscript and subscript are inevitably used in mathematical formulas.
- Superscript is typeset by ^ symbol.
\subsection{Superscript}
$3x^2 - x + 2 = 0$

- If we change the index to 20, compile and view the results
\subsection{Superscript}
$3x^20 - x + 2 = 0$

- Obviously, the required typesetting is not implemented. LaTeX only performs superscript processing on 2, but 0 does not. At this time, you need to use {} to form a group to realize the required typesetting. Compile and view the results. At this time, the typesetting results are correct.
\subsection{Superscript}
$3x^{20} - x + 2 = 0$

- In the mathematical model of LaTeX, an existing formula can even be treated as a superscript. Pay attention to using {}. Compile and view the results.
\subsection{Superscript}
$3x^{20} - x + 2 = 0$
$3x^{3x^{20} - x + 2} - x + 2 = 0$

- For the typesetting of subscripts, it is realized by underlining in LaTeX. Of course, if there are multiple characters in the subscript without grouping with {}, the subscript layout cannot be realized correctly.
\subsection{subscript}
$a_0, a_1, a_2$
$a_0, a_1, a_2, ..., a_100$

- At this time, all characters constituting subscripts need to be placed in {} to form a group. Pay attention to the results
\subsection{subscript}
$a_0, a_1, a_2$
$a_0, a_1, a_2, ..., a_{100}$

- Similarly, an existing formula can also be used as a subscript. At this time, pay attention to the use of {}. View results
\subsection{subscript}
$a_0, a_1, a_2$
$a_0, a_1, a_2, ..., a_{3x^{20} - x + 2}$

- Of course, Greek letters are also an important element of formulas. In LaTeX's mathematical model, you can directly use the corresponding commands to typeset Greek letters. These commands are English names corresponding to Greek letters. Pay attention to the results.
\section{Greek alphabet}
$\alpha$
$\beta$
$\gamma$
$\epsilon$
$\pi$
$\omega$
$\Gamma$
$\delta$
$\Theta$
$\Pi$
$\Omega$
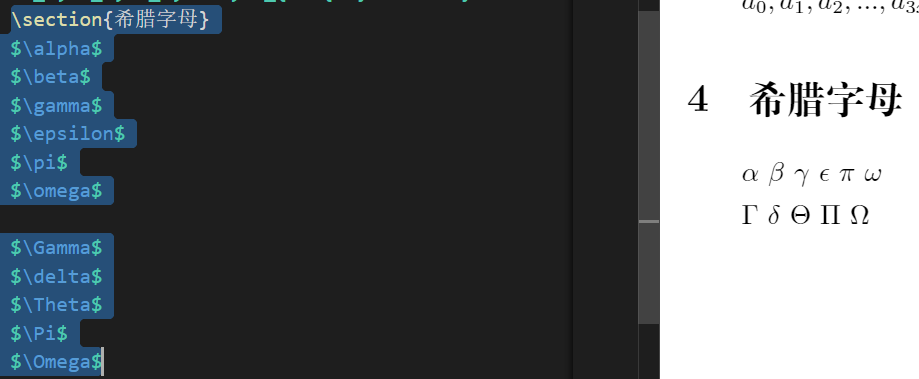
- Some commands that start with uppercase letters are used to typeset uppercase Greek letters. The Greek alphabet command can also be used in general formula typesetting. Pay attention to the results.
\section{Greek alphabet}
$\alpha$
$\beta$
$\gamma$
$\epsilon$
$\pi$
$\omega$
$\Gamma$
$\delta$
$\Theta$
$\Pi$
$\Omega$
$\alpha^3 + \beta^2 + \gamma = 0$
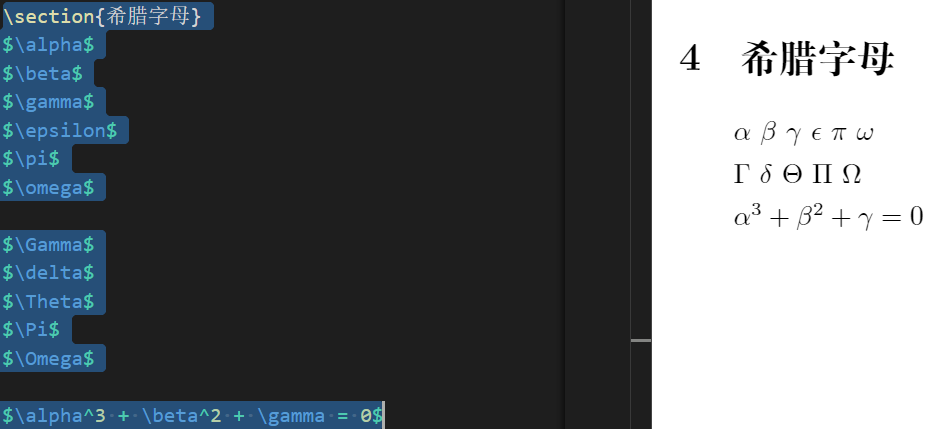
- For some commonly used functions, you can also use the corresponding commands for typesetting in the mathematical mode.
\section{Mathematical function}
$\log$
$\sin$
$\cos$
$\arcsin$
$\arccos$
$\ln$

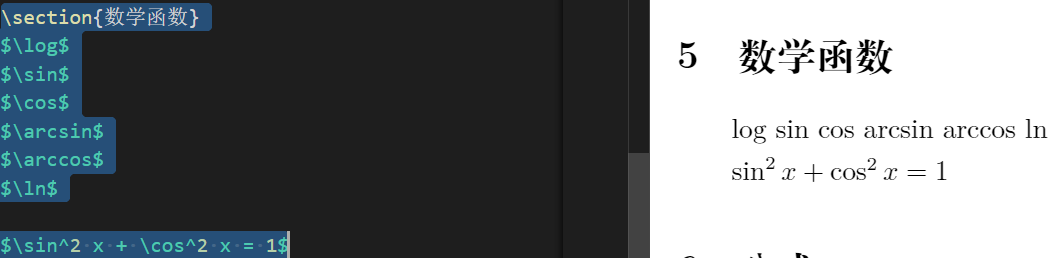
- And you can further form a formula. Pay attention to the results.
\section{Mathematical function}
$\log$
$\sin$
$\cos$
$\arcsin$
$\arccos$
$\ln$
$\sin^2 x + \cos^2 x = 1$
- You can also use superscripts and subscripts to form more complex formulas. Pay attention to the results.
\section{Mathematical function}
$\log$
$\sin$
$\cos$
$\arcsin$
$\arccos$
$\ln$
$\sin^2 x + \cos^2 x = 1$
$y = \arcsin x$
$y = \sin^{-1} x$
$y = \log_2 x$
$y = \ln x$

- Another special command is the \ sqrt command, which is used for typesetting roots. By combining with superscript and subscript and nesting with each other, complex formulas can be generated. You can also specify the number of squares through the optional parameter of the \ sqrt command. Pay attention to the results.
\section{Mathematical function}
$\log$
$\sin$
$\cos$
$\arcsin$
$\arccos$
$\ln$
$\sin^2 x + \cos^2 x = 1$
$y = \arcsin x$
$y = \sin^{-1} x$
$y = \log_2 x$
$y = \ln x$
$\sqrt{2}$
$\sqrt{x^2 + y^2}$
$\sqrt{2 + \sqrt{2}}$
$\sqrt[4]{x}$
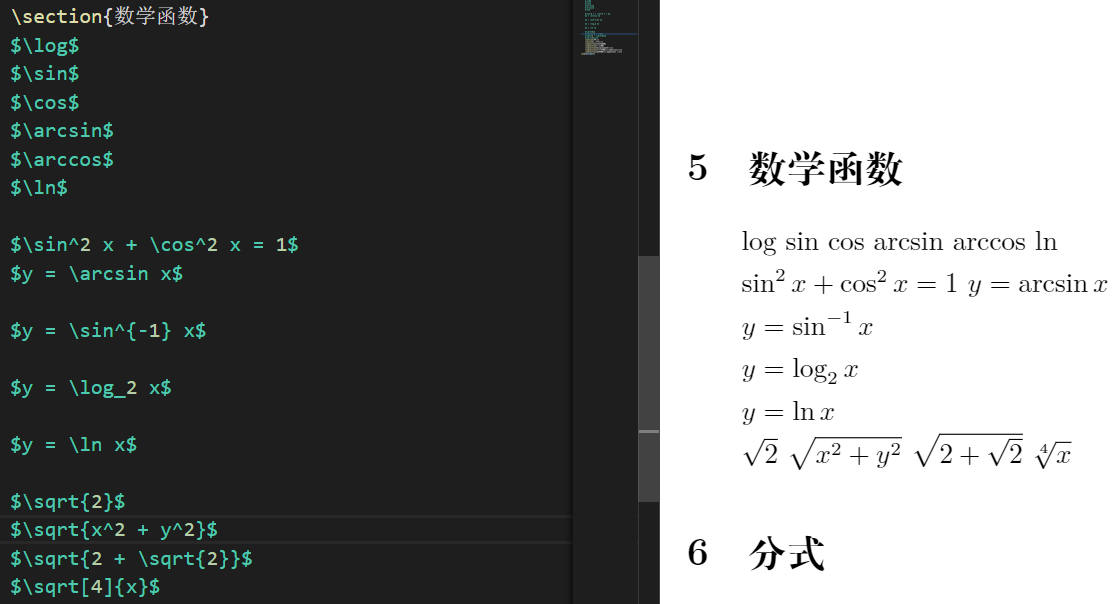
- Of course, fraction is also a common constituent element in formula composition. You can enter fractions directly in mathematical mode or use the \ frac command to typeset fractions. The first required parameter of the command is numerator and the second required parameter is denominator. Compile and view the results.
\section{fraction}
About the original volume $3/4$.
About the original volume $\frac{3}{4}$.

- Of course, you can also combine the \ frac command with superscript and subscript and other formula layout commands to form more complex formulas. Compile and view the results.
\section{fraction}
About the original volume $3/4$.
About the original volume $\frac{3}{4}$.
$\frac{x}{x^2 + x + 1}$
$\frac{\sqrt{x - 1}}{\sqrt{x + 1}}$
$\frac{1}{1 + \frac{1}{x}}$
$\sqrt{\frac{x}{x^2 + x + 1}}$

- Another type of formula is the interline formula. A pair of double knife music symbol typesetting inter line formulas can be used to put the formulas in the mathematical model of double to music. Compile and view the results.
\section{Interline formula}
The commutative law is $$a+b=b=a$$,as $$1+2=2+1=3$$

- The format of the source code can be adjusted appropriately to make the code clearer. Note that there is an extra comma here, which can be deleted directly.
\subsection{Dollar sign}
The commutative law is $$a+b=b=a$$
as
$$1+2=2+1=3$$

- You can also use the bracketed commands for formula layout between lines, that is, the left and right square brackets commands derived from \.
\subsection{Bracket}
The commutative law is
\[a+b=b+a\]
as
\[1+2=2+1=3\]

- You can also use the displaymath environment to format inter line formulas. As you can see, the results are the same.
\subsection{displaymath environment}
The commutative law is
\begin{displaymath}
a+b=b+a,
\end{displaymath},
as
\begin{displaymath}
1+2=2+1=3.
\end{displaymath}

- If the formula needs to be numbered automatically, the equation environment needs to be used for formula typesetting. Put the formula to be typeset in the equation environment and pay attention to the results.
\subsection{Automatic numbering formula equation environment}
\begin{equation}
a+b=b+a
\end{equation}

- LaTeX numbers the formula automatically. You can also use the \ label command to label formulas in the equation environment. At any position, we can reference this label through the \ ref command to realize cross reference of formulas. Compile and view the results to achieve the correct cross reference.
\subsection{Automatic numbering formula equation environment}
See formula for commutative law\ref{eq:commutative}
\begin{equation}
a+b=b+a \label{eq:commutative}
\end{equation}
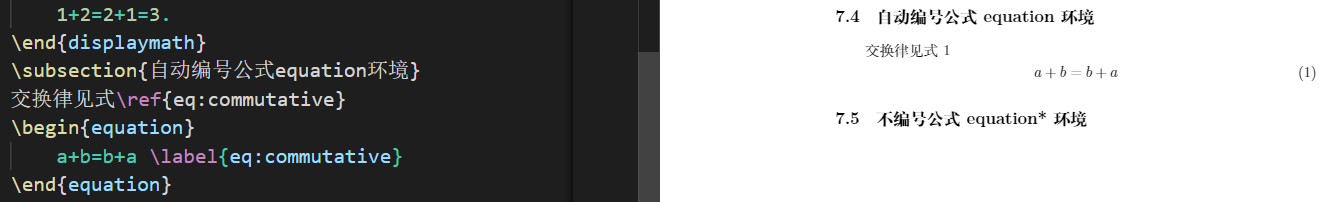
- If the formula does not need to be numbered, we can use the equation environment with * for typesetting. You can also use the \ label and \ ref commands to implement cross referencing.
\subsection{No numbering formula equation*environment}
See formula for commutative law\ref{eq:commutative2}
\begin{equation*}
a+b=b+a \label{eq:commutative2}
\end{equation*}

- Note that the cross reference number is the summary number at this time.
- It should be noted that the number and cross reference of publicity are also realized automatically. In typesetting, we should get used to dealing with the number and cross reference of figures, tables and formulas in an automatic way.
- Here, add another inter line formula and use the \ label and \ ref commands to realize cross reference.
\begin{equation}
x^5 - 7x^3 + 4x = 0 \label{eq:pol}
\end{equation}

- Delete the previous inter line formula by annotation. Pay attention to the result. Cancel the annotation of the inter line formula again. Check the result again. It can be seen that LaTeX can automatically process various numbers and cross references.
- In addition, it should be noted that the equation environment with * needs to use the amspath macro package.
Code of this section:
% Introduction area
\documentclass{article} % ctexbook, ctexrep
\usepackage{ctex}
\usepackage{amsmath}
% Text area(Document area)
\begin{document}
\section{brief introduction}
\LaTeX{}The typesetting content is divided into text mode and mathematical mode. Text mode is used for ordinary text typesetting, and mathematical mode is used for mathematical formula typesetting.
\section{Inline formula}
\subsection{Dollar sign}
The commutative law is $a+b=b+a$, as $1+2=2+1=3$.
\subsection{parentheses}
The commutative law is \(a+b=b+a\),as \(1+2=2+1=3\).
\subsection{math environment}
The commutative law is \begin{math}
a+b=b+a
\end{math}
,as \begin{math}
1+2=2+1=3
\end{math}.
\section{Superscript and subscript}
\subsection{Superscript}
$3x^{20} - x + 2 = 0$
$3x^{3x^{20} - x + 2} - x + 2 = 0$
\subsection{subscript}
$a_0, a_1, a_2$
$a_0, a_1, a_2, ..., a_{3x^{20} - x + 2}$
\section{Greek alphabet}
$\alpha$
$\beta$
$\gamma$
$\epsilon$
$\pi$
$\omega$
$\Gamma$
$\delta$
$\Theta$
$\Pi$
$\Omega$
$\alpha^3 + \beta^2 + \gamma = 0$
\section{Mathematical function}
$\log$
$\sin$
$\cos$
$\arcsin$
$\arccos$
$\ln$
$\sin^2 x + \cos^2 x = 1$
$y = \arcsin x$
$y = \sin^{-1} x$
$y = \log_2 x$
$y = \ln x$
$\sqrt{2}$
$\sqrt{x^2 + y^2}$
$\sqrt{2 + \sqrt{2}}$
$\sqrt[4]{x}$
\section{fraction}
About the original volume $3/4$.
About the original volume $\frac{3}{4}$.
$\frac{x}{x^2 + x + 1}$
$\frac{\sqrt{x - 1}}{\sqrt{x + 1}}$
$\frac{1}{1 + \frac{1}{x}}$
$\sqrt{\frac{x}{x^2 + x + 1}}$
\section{Interline formula}
\subsection{Dollar sign}
The commutative law is $$a+b=b=a$$
as
$$1+2=2+1=3$$
\subsection{Bracket}
The commutative law is
\[a+b=b+a\]
as
\[1+2=2+1=3\]
\subsection{displaymath environment}
The commutative law is
\begin{displaymath}
a+b=b+a,
\end{displaymath}
as
\begin{displaymath}
1+2=2+1=3.
\end{displaymath}
\subsection{Automatic numbering formula equation environment}
See formula for commutative law\ref{eq:commutative}
\begin{equation}
a+b=b+a \label{eq:commutative}
\end{equation}
\subsection{No numbering formula equation*environment}
See formula for commutative law\ref{eq:commutative2}
\begin{equation*}
a+b=b+a \label{eq:commutative2}
\end{equation*}
It should be noted that the number and cross reference of publicity are also realized automatically,
In typesetting, we should get used to using automatic methods to deal with problems such as drawings
Numbering and cross referencing of tables and formulas. Another example is the formula\ref{eq:pol}:
\begin{equation}
x^5 - 7x^3 + 4x = 0 \label{eq:pol}
\end{equation}
\end{document}