J - Cunning Friends

Game theory:

Main idea of the title: give n buckets, each bucket has several small balls, three people play the game, the first hand operates first, and the remaining two people are a group. If you want the first hand to lose, three people play the game in turn. Each candidate takes out > 0 balls in a bucket. When one person cannot operate, he loses
The two men behind wanted the first player to lose and asked if the first player could win the game

Find the rule by typing the table:

typedef int itn;
int n, m;
int eq, da, xiao;
int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) {
		int x = read;
		if (x > 2) da++;
		else if (x == 2) eq++;
		else xiao++;
	}
	if (da == 1) da--, eq++;
	if (da > 1) puts("Lose");
	else if (eq > 2) puts("Lose");
	else if (eq == 1) puts("Win");
	else {
		if (xiao % 3) puts("Win");
		else puts("Lose");
	}
	return 0;
}

/*
2 10
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
AB
ABBBBABBBB

10
*/

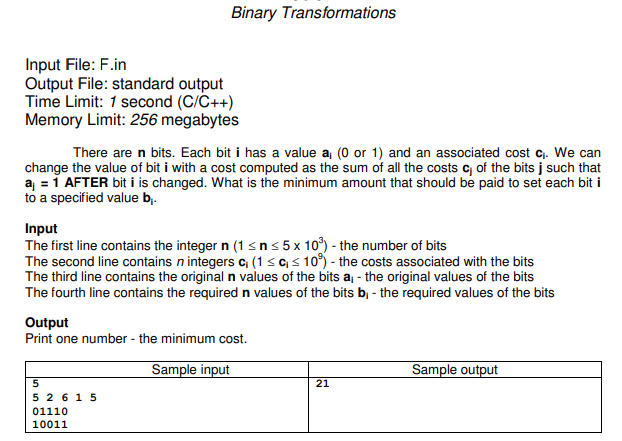
F - Binary Transformations

Thinking greed
First, a wrong greedy strategy:
First convert all parts that should be 1 - > 0, and then convert all parts that should be 0 - > 1
In the process of 1 - > 0, it is processed according to the weight from large to small;
In the process of 0 - > 1, it is processed from small to large according to the weight;
This may be optimal in some cases

However, when there is a position where both bits are 1 and the weight is very, very large, we can first convert the number to 0, and then carry out the above operations. Another thing is, if there are several positions in this case, which part should be converted? In other words, we should convert fewer to meet the optimal greedy?
Because when the above two positions correspond to 1, the conversion to 0 also has a price!

Here is the source of ideas, which can solve this situation well Blog link
Practice: if there is no position p (a[p]=1,b[p]=1), the answer is to greedily change all 1 from large to small to 0, and all 0 from small to large to 1. If there are some positions P, we will enumerate how many p we turn into 0 at the beginning. Obviously, the greater the value of P, the better. Now consider how to simulate. We can use two set s. One maintains the number that needs to change from 0 to 1 at the beginning, and the other maintains the number that needs to change from 1 to 0 at the end. Insert O(log n), traverse O(n), and the total complexity O(n2)

Here is my personal understanding:
Because the transformation will contribute to the answer if both are 1, we should consider inserting the case where both are 1
As mentioned earlier, the process of 1 - > 0 should be carried out in the order from large to small, but in the process of using set maintenance, the default order is from small to large, so an inverse iterator should be used; In the process of 0 - > 1, the operation is carried out in the order from small to large, and it is ok to traverse it with an iterator
Because when considering the case that both values are 1, the higher the cost, it may make a greater contribution to the answer. In the process of insertion, the order from large to small should be considered
Record the minimum contribution of the operation

typedef int itn;
int n;
ll a[maxn];
string s,t; 
ll sum = 0,ans = 0;
vector<ll> vet;
multiset<ll> st1,st2;
bool cmp(ll a,ll b){
	return a > b;
}
ll get(int x){
	ll ret = 0;
	ll s = sum;
	int pos = x;
	if(pos) st1.insert(vet[pos-1]),st2.insert(vet[pos-1]);
	multiset<ll> :: iterator it1;
	multiset<ll> :: reverse_iterator it2;
	/// 1-> 0  big -> small
	for(it2 = st1.rbegin();it2 != st1.rend();++it2){
		s -= *(it2);
		ret += s;
	}
	for(it1 = st2.begin();it1 != st2.end(); ++ it1){
		s += *(it1);
		ret += s;
	}
	return ret;
}
int main() {
	cin >> n;
	for(int i=1;i<=n;i++) cin >> a[i];
	cin >> s;
	cin >> t;
	s = "#" + s;
	t = "#" + t;
	for(int i=1;i<=n;i++){
		if(s[i] == '1') sum += a[i];
		if(s[i] != t[i]) {
			if(s[i] == '1') st1.insert(a[i]);
			else st2.insert(a[i]);
		}else if(s[i] == '1'){
			vet.push_back(a[i]);
		}
	}
	sort(vet.begin(),vet.end(),cmp);
	int siz = vet.size();
	ll ans = inf;
	// cout <<"ans :  " << ans <<endl;
	for(itn i=0;i<=siz;i++){
		ans = min(ans,get(i));
	}
	cout << ans <<endl;
	return 0;
}