Learning notes - dynamic programming

Dakeng series

Dynamic programming = pusher + initialization + various optimizations

Ordinary dp

1. Backpack dp

There are several kinds of backpacks:

<1> 0-1 Backpack

P1048 medicine collection

First, we set the weight \ (w(i) \) and value \ (v(i) \) of the \ (I \) th "item" and the capacity of the backpack as \ (W \). It is easy to find that this state transition is the problem of "take or not take, buy or not buy". Setting \ (dp_{i,j} \) represents the maximum value that can be obtained when the price of the first \ (I \) item is \ (j \). Since it is converted from buy or not buy, we can get:

\[dp_{i,j}=\max(dp_{i-1,j},dp_{i-1,j-w(i)}+v(i)) \]

The code implementation is:

int main(){
	m=read(),n=read();
	for(int i=1;i<=n;i++){
		w[i]=read(),v[i]=read();
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(w[i]>j){
				dp[i][j]=dp[i-1][j];
			}
			else{
				dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
			}
		}
	}
	printf("%d\n",dp[n][m]);
	return 0;
}

It should be noted that if the current price is not enough to take the \ (I \) item, that is, when there is no choice, you also need to update \ (dp_{i,j} \), you can find that the spatial complexity is not good enough, and you can roll out the first dimension. It becomes:

\[dp_j=\max(dp_j,dp_{j-w(i)}+v(i)) \]

Note that the reverse order should be used in the second dimension here. Considering that this array actually assigns the corresponding value to the result of the \ (i-1 \) in the \ (I \) th cycle, that is, it only needs to judge the \ ([w(i),W] \) part. In order to prevent the result of \ (dp_{j-w(i)} \) from being wrong by updating \ (dp_j \) first, choose to traverse from large to small, that is, reverse order.

int main(){
	m=read(),n=read();
	for(int i=1;i<=n;i++){
		w[i]=read(),v[i]=read();
	}
	for(int i=1;i<=n;i++){
		for(int j=m;j>=w[i];j--){
			dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
		}
	}
	printf("%d\n",dp[m]);
	return 0;
}

<2> Complete Backpack

P1616 crazy medicine collection

You can add an infinite number of items to each layer of backpack, that is, 0-0:

\[dp_{i,j}=\max_{k=0}^{+\infty}\{dp_{i-1,j-w(i)\times k}+v(i)\} \]

Time complexity \ (O(nmk) \), the coverage problem mentioned in 0-1 knapsack above can also be understood as the situation of selecting one item many times, which just meets the requirements of complete knapsack, so there are:

\[dp_j=\max(dp_j,dp_{j-w(i)}+v(i)) \]

Just change the reverse order to positive order.

int main(){
	m=read(),n=read();
	for(int i=1;i<=n;i++){
		w[i]=read(),v[i]=read();
	}
	for(int i=1;i<=n;i++){
		for(int j=w[i];j<=m;j++){
			dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
		}
	}
	printf("%d\n",dp[m]);
	return 0;
}

<3> Multiple Backpack

P1776 treasure screening

For each item \ (i \), add a quantity limit \ (k(i) \).

According to the enumeration formula of complete knapsack, we can get:

\[dp_{i,j}=\max_{k=0}^{k(i)}\{dp_{i-1,j-w(i)\times k}+v(i)\} \]

Of course, the complexity of this formula contains a \ (\ sum k(i) \), how to optimize it?

Binary optimization

In principle, it can be understood that if a number \ (p \) is divided into \ (q \) in binary, that is, \ (1,2,4,8,16 \), any number in \ ([0,p] \) can be obtained by adding these \ (q \) numbers. In that case, it is better to treat this item as a binary split \ (q \) item and treat it as a 0-1 knapsack.

int main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++){
		int tmpv=read(),tmpw=read(),k=read();
		for(int j=1;j<=k;j<<=1){
			v[++cnt]=j*tmpv,w[cnt]=j*tmpw;
			k-=j;
		}
		if(k) v[++cnt]=k*tmpv,w[cnt]=k*tmpw;
	}
	for(int i=1;i<=cnt;i++){
		for(int j=m;j>=w[i];j--){
			dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
		}
	}
	printf("%d\n",dp[m]);
	return 0;
}

<4> Hybrid Backpack

P1833 Cherry Blossom

Mix the above three DPS together

int main(){
	scanf("%d:%d%d:%d%d",&sh,&sm,&eh,&em,&n);
	m=eh*60+em-sh*60-sm;
	//printf("%d %d %d %d\n",sh,sm,eh,em);
	for(int i=1;i<=n;i++){
		int a=read(),b=read(),c=read();
		if(!c) c=1e6;
		for(int j=1;j<=c;j<<=1){
			w[++cnt]=a*j,v[cnt]=b*j;
			c-=j;
		}
		if(c) w[++cnt]=a*c,v[cnt]=b*c;
	}
	for(int i=1;i<=cnt;i++){
		for(int j=m;j>=w[i];j--){
			dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
		}
	}
	printf("%d\n",dp[m]);
	return 0;
}

<5> Two dimensional cost Backpack

P1855 extract kkksc03

Knapsack dp with double cost limitation is naturally handled by adding a layer of circulation.

int main(){
	n=read(),w1[0]=read(),w2[0]=read();
	for(int i=1;i<=n;i++){
		w1[i]=read(),w2[i]=read();
	}
	for(int i=1;i<=n;i++){
		for(int j=w1[0];j>=w1[i];j--){
			for(int k=w2[0];k>=w2[i];k--){
				dp[j][k]=max(dp[j][k],dp[j-w1[i]][k-w2[i]]+1);
			}
		}
	}
	printf("%d\n",dp[w1[0]][w2[0]]);
	return 0;
}

<6> Group Backpack

P1757 group backpack of Tongtian

If there are conflicting restrictions, use \ (vector \) to save the group, and then normal 0-1 backpack.

int main(){
	m=read(),n=read();
	for(int i=1;i<=n;i++){
		w[i]=read(),v[i]=read();
		int k=read();
		cnt=max(cnt,k);
		g[k].push_back(i);
	}
	for(int i=1;i<=cnt;i++){
		for(int j=m;j>=0;j--){
			for(int k=0;k<g[i].size();k++){
				int now=g[i][k];
				if(j>=w[now]){
					dp[j]=max(dp[j],dp[j-w[now]]+v[now]);
				}
			}
		}
	}
	printf("%d\n",dp[m]);
	return 0;
}

Examples

1.New year's fun cards

First, our target answer should be the difference between the total weight \ (sum \) and the current weight \ (W \). Use \ (dp(i) \) to represent the number of schemes. The recursive formula is the same as that of 0-1 knapsack. While the state is changing, use \ (addmark(i) \) to represent the number of cards added to the original card. Finally, judge the number of schemes and recursively output the required cards.

inline void print(int k){
	if(k){
		print(k-w[addmark[k]]);
		printf("%d",addmark[k]);
		if(k!=m) printf(" ");
	}
	return;
}
int main(){
	m=read(),n=read();
	for(int i=1;i<=n;i++){
		w[i]=read();
		sum+=w[i];
	}
	m=sum-m;
	dp[0]=1;
	for(int i=1;i<=n;i++){
		for(int j=m;j>=w[i];j--){
			dp[j]+=dp[j-w[i]];
			if(dp[j]>5){
				dp[j]=2;
			}
			if(!addmark[j]&&dp[j-w[i]]){
				addmark[j]=i;
			}
		}
	}
	if(!dp[m]) printf("0\n");
	else if(dp[m]>1) printf("-1\n");
	else print(m);
	return 0;
}

2. Linear dp

It can only be said that it is very non fancy dp.

Examples

1. Find the longest ascending subsequence

Let \ (dp_i \) represent the maximum ascending sequence length ending with \ (a_i \). It is obvious that the transfer equation is:

\[dp_i=\max_{j=1}^{i-1}(dp_j+1) [a_i>a_j] \]

The output subsequence is the same as storing the penultimate subscript and then backtracking.

inline void print(int pos){
	if(pos==-1) return;
	print(path[pos]);
	printf("%d ",a[pos]);
}
string s;
int main(){
	getline(cin,s);
	for(int i=0;i<s.size();i++){
		if(s[i]==' '){
			n++;
			continue;
		}
		a[n]=a[n]*10+s[i]-'0';
	}
	for(int i=1;i<=n;i++){
		path[i]=-1;
	}
	for(int i=1;i<=n;i++){
		dp[i]=1;
		for(int j=1;j<i;j++){
			if(a[i]>a[j]&&dp[j]+1>dp[i]){
				dp[i]=dp[j]+1;
				path[i]=j;
			}
		}
		if(dp[i]>ans){
			ans=max(ans,dp[i]);
			last=i;
		}
	}
	printf("max=%d\n",ans);
	print(last);
	return 0;
}

2.P1091 NOIP2004 improve group singing formation

Form of observation condition sequence:

\[t_i<t_2<\dots <t_i>\dots>t_{k-1}>t_k(1\leq i\leq k) \]

In essence, it is composed of the longest rising sequence on the left side of \ (t_i \) and the longest falling sequence on the right side. Then calculate the rising and falling sequence length with \ (t_i \) as the head and tail respectively, and finally sum and compare the size. The answer is:

\[ans=n-\max_{i=1}^n(dp1(i)+dp2(i)-1) \]

int main(){
	n=read();
	for(int i=1;i<=n;i++){
		a[i]=read();
	}
	for(int i=1;i<=n;i++){
		dp1[i]=1;
		for(int j=1;j<i;j++){
			if(a[i]>a[j]){
				dp1[i]=max(dp1[i],dp1[j]+1);
			}
		}
	}
	for(int i=n;i>=1;i--){
		dp2[i]=1;
		for(int j=n;j>i;j--){
			if(a[i]>a[j]){
				dp2[i]=max(dp2[i],dp2[j]+1);
			}
		}
	}
	for(int i=1;i<=n;i++){
		ans=max(ans,dp1[i]+dp2[i]-1);
	}
	printf("%d\n",n-ans);
	return 0;
}

3.P1020 NOIP1999 universal group missile interception

First, ask the longest Non rising subsequence, which is very easy to do.

The second question needs to be used Dilworth theorem The general meaning is that the number of Non rising subsequences required is equal to the length of the longest rising subsequence, which can be done in the same way.

4.P2196 NOIP1996 mine excavation by improvement group

The adjacency matrix records the path (actually a directed graph). Set \ (dp_i \) to represent the maximum value ending with \ (I \), and output the path in a backtracking manner.

5.P2782 Sister Cities

Sort each pair of sister cities in ascending order on the north bank, and then find the longest subsequence on the south bank, which requires a better \ (O(nlogn) \) algorithm

6.P1481 demon family password

The essence of finding the longest prefix chain is the same as that of the longest ascending subsequence. As to whether it is a prefix, you can use \ (hash \) or simply and roughly use \ (s.substr(pos,len) \) to represent the part of the string \ (s[pos:pos+len-1] \).

int main(){
	n=read();
	for(int i=1;i<=n;i++){
		cin>>s[i];
	}
	for(int i=1;i<=n;i++){
		dp[i]=1;
		for(int j=1;j<i;j++){
			int len=s[j].size();
			if(s[j]==s[i].substr(0,len)){
				dp[i]=max(dp[i],dp[j]+1);
			}
		}
		ans=max(ans,dp[i]);
	}
	printf("%d\n",ans);
	return 0;
}

7. Find the longest common subsequence

For arrays \ (s1(i) \) and \ (s2(j) \), set \ (dp(i,j) \) to represent the longest common subsequence length of cut-off \ (s1(i) \) and \ (s2(j) \). It is easy to find that \ (dp(i,j) \) can only be transferred from \ (dp(i-1,j-1) \), \ (dp(i-1,j) \) or \ (dp(i,j-1) \), so:

\[dp(i,j)=\max(dp(i-1,j),dp(i,j-1)) \]

\[dp(i,j)=\max(dp(i,j),dp(i-1,j-1))[s1(i)=s2(j)] \]

If the longest continuous common subsequence is found, \ (dp(i,j) \) represents the longest continuous common subsequence ending with \ (s1(i) \) and \ (s2(j) \), which will be transferred only when \ (s1(i)=s2(j) \).

//Discontinuous
int main(){
	scanf("%s",s1+1);
	scanf("%s",s2+1);
	len1=strlen(s1+1),len2=strlen(s2+1);
	for(int i=1;i<=len1;i++){
		for(int j=1;j<=len2;j++){
			dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
			if(s1[i]==s2[j]){
				dp[i][j]=dp[i-1][j-1]+1;
			}
		}
	}
	printf("%d\n",dp[len1][len2]);
	return 0;
}

//continuity
int main(){
	scanf("%s",s1+1);
	scanf("%s",s2+1);
	len1=strlen(s1+1),len2=strlen(s2+1);
	for(int i=1;i<=len1;i++){
		for(int j=1;j<=len2;j++){
			if(s1[i]==s2[j]){
				dp[i][j]=dp[i-1][j-1]+1;
			}
			ans=max(ans,dp[i][j]);
		}
	}
	printf("%d\n",ans);
	return 0;
}

8.P2904 River Crossing S

Obviously, prefix and optimization are needed, \ (sum(i)=sum(i-1)+a(i) \), and we add the transportation cost originally needed to him (note that the return trip is empty, so it only needs the cost of \ (m \), that is \ (sum(i)=sum(i)+m\times 2 \), and then use \ (dp(i) \) to represent the minimum cost of \ (I \) cattle before transportation, which can be transferred by double-layer circulation.

int main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++){
		dp[i]=maxxn;
		a[i]=read();
		sum[i]=sum[i-1]+a[i];
	}
	for(int i=1;i<=n;i++){
		sum[i]+=2*m;
	}
	for(int i=1;i<=n;i++){
		for(int j=i;j<=n;j++){
			dp[j]=min(dp[j],dp[j-i]+sum[i]);
		}
	}
	printf("%d\n",dp[n]-m);
	return 0;
}

9.P2285 HNOI2004 beating mole

It looks like three-dimensional, but it's actually one-dimensional.

It can be found that if you want to hit the \ (i \) and \ (j \) moles, the Manhattan distance between them (the sum of the distances parallel to the \ (x \) axis and the \ (y \) axis) needs to be less than or equal to the time difference, which is represented by \ (dis(i,j) \) and \ (t(i,j) \), According to the judgment method, use \ (dp(i) \) to indicate how many moles can be hit at most when hitting the \ (i \) mole. Readily available:

\[dp(i)=\max_{j=1}^{i-1}x\{dp(j)+1\}[dis(i,j)<=t(i,j)] \]

int main(){
	n=read(),m=read();
	for(int i=1;i<=m;i++){
		a[i].t=read(),a[i].x=read(),a[i].y=read();
	}
	for(int i=1;i<=m;i++){
		dp[i]=1;
		for(int j=1;j<i;j++){
			if(abs(a[i].t-a[j].t)>=abs(a[i].x-a[j].x)+abs(a[i].y-a[j].y)){
				dp[i]=max(dp[i],dp[j]+1);
			}
		}
		ans=max(ans,dp[i]);
	}
	printf("%d\n",ans);
	return 0;
}

So it's just a graph with special distance.

3. Coordinate dp

It's more like interval dp, basically considering the transfer direction or building a map.

Examples

1. Matrix retrieval (simple version)

Take the element from the head or tail of the queue in the sequence, take the (k) element for the \ (i \) th time, and the contribution to the answer is \ (a(k)\times 2^i \), and find the maximum value of the answer.

We use \ (dp(i,j) \) to indicate the maximum answer we have taken when taking the remaining interval \ ([i,j] \). It is not difficult to find \ (dp(i,i)=a(i)\times 2^n \), so the interval \ ([i,j] \) must be derived from \ ([i+1,j] \) or \ ([i,j-1] \) taking \ (I \) or \ (j \). If \ (l=j-i \), there is a transfer equation:

\[dp(i,j)=\max(dp(i+1,j)+a(i)\times 2^{n-l},dp(i,j-1)+a(j)\times 2^{n-l}) \]

inline ll q_pow(ll x,ll p){
	ll ans=1;
	while(p){
		if(p&1){
			ans=ans*x;
		}
		p>>=1;
		x=x*x;
	}
	return ans;
}
int main(){
	n=read();
	for(int i=1;i<=n;i++){
		a[i]=read();
		dp[i][i]=a[i]*q_pow(2,n);
	}
	for(int l=1;l<n;l++){
		for(int i=1,j=i+l;j<=n;i++,j=i+l){
			dp[i][j]=max(dp[i+1][j]+a[i]*q_pow(2,n-l),dp[i][j-1]+a[j]*q_pow(2,n-l));
		}
	}
	printf("%lld\n",dp[1][n]);
	return 0;
}

However, the advanced version needs to be written with high precision

//high-precision
int n;
struct node{
	int num[505],len;
	inline void clear(){
		memset(num,0,sizeof(num));
		len=0;
	}
	inline void print(){
		for(int i=len;i>=1;i--){
			printf("%d",num[i]);
		}
		printf("\n");
	}
	node operator + (const node &tmp){
		node res;
		res.clear();
		res.len=max(len,tmp.len)+1;
		for(int i=1;i<=res.len;i++){
			res.num[i]+=num[i]+tmp.num[i];
			if(res.num[i]>9){
				res.num[i+1]+=res.num[i]/10;
				res.num[i]%=10;
			}
		}
		while(res.num[res.len]) res.len++;
		while(!res.num[res.len]&&res.len>1) res.len--;
		return res;
	}
	node operator * (const node &tmp){
		node res;
		res.clear();
		res.len=len+tmp.len;
		for(int i=1;i<=len;i++){
			for(int j=1;j<=tmp.len;j++){
				res.num[i+j-1]+=num[i]*tmp.num[j];
				if(res.num[i+j-1]>9){
					res.num[i+j]+=res.num[i+j-1]/10;
					res.num[i+j-1]%=10;
				}
			}
		}
		while(res.num[res.len]) res.len++;
		while(!res.num[res.len]&&res.len>1) res.len--;
		return res;
	}
}a[105],dp[105][105],power[105],base;
inline node Max(node p,node q){
	if(p.len>q.len) return p;
	else if(p.len<q.len) return q;
	else{
		for(int i=p.len;i>=1;i--){
			if(p.num[i]>q.num[i]) return p;
			else if(p.num[i]<q.num[i]) return q;
		}
	}
	return p;
}
int main(){
	n=read();
	for(int i=1;i<=n;i++){
		a[i].clear();
	}
	for(int i=1;i<=n;i++){
		int tmp=read();
		if(!tmp){
			a[i].len=1,a[i].num[1]=0;
			continue;
		}
		while(tmp){
			a[i].num[++a[i].len]=tmp%10;
			tmp/=10;
		}
		//a[i].print();
	}
	base.len=1,base.num[1]=2;
	power[1].len=1,power[1].num[1]=2;
	for(int i=2;i<=n;i++){
		power[i]=power[i-1]*base;
		//power[i].print();
	}
	for(int i=1;i<=n;i++){
		dp[i][i]=a[i]*power[n];
	}
	for(int l=1;l<n;l++){
		for(int i=1,j=i+l;j<=n;i++,j=i+l){
			node ans1=a[i]*power[n-l],ans2=a[j]*power[n-l];
			ans1=ans1+dp[i+1][j],ans2=ans2+dp[i][j-1];
			dp[i][j]=Max(ans1,ans2);
		}
	}
	dp[1][n].print();
	return 0;
}

2.P1005 matrix access (disgusting version)

Because the answer of each line is actually independent, set a layer to enumerate the loop of each line and sum on the basis of the original question.

int n,m;
struct node{
	int num[505],len;
	inline void clear(){
		memset(num,0,sizeof(num));
		len=0;
	}
	inline void print(){
		for(int i=len;i>=1;i--){
			printf("%d",num[i]);
		}
		printf("\n");
	}
	node operator + (const node &tmp){
		node res;
		res.clear();
		res.len=max(len,tmp.len)+1;
		for(int i=1;i<=res.len;i++){
			res.num[i]+=num[i]+tmp.num[i];
			if(res.num[i]>9){
				res.num[i+1]+=res.num[i]/10;
				res.num[i]%=10;
			}
		}
		while(res.num[res.len]) res.len++;
		while(!res.num[res.len]&&res.len>1) res.len--;
		return res;
	}
	node operator * (const node &tmp){
		node res;
		res.clear();
		res.len=len+tmp.len;
		for(int i=1;i<=len;i++){
			for(int j=1;j<=tmp.len;j++){
				res.num[i+j-1]+=num[i]*tmp.num[j];
				if(res.num[i+j-1]>9){
					res.num[i+j]+=res.num[i+j-1]/10;
					res.num[i+j-1]%=10;
				}
			}
		}
		while(res.num[res.len]) res.len++;
		while(!res.num[res.len]&&res.len>1) res.len--;
		return res;
	}
}a[105][105],dp[105][105],power[105],base,ans;
inline node Max(node p,node q){
	if(p.len>q.len) return p;
	else if(p.len<q.len) return q;
	else{
		for(int i=p.len;i>=1;i--){
			if(p.num[i]>q.num[i]) return p;
			else if(p.num[i]<q.num[i]) return q;
		}
	}
	return p;
}
int main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			a[i][j].clear();
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			int tmp=read();
			if(!tmp){
				a[i][j].len=1,a[i][j].num[1]=0;
				continue;
			}
			while(tmp){
				a[i][j].num[++a[i][j].len]=tmp%10;
				tmp/=10;
			}
		}
	}
	base.len=1,base.num[1]=2;
	power[1].len=1,power[1].num[1]=2;
	for(int i=2;i<=m;i++){
		power[i]=power[i-1]*base;
	}
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=m;j++){
				dp[i][j].clear();
			}
		}
		for(int i=1;i<=m;i++){
			dp[i][i]=a[k][i]*power[m];
		}
		for(int l=1;l<m;l++){
			for(int i=1,j=i+l;j<=m;i++,j=i+l){
				node ans1=a[k][i]*power[m-l],ans2=a[k][j]*power[m-l];
				ans1=ans1+dp[i+1][j],ans2=ans2+dp[i][j-1];
				dp[i][j]=Max(ans1,ans2);
			}
		}
		ans=ans+dp[1][m];
	}
	ans.print();
	return 0;
}

3.P1006 NOIP2008 improve group pass slip

Very outrageous four-dimensional dp.

First, the maximum value that cannot be repeated from \ ((1,1) \) to \ ((n,m) \) and then from \ ((n,m) \) to \ ((1,1) \) is equivalent to the maximum value that cannot be repeated twice from \ ((1,1) \) to \ ((n,m) \), which is easier to consider.

Setting \ (dp(i,j,k,l) \) means going to \ ((i,j) \) for the first time and \ ((k,l) \) for the second time. Because it can only go down or right, it must be transferred from four situations, including:

\[dp(i,j,k,l)=\max(dp(i-1,j,k-1,l)dp(i-1,j,k,l-1),dp(i,j-1,k-1,l),dp(i,j-1,k,l-1))+a(i,j)+a(k,l) \]

Note that since the path cannot be repeated here, it is necessary to judge whether \ ((i,j) \) and \ ((k,l) \) are the same point.

Metaphysics \ (dp(n,m,n,m) \) is the final answer.

inline int Max(int a1,int a2,int a3,int a4){
	return max(max(a1,a2),max(a3,a4));
}
int main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			a[i][j]=read();
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			for(int k=n;k>=1;k--){
				for(int l=m;l>=1;l--){
					dp[i][j][k][l]=Max(dp[i-1][j][k-1][l],dp[i-1][j][k][l-1],dp[i][j-1][k-1][l],dp[i][j-1][k][l-1])+a[i][j];
					if(i!=k||j!=l) dp[i][j][k][l]+=a[k][l];
				}
			}
		}
	}
	printf("%d\n",dp[n][m-1][n-1][m]);
	return 0;
}

4.P1004 NOIP2000 improve group grid access

It's the same as passing a note

5.P1854 Florist window problem

The meaning of the question is to take a number from each line in the square of \ (n\times m \), and the horizontal and vertical numbers of the taken number are monotonically increasing to find the maximum value.

It is not hard to imagine that if \ (dp(i,j) \) means that the line \ (i \) is selected in \ ((i,j) \), then the transfer equation is:

\[dp(i,j)=\max_{k=i-1}^{j-1}\{dp(i-1,k)+a(i,j)\} \]

As for why the range of \ (k \) is \ ([i-1,j-1] \), the reason is that each line has to choose a position, so the \ (i-1 \) line should at least choose the position of \ ((i-1,i-1) \). As for the output path, use \ (nxt(i,j) \) to record the previous position and trace the output.

Pay attention to the range of loops in each layer, which can reduce meaningless operations, such as \ (i\in [1,n],j\in [i,m-n+i],k\in [i-1,j-1] \).

inline void print(int ord,int pos){
	if(ord==1){
		printf("%d ",pos);
		return;
	}
	print(ord-1,nxt[ord][pos]);
	printf("%d ",pos);
}
int main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			a[i][j]=read();
			dp[i][j]=minxn;
		}
	}
	for(int i=1;i<=n;i++){
		dp[0][i]=0;
	}
	for(int i=1;i<=n;i++){
		for(int j=i;j<=m-n+i;j++){
			for(int k=i-1;k<j;k++){
				if(dp[i-1][k]+a[i][j]>dp[i][j]){
					dp[i][j]=dp[i-1][k]+a[i][j];
					nxt[i][j]=k;
				}
			}
		}
	}
	for(int i=n;i<=m;i++){
		if(dp[n][i]>ans){
			ans=dp[n][i];
			last=i;
		}
	}
	printf("%d\n",ans);
	print(n,last);
	return 0;
}

6.P2690 Apple Catching G

In fact, it is no different from fetching in the 0-1 square of \ (n\times 2 \). Whether it is fetched depends on the result of the modulus of movement times \ (2 \).

int main(){
	t=read(),w=read();
	for(int i=1;i<=t;i++){
		a[i]=read();
	}
	for(int i=1;i<=t;i++){
		for(int j=0;j<=min(t,w);j++){
			if(!j){
				dp[i][j]=dp[i-1][j];
			}
			else{
				dp[i][j]=max(dp[i-1][j],dp[i-1][j-1]);
			}
			if(a[i]==j%2+1){
				dp[i][j]++;
			}
		}
	}
	for(int i=0;i<=w;i++){
		ans=max(ans,dp[t][i]);
	}
	printf("%d\n",ans);
	return 0;
}

4. Interval dp

Compared with the previous three types of DPS, the state transition is from front to back, that is, considering the contribution of the first \ (i \), the interval dp is more like the transition from small to large. Most states are set to \ (dp(i,j) \) to represent the interval \ ([i,j] \), and the interval is divided into two segments with \ (K \), namely \ ([i,k] \) and \ ([k+1,j] \).

Examples

1. Stone consolidation Simple version Regular Edition Enhanced version

First, the most basic transfer is

\[dp(i,j)=\max_{k=i}^{j-1}\{dp(i,k)+dp(k+1,j)\}+sum(i,j) \]

Maintain a prefix sum (the same is true for finding the minimum). If it is a ring, it is natural to copy \ ([1,n] \) for discussion.

Simple version

int n;
int a[305],sum[305];
int dp1[305][305],dp2[305][305];
int main(){
	n=read();
	for(int i=1;i<=n;i++){
		a[i]=read();
		sum[i]=sum[i-1]+a[i];
	}
	for(int l=1;l<n;l++){
		for(int i=1,j=i+l;j<=n;i++,j=i+l){
			dp1[i][j]=0x3f3f3f3f;
			for(int k=i;k<j;k++){ 
				dp1[i][j]=min(dp1[i][j],dp1[i][k]+dp1[k+1][j]+sum[j]-sum[i-1]);
				dp2[i][j]=max(dp2[i][j],dp2[i][k]+dp2[k+1][j]+sum[j]-sum[i-1]);
			}
		}
	}
	 
	printf("%d\n%d\n",dp1[1][n],dp2[1][n]);
	return 0;
}

Regular Edition

int main(){
	n=read();
	for(int i=1;i<=n;i++){
		a[i]=read();
		a[i+n]=a[i]; 
	}
	for(int i=1;i<=2*n;i++){
		sum[i]=sum[i-1]+a[i];
	} 
	for(int l=1;l<n;l++){
		for(int i=1,j=i+l;j<2*n;i++,j=i+l){
			dp1[i][j]=0x3f3f3f3f;
			for(int k=i;k<j;k++){ 
				dp1[i][j]=min(dp1[i][j],dp1[i][k]+dp1[k+1][j]+sum[j]-sum[i-1]);
				dp2[i][j]=max(dp2[i][j],dp2[i][k]+dp2[k+1][j]+sum[j]-sum[i-1]);
			}
		}
	}
	for(int i=1;i<=n;i++){
		ans1=min(ans1,dp1[i][i+n-1]);
		ans2=max(ans2,dp2[i][i+n-1]);
	}
	printf("%d\n%d\n",ans1,ans2);
	return 0;
}

The enhanced version is based on the \ (\ text {grassiawachs} \) algorithm. A perceptual understanding is that there are three piles of stones \ (a {I-1}, a I, a {I + 1} \), and the cost of the second merger must be \ (a {I-1} + a {I + 1} \), and the first merger must be related to \ (a_i \), so we only need to compare the size relationship between \ (a {I-1} \) and \ (a {I + 1} \).

3.P1018 the maximum product of noip2000 improvement group

Maintain a \ (sum(i,j) \) to represent the number of \ (s[i:j] \) parts, and use \ (dp(i,j) \) to represent the maximum product of \ (s[1:i] \) divided into \ (j \) parts. It is not difficult to get:

\[dp(i,j)=\max_{k=1}^{i}\{dp(k,j-1)\times sum(k+1,j)\} \]

If the output path is not very different from the linear one.

4.P1063 NOIP2006 increase group energy Necklace

First, we can see that a ring is formed. Naturally, we need to break the ring of \ (n \) into a chain of \ (n\times 2 \), and then follow the three-layer cycle of the classical interval dp - interval length - > interval starting point - > interval breakpoint. Finally, the answer is the maximum value of the interval with length of \ (n \).

int main(){
    n=read();
    for(int i=1;i<=n;i++){
        a[i]=read();
        a[n+i]=a[i];
    }
    for(int l=1;l<=n;l++){
        for(int i=1,j=i+l;i<=2*n&&j<=2*n;i++,j++){
            for(int k=i+1;k<=j-1;k++){
                dp[i][j]=max(dp[i][j],dp[i][k]+dp[k][j]+a[i]*a[j]*a[k]);
            }
        }
    }
    ll ans=0;
    for(int i=1;i<=n;i++){
       ans=max(ans,dp[i][i+n]);
    }
    printf("%lld",ans);
}

5.P4342 IOI1998 Polygon

The broken loop is still a chain, and the state settin g is the same. Use \ (f \) to represent the maximum value, and the addition operation is naturally \ (f (I, J) = \ max_ If there is a problem that the absolute value of F \ - K} is not equal to the minimum of the two sub \ {I \ + K}, there will be a problem that the maximum value of F \ - K} is not the product of the two absolute values of F \ - J \}.

Brain free metastasis simulates four combinations:

\[f(i,j)=\max_{k=i}^{j-1}\{max(f(i,k)\times(f(k+1,j),f(i,k)\times g(k+1,j),g(i,k)\times f(k+1,j),g(i,k)\times g(k+1,j))\} \]

\[g(i,j)=\min_{k=i}^{j-1}\{min(f(i,k)\times(f(k+1,j),f(i,k)\times g(k+1,j),g(i,k)\times f(k+1,j),g(i,k)\times g(k+1,j))\} \]

The output breakpoint of the second question only needs to traverse the \ ([i,i+n-1] \) that the answer matches.

6.P2890 Cheapest Palindrome G

It can be found that modifying a string into a palindrome string, deleting redundant characters and adding missing characters are actually equivalent, and have no impact on the subsequent answers. In fact, the cost of modification is the minimum value of increase and modification.

map<char,int> a;
int main(){
    n=read(),m=read();
    scanf("%s",s+1);
    for(int i=1;i<=n;i++){
        char ch;
        cin>>ch;
        int num1=read(),num2=read();
        a[ch]=min(num1,num2);
        //printf("%d\n",a[ch]);
    }
    memset(dp,0x3f,sizeof(dp));
    for(int i=1;i<=m;i++){
        dp[i][i]=0;
    }
    for(int l=1;l<m;l++){
        for(int i=1,j=i+l;j<=m;i++,j++){
            dp[i][j]=min(dp[i][j-1]+a[s[j]],dp[i+1][j]+a[s[i]]);
            if(s[i]==s[j]){
                if(l==1) dp[i][j]=0;
                else dp[i][j]=min(dp[i][j],dp[i+1][j-1]);
            }
            //printf("%d %d %d\n",i,j,dp[i][j]);
        }
    }
    printf("%d\n",dp[1][m]);
    return 0;
}

5. Tree dp

Now the structure as the background is transferred to the tree. The difference is that the previous linear dp traverses from front to back or from back to front, the interval dp traverses from small interval to large interval, and the tree dp traverses from leaf node to root node, which is similar to deep search.

Examples

1.P1040 additive binary tree

In fact, it is the interval dp. Because the middle order traversal is known, the root of \ ([l,r] \) must be within this range. Record the root node of each section and traverse the output according to the first order.

2.P2015 binary apple tree

Divide the subtree with \ (u \) root into two parts, then traverse and reserve several branches in the subtree currently judged, and take the maximum value.

3.P2014 course selection

ditto.

inline void add_edge(int u,int v){
    e[++cnt].to=v;
    e[cnt].nxt=head[u];
    head[u]=cnt;
}
inline void f(int u,int fa){
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        f(v,u);
        siz[u]+=siz[v]+1;
        for(int j=min(m,siz[u]);j>=1;j--){
            for(int k=min(j-1,siz[v]);k>=0;k--){
                dp[u][j]=max(dp[u][j],dp[u][j-k-1]+dp[v][k]+w[v]);
            }
        }
    }
}
int main(){
    n=read(),m=read();
    for(int i=1;i<=n;i++){
        int u=read();
        w[i]=read();
        add_edge(u,i);
        add_edge(i,u);
    }
    f(0,0);
    printf("%d\n",dp[0][m]);
    return 0;
}

4.P1352 dance without boss

The setting of status is related to whether to participate or not, that is \ (dp(u,0/1) \) indicates whether the root node contributes to the answer in the subtree with \ (u \) as the root, which is the maximum value of the answer. Set \ (G \) indicates the set of child nodes of node \ (u \), which can be obtained from the meaning of the question:

\[dp(u,0)=\max_{v\in G}\{dp(v,0),dp(v,1)\} \]

\[dp(u,1)=\max_{v\in G}\{dp(v,0)\}+w(u) \]

Output \ (\ max(dp(rt,0),dp(rt,1)) \).

inline void add_edge(int u,int v){
    e[++cnt].to=v;
    e[cnt].nxt=head[u];
    head[u]=cnt;
}
inline void f(int u,int fa){
    dp[u][0]=0,dp[u][1]=w[u];
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        f(v,u);
        dp[u][0]+=max(dp[v][0],dp[v][1]);
        dp[u][1]+=dp[v][0];
    }
}
int main(){
    n=read();
    for(int i=1;i<=n;i++){
        w[i]=read();
    }
    for(int i=1;i<n;i++){
        int u=read(),v=read();
        add_edge(u,v);
        add_edge(v,u);
        vis[u]=1;
    }
    for(int i=1;i<=n;i++){
        if(!vis[i]){
            rt=i;
            break;
        }
    }
    f(rt,0);
    printf("%d\n",max(dp[rt][0],dp[rt][1]));
    return 0;
}

5.Little fat guards the palace

As in the same question, the status settings of this question are divided into three \ (dp(u,0/1/2) \) which represent the following three situations respectively

  • The status \ (0 \) indicates that the node is guarded by itself.
  • Status \ (1 \) indicates that the node is guarded by child nodes.
  • The status \ (2 \) indicates that the node is guarded by the parent node, that is, it is not guarded when traversing the subtree.

The transition of state \ (0 \) and state \ (2 \) is relatively easy, because when the node is guarded by itself, the state of the child node has no impact, so there are:

\[dp(u,0)=\min_{v\in G}\{dp(v,0),dp(v,1),dp(v,2)\} \]

When the node is guarded by the parent node, if the child node is guaranteed to be guarded, the state of the child node can only be guarded. Therefore, there are:

\[dp(u,2)=\min_{v\in G}\{dp(v,0),dp(v,1)\} \]

The remaining state \ (1 \) is relatively complex, because it is necessary to ensure that at least one of all child nodes is transferred from state \ (0 \), which is essentially indistinguishable from state \ (2 \), so the transfer can be based on the answer of state \ (2 \).

It is easy to find that it will conflict with the condition if and only if \ (dp(v,0) > dp(v,1) \) is satisfied for any \ (v\in G \). Therefore, it only needs to traverse and process each \ (v \) to find out the smallest difference between \ (dp(v,0) \) and \ (dp(u,2) \) when \ (dp(v,1) \) is not better than \ (dp(v,1) \), that is:

\[dp(u,1)=\min_{v\in G}\{dp(u,2)-min(dp(v,0),dp(v,1))+dp(v,0)\} \]

If \ (dp(v,0) \) is taken, it naturally has no effect on the answer, so the state transition is correct.

inline void add_edge(int u,int v){
    e[++cnt].to=v;
    e[cnt].nxt=head[u];
    head[u]=cnt;
}
int dp[maxn][3];//0 himself, 1 son, 2 father
int rt;
inline void f(int u,int fa){
    dp[u][0]=w[u],dp[u][1]=maxxn,dp[u][2]=0;
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        f(v,u);
        dp[u][0]+=min(dp[v][0],min(dp[v][1],dp[v][2]));
        dp[u][2]+=min(dp[v][0],dp[v][1]);
    }
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dp[u][1]=min(dp[u][1],dp[u][2]-min(dp[v][0],dp[v][1])+dp[v][0]);
    }
}
int main(){
    n=read();
    for(int i=1;i<=n;i++){
        int u=read();
        w[u]=read();
        int siz=read();
        for(int j=1;j<=siz;j++){
            int v=read();
            add_edge(u,v);
            add_edge(v,u);
            vis[v]=1;
        }
    }
    for(int i=1;i<=n;i++){
        if(!vis[i]){
            rt=i;
            break;
        }
    }
    f(rt,0);
    printf("%d\n",min(dp[rt][0],dp[rt][1]));
    return 0;
}

6.P2585 ZJOI2006 three color binary tree

You only need to traverse the tree according to the first order, and then update it from top to bottom. Use \ (0 / 1 / 2 \) to represent three colors, one of which is transferred from the other two.

Secondary scanning and root replacement dp

Tree dp problems with uncertain roots.

First, a more direct solution is \ (O(n^2) \), which takes each node as the root node and runs once dp, but the complexity is extremely poor.

Classic idea: do a dp for the root node when it is \ (1 \), and then conduct a secondary scan to consider the impact of changing the root node on the answer, and update each answer.

7.P3478 POI2008 STA-Station/P2986 USACO10MAR Great Cow Gathering G

Two similar board questions.

First of all, the traversal of \ (dep(u),siz(u),dp(1) \) with \ (1 \) as the root node is very easy to do. I won't repeat it here. I'll mainly talk about the secondary scanning.

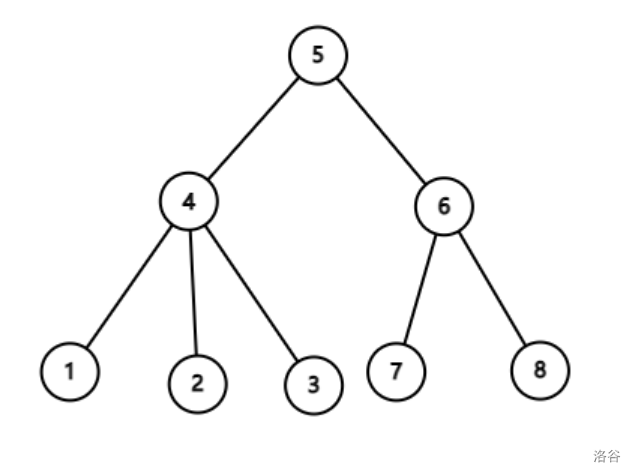
(select the root node with \ (5 \) as the initial node for beauty)

Considering the known \ (dp(5) \) transfer \ (dp(4) \), the sub tree depth with \ (4 \) as the root will be collective \ (- 1 \), and the other sub tree depth will be collective \ (+ 1 \), so:

\[dp(4)=dp(5)-siz(4)+(n-siz(4))=dp(5)+n-siz(4)\times \]

Generally speaking:

\[dp(v)=dp(u)+n-siz(v)\times 2 \]

Note the order of recursion and update in the second scan

inline void dfs(int u,int fa){
    dep[u]=dep[fa]+1,siz[u]=1;
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dfs(v,u);
        siz[u]+=siz[v];
    }
}
ll dp[maxn];
inline void secdfs(int u,int fa){
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dp[v]=dp[u]+n-2*siz[v];
        secdfs(v,u);
    }
}
ll ans=-1,pos;
int main(){
    n=read();
    for(int i=1;i<n;i++){
        int u=read(),v=read();
        add_edge(u,v);
        add_edge(v,u);
    }
    dfs(1,1);
    for(int i=1;i<=n;i++){
        dp[1]+=dep[i];
    }
    secdfs(1,1);
    for(int i=1;i<=n;i++){
        if(dp[i]>ans){
            ans=dp[i];
            pos=i;
        }
    }
    printf("%lld\n",pos);
    return 0;
}

For the second question, the only difference is that \ (siz(u) \) represents the number of cows, and it needs to be maintained that \ (wsiz(u) \) represents the cost, while the transfer equation during the second scan changes a little:

\[dp(v)=dp(u)+(siz(1)-siz(v)\times 2)\times w \]

At this time, the total number of cows is \ (siz(1) \), and the contribution to the answer is related to the weight.

Open longlong

8.P3047 Nearby Cows G

Use \ (dp(u,i) \) to indicate that the distance from the node \ (u \) is the sum of the node weights of \ (j \), then the first answer is \ (\ sum {I = 0} ^ {m} DP (1, I) \). Next, consider the secondary scan. It can be found that during the first update, the child node \ (v \) contributes to the parent node \ (u \), and the secondary scan is the contribution of the parent node \ (u \) to the child node \ (v \), Therefore, the original contribution of \ (v \) should be deleted first, and then \ (v \) should be modified. Pay attention to backtracking and order.

Changing dp is more and more like Mo team.

inline void dfs(int u,int fa){
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dfs(v,u);
        for(int j=1;j<=m;j++){
            dp[u][j]+=dp[v][j-1];
        }
    }
}
inline void secdfs(int u,int fa){
    for(int i=0;i<=m;i++){
        ans[u]+=dp[u][i];
    }
    for(int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        for(int j=1;j<=m;j++){
            dp[u][j]-=dp[v][j-1];
        }
        for(int j=1;j<=m;j++){
            dp[v][j]+=dp[u][j-1];
        }
        secdfs(v,u);
        for(int j=1;j<=m;j++){
            dp[v][j]-=dp[u][j-1];
        }
        for(int j=1;j<=m;j++){
            dp[u][j]+=dp[v][j-1];
        }
    }
}
int main(){
    n=read(),m=read();
    for(int i=1;i<n;i++){
        int u=read(),v=read();
        add_edge(u,v);
        add_edge(v,u);
    }
    for(int i=1;i<=n;i++){
        w[i]=read();
        dp[i][0]=w[i];
    }
    dfs(1,0);
    secdfs(1,0);
    for(int i=1;i<=n;i++){
        printf("%lld\n",ans[i]);
    }
    return 0;
}

9.CF708C Centroids

Problem solution

6. Digital dp

Waiting for change

7. Shape pressure dp

The core is to transfer each state \ (0-1 \) into decimal numbers when there are not many \ (n \).

Examples

1.P1896 SCOI2005 non aggression

Preprocess the situation that is legal for a single line, and then judge whether there are neighbors during transfer.

int n,m;
int sit[2005],sitcnt[2005],cnt;
inline void dfs(int sitk,int cntk,int pos){
    if(pos>=n){
        sit[++cnt]=sitk,sitcnt[cnt]=cntk;
        return;
    }
    dfs(sitk,cntk,pos+1);
    dfs(sitk|(1<<pos),cntk+1,pos+2);
}
ll dp[10][2005][105];//The status of the first i line is j, and the total number is k
ll ans=0;
int main(){
    n=read(),m=read();
    dfs(0,0,0);
    for(int i=1;i<=cnt;i++){
        dp[1][i][sitcnt[i]]=1;
    }
    for(int i=2;i<=n;i++){
        for(int j=1;j<=cnt;j++){
            for(int k=1;k<=cnt;k++){
                if(sit[j]&sit[k]) continue;
                if(sit[j]&(sit[k]<<1)) continue;
                if(sit[j]&(sit[k]>>1)) continue;
                for(int l=m;l>=sitcnt[j];l--){
                    dp[i][j][l]+=dp[i-1][k][l-sitcnt[j]];
                }
            }
        }
    }
    for(int i=1;i<=cnt;i++){
        ans+=dp[n][i][m];
    }
    printf("%lld\n",ans);
    return 0;
}

2.P2704 NOI2001 artillery position

The idea is the same as above, and the terrain needs to be pressed into a state

3.P2831 angry birds

Consider pressing the pigs currently knocked down into a state, and pressing the pigs that can be knocked down through a parabola at any two points into a state.

inline void get_ab(db &A,db &B,db a1,db a2,db b1,db b2,db c1,db c2){
    B=(a1*c2-a2*c1)/(a1*b2-a2*b1);
    A=(c1-b1*B)/a1;
}
int main(){
    t=read();
    for(int i=0;i<(1<<18);i++){
        int j;
        for(j=1;j<=18 && i&(1<<(j-1));j++);
        unbit[i]=j;
    }
    while(t--){
        memset(dp,0x3f,sizeof(dp));
        memset(para,0,sizeof(para));
        n=read(),m=read();
        for(int i=1;i<=n;i++){
            scanf("%lf%lf",&x[i],&y[i]);
        }
        dp[0]=0;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(fabs(x[i]-x[j])<eps) continue;
                db a,b;
                get_ab(a,b,x[i]*x[i],x[j]*x[j],x[i],x[j],y[i],y[j]);
                if(a>-eps) continue;
                for(int k=1;k<=n;k++){
                    if(fabs(a*x[k]*x[k]+b*x[k]-y[k])<eps){
                        para[i][j]|=(1<<(k-1));
                    }
                }
            }
        }
        for(int i=0;i<(1<<n);i++){
            int j=unbit[i];
            dp[i|(1<<(j-1))]=min(dp[i|(1<<(j-1))],dp[i]+1);
            for(int k=1;k<=n;k++){
                dp[i|para[j][k]]=min(dp[i|para[j][k]],dp[i]+1);
            }
        }
        printf("%d\n",dp[(1<<n)-1]);
    }
    return 0;
}

4.P3622 APIO2007 Zoo

Maintain whether each interval retains the contribution of animal state, and then enumerate the States to take the maximum value.

int main(){
    n=read(),m=read();
    for(int i=1;i<=m;i++){
        int e=read(),f=read(),l=read();
        int sitf=0,sitl=0;
        for(int j=1;j<=f;j++){
            int x=read();
            x=(x-e+n)%n;
            sitf|=(1<<x);
        }
        for(int j=1;j<=l;j++){
            int x=read();
            x=(x-e+n)%n;
            sitl|=(1<<x);
        }
        for(int j=0;j<=31;j++){
            if(sitf&(~j)||sitl&j){
                cnt[e][j]++;
            }
        }
    }
    for(int i=0;i<=31;i++){
        memset(dp[0],128,sizeof(dp[0]));
        dp[0][i]=0;
        for(int j=1;j<=n;j++){
            for(int s=0;s<=31;s++){
                dp[j][s]=max(dp[j-1][(s&15)<<1],dp[j-1][(s&15)<<1|1])+cnt[j][s];
            }
        }
        ans=max(ans,dp[n][i]);
    }
    printf("%d\n",ans);
    return 0;
}

Optimized dp

1. Monotone queue optimization dp

Monotone queue optimization = propose data independent of the inner loop, maintain the remaining problems related to the maximum and minimum with monotone queue, and require the transfer range to be sliding.

Examples

1.CF372C Watching Fireworks is Fun

Let \ (dp(i,j) \) represent the maximum value of the open center value obtained at the position \ (j \) when the \ (i \) th fireworks are released.

Let us set \ (dx=d\times (t_i-t_{i-1}) \), which represents the maximum distance that can be moved to \ (j \). It is not difficult to obtain the transfer equation:

\[dp(i,j)=\max_{k=j-dx}^{j+dx} \{dp(i-1,k)+b_i-|a_i-j|\} \]

Because the cumulative result of \ (b_i \) remains unchanged, it can be deleted from the transfer equation and added \ (sum_b \) to the result, which is simplified as follows:

\[dp(i,j)=\max_{k=j-dx}^{j=dx} \{dp(i-1,k)\}-|a_i-j| \]

Here, the result of \ (|a_i-j124\) is irrelevant to \ (k \), so it can be proposed. This value is actually negative, and the minimum value of its absolute value can be maintained. It is not difficult to find that each of our values is the most valuable one between \ ([j-dx,j+dx] \). Consider monotonic queue optimization.

You only need to do the following two operations:

  • The team leader element is currently the best and most advanced. If it is out of range, it needs to pop up
  • The tail element is probably the best, and finally, if there are no new entrants, they need to pop up

However, our monotone queue can only support the range of \ (j \), so we split this range and run the pros and cons respectively.

int main(){
    n=read(),m=read(),d=read();
    memset(dp,0x3f,sizeof(dp));
    for(int i=1;i<=m;i++){
        a[i]=read(),b[i]=read(),t[i]=read();
        sum+=b[i];
    }
    for(int i=1;i<=n;i++){
        dp[1][i]=Abs(a[1]-i);
    }
    for(int i=2;i<=m;i++){
        ll dx=(t[i]-t[i-1])*d;
        memset(dp[i&1],0x3f,sizeof(dp[i&1]));
        head=1,tail=0;
        for(int j=1;j<=n;j++){
            while(head<=tail&&q[head]<j-dx) head++;
            while(head<=tail&&dp[i&1^1][q[tail]]>dp[i&1^1][j]) tail--;
            q[++tail]=j;
            dp[i&1][j]=Min(dp[i&1][j],dp[i&1^1][q[head]]+Abs(a[i]-j));
        }
        head=1,tail=0;
        for(int j=n;j>=1;j--){
            while(head<=tail&&q[head]>j+dx) head++;
            while(head<=tail&&dp[i&1^1][q[tail]]>dp[i&1^1][j]) tail--;
            q[++tail]=j;
            dp[i&1][j]=Min(dp[i&1][j],dp[i&1^1][q[head]]+Abs(a[i]-j));
        }
    }
    ans=0x3f3f3f3f3f3f3f3f;
    for(int i=1;i<=n;i++){
        ans=Min(ans,dp[m&1][i]);
    }
    printf("%lld\n",sum-ans);
    return 0;
}

2.P2569 SCOI2010 stock trading

Naturally \ (dp(i,j) \) represents the highest return of holding \ (j \) stocks on the \ (i \) day. It is not difficult to find three states: no operation, buy and sell.

The transfer without operation is very simple, \ (dp(i,j)=\max(dp(i,j),dp(i-1,j)) \)

In fact, there is no need to enumerate \ (i-w-1 \) and the previous days for the trading operation, because the non operation has been transferred to the next day, so it is enough to transfer from \ (dp(i-w-1,k) \), and two transfer equations can be obtained.

Buy:

\[dp(i,j)=\max_{k=j-as_i}^{j-1}\{dp(i-w-1,k)-ap_i\times (j-k)\} \]

It is proposed that the item independent of \ (k \) is obtained:

\[dp(i,j)=\max_{k=j-as_i}^{j-1}\{dp(i-w-1,k)+ap_i\times k\}-ap_i\times j \]

Sell:

\[dp(i,j)=\max_{j+1}^{j+bs_i}\{dp(i-w-1,k)+bp_i\times(k-j)\} \]

Similarly, by simplifying, we can get:

\[dp(i,j)=\max_{j+1}^{j+bs_i}\{dp(i-w-1,k)+bp_i\times k\}-bp_i\times j \]

Obviously, the in parentheses can be optimized with monotone queue.

int main(){
    n=read(),m=read(),w=read();
    for(int i=1;i<=n;i++){
        ap[i]=read(),bp[i]=read(),as[i]=read(),bs[i]=read();
    }
    memset(dp,~0x3f,sizeof(dp));
    for(int i=0;i<=n;i++){
        dp[i][0]=0;
    }
    for(int i=1;i<=n;i++){
        for(int j=0;j<=as[i];j++){
            dp[i][j]=-1*j*ap[i];
        }
        for(int j=0;j<=m;j++){
            dp[i][j]=max(dp[i][j],dp[i-1][j]);
        }
        if(i>=w+1){
            head=1,tail=0;
            for(int j=0;j<=m;j++){
                while(head<=tail&&q[head]<j-as[i]) head++;
                while(head<=tail&&dp[i-w-1][j]+ap[i]*j>=dp[i-w-1][q[tail]]+ap[i]*q[tail]) tail--;
                q[++tail]=j;
                if(head<=tail) dp[i][j]=max(dp[i][j],dp[i-w-1][q[head]]-ap[i]*(j-q[head]));
            }
            head=1,tail=0;
            for(int j=m;j>=0;j--){
                while(head<=tail&&q[head]>j+bs[i]) head++;
                while(head<=tail&&dp[i-w-1][j]+bp[i]*j>=dp[i-w-1][q[tail]]+bp[i]*q[tail]) tail--;
                q[++tail]=j;
                if(head<=tail) dp[i][j]=max(dp[i][j],dp[i-w-1][q[head]]+bp[i]*(q[head]-j));
            }
        }
    }
    int ans=-1;
    for(int i=0;i<=m;i++){
        ans=max(ans,dp[n][i]);
    }
    printf("%d\n",ans);
    return 0;
}

3.P2254 NOI2005 magnificent Waltz

Ignoring the starting position and so on, each interval optimizes p with monotone queue d for each row or column in the whole map, and scrolls the array to reduce space.

4.P2627 Mowing the Lawn G

\[dp_i=\max_{k=i-k}^{i}\{dp_{j-1}+sum_i-sum_j\} \]

\[dp_i=\max_{k=i-k}^{i}\{dp_{j-1}-sum_j\}+sum_i \]

Conventional monotonic queue optimization is sufficient.

2. Slope optimization dp

It's really hard to optimize.

To put it simply: when there is a formula in the form of \ (a[i]\times b[j]+c[i]+d[j] \) in the recursive formula, it is obvious that monotone queue optimization is not feasible. Therefore, we can get a convex hull in the form of a function \ (b=y-kx \), and use monotone queue to maintain the convex hull.

Examples

1.P3195 HNOI2008 toy packing

First find the prefix sum \ (pre \), and you can directly get the recursive formula: \ (dp_i=\min_{j=1}^{i-1}\{dp_j+(pre_i-pre_j+i-j-1-l)^2 \} \)

Let \ (sum_i=pre_i+1,l'=l+1 \), for the convenience of observation, remove \ (\ min \), and you can get \ (dp_i=dp_j+(sum_i-sum_l-l')^2 \), which also includes: \ (dp_i=dp_j+sum_i^2+(sum_j+l')^2-2sum_isum_j-2sum_il '\), and then move the item to the above formula to have \ (dp_i-sum_i^2+2sum_il'=dp_j+(sum_j+l')^2-2sum_i\times sum_j \), where \ (b=dp_i-sum_i^2+2sum_il',y=dp_j+(sum_j+l')^2,k=2sum_i,x=sum_j\).

Then we get a lower convex hull, let the slope be as small as possible under the condition that it is guaranteed to be greater than \ (k \), and the monotone queue maintains this convex hull.

ll n,l;
ll sum[maxn],dp[maxn];
ll q[maxn],head,tail;
inline ll X(ll i){
    return sum[i];
}
inline ll Y(ll i){
    return dp[i]+(sum[i]+l)*(sum[i]+l);
}
inline ldb slope(ll i,ll j){
    return (ldb)(Y(j)-Y(i))/(X(j)-X(i));
}
int main(){
    n=read(),l=read()+1;
    for(int i=1;i<=n;i++){
        sum[i]=read()+sum[i-1]+1;
    }
    head=1,tail=1;
    q[1]=0;
    for(int i=1;i<=n;i++){
        while(head<tail&&slope(q[head],q[head+1])<=2*sum[i]) head++;
        dp[i]=dp[q[head]]+(sum[i]-sum[q[head]]-l)*(sum[i]-sum[q[head]]-l);
        while(head<tail&&slope(q[tail-1],q[tail])>=slope(q[tail-1],i)) tail--;
        q[++tail]=i;
    }
    printf("%lld\n",dp[n]);
    return 0;
}

2.P3628 APIO2010 special task force

Let's talk about the conventional practice of slope optimization.

The first thing is to maintain the prefix and \ (sum \ \). The first thing to do is to maintain the prefix and the prefix and \ (sum \ \). The normal recursive formula (omitted \ (\ min \)) is \ (dp_u u u u u j + a (sum u u u u u u u u u u u u u u u u u u u u u u u u j + C \). We open the formula, and move the relevant of \ (I \) to the left side of the equation, and we can get \ (dp_i I I = u i = dp_i = dp_i = dp_i = dp_i = dp_i = u i = u u uuu u u j j + j + asum_j + C \). The normal recursive formula (omitted \ (\\\omitted \ (\ omitted \ (\ \\j ^ 2-bsum_ (j + C \), In this way, we get the recurrence formula in the form of \ (b=y-kx \). We can find that our \ (B \) is about \ (I \), \ (Y \) is about \ (J \) \ (- KX \) is a term related to \ (i,j \), and the first half is regarded as \ (- k \) and the second half as \ (x \).

After that, you only need to bring in the maintenance convex hull.

int n;
int a,b,c;
ll sum[maxn],dp[maxn];
int q[maxn],head,tail;
inline ll X(int i){
    return sum[i];
}
inline ll Y(int i){
    return dp[i]+a*sum[i]*sum[i]-b*sum[i];
}
inline ll K(int i){
    return 2*a*sum[i];
}
inline ll B(int i){
    return dp[i]-a*sum[i]*sum[i]-b*sum[i]-c;
}
inline db slope(int i,int j){
    return (db)(Y(i)-Y(j))/(X(i)-X(j));
}
int main(){
    n=read();
    a=read(),b=read(),c=read();
    for(int i=1;i<=n;i++){
        sum[i]=sum[i-1]+read();
    }
    int head=1,tail=1;
    q[tail]=0;
    for(int i=1;i<=n;i++){
        while(head<tail&&slope(q[head],q[head+1])>K(i)) head++;
        dp[i]=Y(q[head])-K(i)*X(q[head])+a*sum[i]*sum[i]+b*sum[i]+c;
        while(head<tail&&slope(q[tail-1],q[tail])<=slope(q[tail],i)) tail--;
        q[++tail]=i;
    }
    printf("%lld\n",dp[n]);
    return 0;
}

3.P2120 ZJOI2007 warehouse construction

It is also a few steps - prefix and - pusher - shift sorting - maintaining convex shell.

3. Quadrilateral inequality optimization dp

Waiting for change

Added by miltonbanks on Thu, 03 Feb 2022 17:38:14 +0200

Popular Keywords

©2025 Programming VIP