Introduction to Numpy Library

NumPy is a powerful Python library, which is mainly used to perform calculations on multidimensional arrays. The word NumPy comes from two words -- Numerical and python. NumPy provides a large number of library functions and operations to help programmers easily perform Numerical calculations. It is widely used in the field of data analysis and machine learning. It has the following characteristics:

1. Numpy has built-in parallel computing function. When the system has multiple cores, numpy will automatically perform parallel computing when doing some computing.
2. The bottom layer of Numpy is written in C language, and the GIL (global interpreter lock) is released internally. Its operation speed on the array is not limited by the Python interpreter, and its efficiency is much higher than that of pure Python code.
3. There is a powerful N-dimensional Array object Array (something similar to a list).
4. Practical linear algebra, Fourier transform and random number generation function.

Performance comparison between Numpy array and Python list:

For example, we want to square each element in a Numpy array and Python list. Then the code is as follows:
python list:

import numpy as np
import time
t1=time.time()
a=[]
for x in range(1000000):
    a.append(x**2)
t2=time.time()
print('python List time consuming:',t2-t1)

result:

python List time consuming: 0.34757137298583984

numpy array:

t3=time.time()
b=np.arange(1000000)**2
t4=time.time()
print('numpy Array time consuming:',t4-t3)

result:

numpy Array time consuming: 0.003968954086303711

Tutorial address:

Official website: https://docs.scipy.org/doc/numpy/user/quickstart.html .
Chinese documents: https://www.numpy.org.cn/user_guide/quickstart_tutorial/index.html .

catalog:

• Basic usage of Numpy array
• Numpy array operation
• Numpy index and slice
• Deep copy and shallow copy
• File operation
• NAN and INF value processing
• np.random module
• Axis understanding
• General function

Basic usage of NumPy array

• Numpy is a Python scientific computing library used to quickly process arrays of arbitrary dimensions.
• Numpy provides an N-dimensional array type ndarray, which describes a collection of "items" of the same type.
• Numpy.ndarray supports vectorization.
• Numpy is written in c language, and the GIL is released at the bottom. Its operation speed on the array is no longer limited by the python interpreter.

Array in numpy:

The use of arrays in Numpy is very similar to lists in Python. The differences between them are as follows:

1. Multiple data types can be stored in a list. For example, a = [1, 'a'] is allowed, while arrays can only store the same data type.
2. Arrays can be multidimensional. When all the data in multidimensional arrays are numerical types, they are equivalent to matrices in linear algebra and can operate on each other.

Create an array (np.ndarray object):

The data type of the array in Numpy is called ndarray.

1. Generated from lists in Python:

import numpy as np
a1 = np.array([1,2,3,4])
print(a1)
print(type(a1))

1. Use NP Arange generation, NP The usage of range is similar to that of range in Python:

import numpy as np
a2 = np.arange(2,21,2)
print(a2)

1. Use NP Random generates an array of random numbers:

a1 = np.random.random(2,2) # Generates an array of random numbers with 2 rows and 2 columns
a2 = np.random.randint(0,10,size=(3,3)) # The element is a random array of 3 rows and 3 columns from 0 to 10

1. Use the function to generate a special array:

import numpy as np
a1 = np.zeros((2,2)) #Generate an array of 2 rows and 2 columns with all elements of 0
a2 = np.ones((3,2)) #Generate an array of 3 rows and 2 columns with all elements being 1
a3 = np.full((2,2),8) #Generate an array of 2 rows and 2 columns with all elements of 8
a4 = np.eye(3) #Generate a 3x3 matrix with element 1 and other elements 0 on the skew square

Common properties of ndarray:

ndarray.dtype:

Because the array can only store the same data type, you can get the data type of the elements in the array through dtype. Here is ndarray Common data types of dtype:

data type	describe	Unique identifier
bool	Boolean type (True or False) stored in one byte	'b'
int8	One byte size, - 128 to 127	'i1'
int16	Integer, 16 bit integer (- 32768 ~ 32767)	'i2'
int32	Integer, 32-bit integer (- 2147483648 ~ 2147483647)	'i4'
int64	Integer, 64 bit integer (- 9223372036854775808 ~ 9223372036854775807)	'i8'
uint8	Unsigned integer, 0 to 255	'u1'
uint16	Unsigned integer, 0 to 65535	'u2'
uint32	Unsigned integer, 0 to 2 * * 32 - 1	'u4'
uint64	Unsigned integer, 0 to 2 * * 64 - 1	'u8'
float16	Semi precision floating point number: 16 bits, sign 1 bit, index 5 bits, precision 10 bits	'f2'
float32	Single precision floating point number: 32 bits, sign 1 bit, exponent 8 bits, precision 23 bits	'f4'
float64	Double precision floating point number: 64 bits, sign 1 bit, index 11 bits, precision 52 bits	'f8'
complex64	Complex number, which represents the real part and imaginary part with two 32-bit floating-point numbers respectively	'c8'
complex128	Complex numbers, representing the real part and imaginary part with two 64 bit floating-point numbers respectively	'c16'
object_	python object	'O'
string_	character string	'S'
unicode_	unicode type	'U'

We can see that Numpy has many more types of values than Python's built-in, because Numpy is designed to efficiently process massive data. For example, if you want to store tens of billions of numbers, and these numbers do not exceed 254 (within a byte), you can set dtype to int8, which can save memory space more than using int64 by default. The type related operations are as follows:

1. default data type

import numpy as np
a=np.arange(10)
print(a)
print(a.dtype)
# If it is a windows system, the default is int32
# If it is a mac or linux system, it is determined according to the system

result:

[0 1 2 3 4 5 6 7 8 9]
int32

1. Specify the data type for each element

b=np.array([1,2,3,4,5],dtype=np.int8)#Specify the type of each element
print(b)
print(b.dtype)

result:

[1 2 3 4 5]
int8

f=np.array(['a','b'],dtype='S')#Unique identifier of string'S'
print(f)
print(f.dtype)

result:

[b'a' b'b']
|S1

1. Storage object

class Person:
    def __init__(self,name,age):
        self.name=name
        self.age=age
d=np.array([Person('Zhang San',18),Person('Li Si',18)])
print(d)
print(d.dtype)

result:

[<__main__.Person object at 0x000001B757D7CEE0>
 <__main__.Person object at 0x000001B757D7C910>]
object

1. Modify the data type of each element

import numpy as np
a1 = np.array([1,2,3])
print(a1.dtype) # In the window system, the default is int32
# Modify dtype below
a2 = a1.astype(np.int64) # astype does not modify the array itself, but returns the modified result
print(a2.dtype)

result:

int32
int64

ndarray.size: get the number of elements of the array

import numpy as np
   a1 = np.array([[1,2,3],[4,5,6]])
   print(a1.size) #6 is printed because there are a total of 6 elements

ndarray.ndim: Dimension of array

 a1 = np.array([1,2,3])
   print(a1.ndim) # Dimension is 1
   a2 = np.array([[1,2,3],[4,5,6]])
   print(a2.ndim) # Dimension is 2
   a3 = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
   print(a3.ndim) # Dimension is 3

ndarray.shape:

The array created by numpy has a shape attribute, which is a tuple and returns the dimension of each dimension. Sometimes we may need to know the specific dimension of a certain dimension.

Code example 1:

 a1 = np.array([1,2,3])
   print(a1.shape) # Output (3,), which means a one-dimensional array with 3 data

   a2 = np.array([[1,2,3],[4,5,6]])
   print(a2.shape) # Output (2,3), which means a binary array, 2 rows and 3 columns

   a3 = np.array([
       [
           [1,2,3],
           [4,5,6]
       ],
       [
           [7,8,9],
           [10,11,12]
       ]
   ])
   print(a3.shape) # Output (2,2,3), which means a three-dimensional array. There are two blocks in total, and each element has two rows and three columns

Code example 2:

Two dimensional case
>>> import numpy as np
>>> y = np.array([[1,2,3],[4,5,6]])
>>> print(y)
[[1 2 3]
 [4 5 6]]
>>> print(y.shape)
(2, 3)
>>> print(y.shape[0])
2
>>> print(y.shape[1])
3
 Can see y Is a two-dimensional array with two rows and three columns, y.shape[0]Number of representative lines, y.shape[1]Represents the number of columns.

Three dimensional situation
>>> x  = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[0,1,2]],[[3,4,5],[6,7,8]]])
>>>> print(x)
[[[1 2 3]
  [4 5 6]]

 [[7 8 9]
  [0 1 2]]

 [[3 4 5]
  [6 7 8]]]
>>> print(x.shape)
(3, 2, 3)
>>> print(x.shape[0])
3
>>> print(x.shape[1])
2
>>> print(x.shape[2])
3
 Can see x It is a three-dimensional array containing three two-dimensional arrays with two rows and three columns, x.shape[0]Represents the number of two-dimensional arrays, x.shape[1]Represents the number of rows of a two-dimensional array, x.shape[2]Represents the number of columns in a two-dimensional array.

summary
 As you can see, shape[0]Represents the dimension of the outermost array, shape[1]Represents the dimension of the sub peripheral array. The number is increasing and the dimension is from outside to inside.

In addition, we can also use ndarray Reshape to modify the dimension of the array. The example code is as follows:

 a1 = np.arange(12) #Generate a one-dimensional array with 12 data
   print(a1) 

   a2 = a1.reshape((3,4)) #It becomes a two-dimensional array with 3 rows and 4 columns
   print(a2)

   a3 = a1.reshape((2,3,2)) #Into a three-dimensional array, a total of 2 blocks, each block is 2 rows and 2 columns
   print(a3)

   a4 = a2.reshape((12,)) # Change the two-dimensional array of a2 into a one-dimensional array with 12 columns, (12,) indicates that the tuple needs to be left blank when there is only one value
   print(a4)

   a5 = a2.flatten() # No matter how many dimensions a2 is, it will become a one-dimensional array
   print(a5)

Brief summary:

• reshape(1,12) # changes to a two-dimensional array. reshape() can be understood as an array with several parameters
• Several elements in the shape result represent several dimensional arrays

ndarray.itemsize:

The size of each element in the array, in bytes. For example, the following code:

   a1 = np.array([1,2,3],dtype=np.int32)
   print(a1.itemsize) # Print 4, because each byte is 8 bits, 32 bits / 8 = 4 bytes

Numpy array operation

Calculation of arrays and numbers:

In the Python list, if you want to add a number to all the elements in the list, you can either use the map function or loop the whole list. However, the array in NumPy can be operated directly on the array. The example code is as follows:

import numpy as np
a1 = np.random.random((3,4))
print(a1)
# If you want to multiply all elements on the a1 array by 10, you can do so by
a2 = a1*10#Grammar sugar
print(a2)
# You can also use round to keep only 2 decimal places for all elements
a3 = a2.round(2)

The above example is multiplication. In fact, addition, subtraction and division are similar.

Array and array calculation:

Related operations between corresponding elements:

import numpy as np
a1 = np.arange(0,24).reshape((3,8))
a2 = np.random.randint(1,10,size=(3,8))
a3 = a1 * a2 #Addition / subtraction / division / multiplication can be related to the elements in the corresponding position
print(a1)
print(a2)
print(a3)

result:

[[ 0  1  2  3  4  5  6  7]
 [ 8  9 10 11 12 13 14 15]
 [16 17 18 19 20 21 22 23]]
[[5 8 7 1 3 3 8 5]
 [1 2 4 3 7 5 3 8]
 [1 7 2 4 1 3 3 4]]
[[  0   8  14   3  12  15  48  35]
 [  8  18  40  33  84  65  42 120]
 [ 16 119  36  76  20  63  66  92]]

Operations between arrays with the same number of rows and only 1 column:

import numpy as np
a1 = np.random.randint(10,20,size=(3,8)) #3 rows and 8 columns
a2 = np.random.randint(1,10,size=(3,1)) #3 rows and 1 column
a3 = a1 - a2 #The number of rows is the same, and a2 has only one column, which can operate on each other
print(a1)
print('='*30)
print(a2)
print('='*30)
print(a3)

result:

[[11 17 14 14 16 19 11 16]
 [10 14 15 10 18 11 19 10]
 [19 19 18 17 17 18 18 10]]
==============================
[[4]
 [3]
 [1]]
==============================
[[ 7 13 10 10 12 15  7 12]
 [ 7 11 12  7 15  8 16  7]
 [18 18 17 16 16 17 17  9]]

It is not difficult to find that each element of each column of a1 subtracts the value of each element corresponding to a2

Operations between arrays with the same number of columns and only 1 row:

import numpy as np
a1 = np.random.randint(10,20,size=(3,8)) #3 rows and 8 columns
a2 = np.random.randint(1,10,size=(1,8))
a3 = a1 - a2
print(a1)
print('='*30)
print(a2)
print('='*30)
print(a3)

result:

[[19 10 10 10 19 11 16 11]
 [10 17 10 13 17 18 10 15]
 [14 10 14 11 16 18 15 17]]
==============================
[[2 4 1 9 6 3 3 8]]
==============================
[[17  6  9  1 13  8 13  3]
 [ 8 13  9  4 11 15  7  7]
 [12  6 13  2 10 15 12  9]]

It is not difficult to find that each element of each row of a1 subtracts the value of each element corresponding to a2

Broadcasting principle:

If the axis lengths of the trailing dimension (i.e. the dimension from the end) of the two arrays match, or the length of one of them is 1, they are considered broadcast compatible. Broadcasting will be carried out on the missing and / or length 1 dimensions. See the following case analysis:

1. Can an array with shape of (3,8,2) operate with an array of (8,3)?
   Analysis: No, because according to the broadcasting principle, 2 and 3 in (3,8,2) and (8,3) are not equal from the back to the front, so the operation cannot be carried out.

2. Can an array with shape of (3,8,2) operate with an array of (8,1)?
   Analysis: Yes, because according to the broadcasting principle, although 2 and 1 in (3,8,2) and (8,1) are not equal, one side can participate in the operation because its length is 1.

3. Can an array with shape of (3,1,8) operate with an array of (8,1)?
   Analysis: Yes, because according to the broadcasting principle, 4 and 1 in (3,1,4) and (8,1) are not equal and 1 and 8 are not equal, but one of the two terms has a length of 1, so it can participate in the operation.

Code example:

a1=np.array([1,2,3,4])
a2=np.random.randint(1,10,size=(8,1))
a3=a1+a2
print(a1)
print('='*30)
print(a2)
print('='*30)
print(a3)
print('='*30)
print(a3.shape)

result:

[1 2 3 4]
==============================
[[7]
 [1]
 [7]
 [2]
 [8]
 [1]
 [6]
 [3]]
==============================
[[ 8  9 10 11]
 [ 2  3  4  5]
 [ 8  9 10 11]
 [ 3  4  5  6]
 [ 9 10 11 12]
 [ 2  3  4  5]
 [ 7  8  9 10]
 [ 4  5  6  7]]
==============================
(8, 4)

Operation of array shape:

Through some functions, it is very convenient to operate the shape of the array.

reshape and resize methods:

1. reshape is to convert the array into a specified shape, and then return the converted result. The shape of the original array will not change. Call method:

a1 = np.random.randint(0,10,size=(3,4))
a2 = a1.reshape((2,6)) #Return the modified result without affecting the original array itself

1. resize is to convert the array into a specified shape, which will directly modify the array itself. No value is returned. Call method:

a1 = np.random.randint(0,10,size=(3,4))
a1.resize((2,6)) #a1 itself has changed

flatten and t ravel methods:

Both methods convert multi-dimensional arrays into one-dimensional arrays, but there are the following differences:

• flatten converts the array into a one-dimensional array and then returns the copy back, so subsequent modifications to the return value will not affect the previous array.
• T ravel returns the view (which can be understood as a reference) after converting the array into a one-dimensional array, so subsequent modifications to the return value will affect the previous array.

x = np.array([[1, 2], [3, 4]])
x.flatten()[1] = 100 #At this time, the position element of x[0] is still 1
x.ravel()[1] = 100 #At this time, the position element of x[0] is 100

Combination of different arrays:

If you want to combine multiple arrays, you can also use some of these functions.

1. vstack: stack arrays vertically. The array must have the same number of columns to stack. The example code is as follows:

a1 = np.random.randint(0,10,size=(3,5))
a2 = np.random.randint(0,10,size=(1,5))
a3 = np.vstack([a1,a2])

1. Hsstack: stack arrays horizontally. The rows of the array must be the same to overlay. The example code is as follows:

a1 = np.random.randint(0,10,size=(3,2))
a2 = np.random.randint(0,10,size=(3,1))
a3 = np.hstack([a1,a2])

3.concatenate([],axis): stack two arrays, but in the horizontal or vertical direction. It depends on the parameters of axis. If axis=0, If axis=1, then it means stacking in the vertical direction (row). If axis=None, then the two arrays will be combined into a one-dimensional array. It should be noted that if stacking in the horizontal direction, then the rows must be the same. If stacking in the vertical direction, then the columns must be the same. The example code is as follows:

a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6]])
np.concatenate((a, b), axis=0)
# result:
array([[1, 2],
    [3, 4],
    [5, 6]])

np.concatenate((a, b.T), axis=1)
# result:
array([[1, 2, 5],
    [3, 4, 6]])

np.concatenate((a, b), axis=None)
# result:
array([1, 2, 3, 4, 5, 6])

Cutting of array:

Through hsplit, vsplit and array_split can cut an array.

1. hsplit: cut in the vertical direction. It is used to specify how many columns are divided. You can use numbers to represent how many parts are divided, or you can use arrays to represent where to divide. The example code is as follows:

a1 = np.arange(16.0).reshape(4, 4)
np.hsplit(a1,2) #Split into two parts
>>> array([[ 0.,  1.],
     [ 4.,  5.],
     [ 8.,  9.],
     [12., 13.]]), array([[ 2.,  3.],
     [ 6.,  7.],
     [10., 11.],
     [14., 15.]])]

np.hsplit(a1,[1,2]) #It means cutting a knife where the subscript is 1 and cutting a knife where the subscript is 2. It is divided into three parts
>>> [array([[ 0.],
     [ 4.],
     [ 8.],
     [12.]]), array([[ 1.],
     [ 5.],
     [ 9.],
     [13.]]), array([[ 2.,  3.],
     [ 6.,  7.],
     [10., 11.],
     [14., 15.]])]

1. vsplit: cut horizontally. It is used to specify how many lines to divide. You can use numbers to represent how many parts to divide, or you can use arrays to represent where to divide. The example code is as follows:

np.vsplit(x,2) #Represents a total of 2 arrays divided into rows
>>> [array([[0., 1., 2., 3.],
     [4., 5., 6., 7.]]), array([[ 8.,  9., 10., 11.],
     [12., 13., 14., 15.]])]

np.vsplit(x,(1,2)) #Delegates are divided by row, where the subscript is 1 and where the subscript is 2
>>> [array([[0., 1., 2., 3.]]),
    array([[4., 5., 6., 7.]]),
    array([[ 8.,  9., 10., 11.],
           [12., 13., 14., 15.]])]

1. split/array_ Split (array, indicate_or_secont, axis): used to specify the cutting method. When cutting, you need to specify whether to cut by row or column. axis=1 represents by column and axis=0 represents by row. The example code is as follows:

np.array_split(x,2,axis=0) #Cut into 2 parts in vertical direction
>>> [array([[0., 1., 2., 3.],
     [4., 5., 6., 7.]]), array([[ 8.,  9., 10., 11.],
     [12., 13., 14., 15.]])]

Array (matrix) transpose and axis swap:

An array in numpy is actually a matrix in linear algebra. Matrices can be transposed. ndarray has a T attribute that returns the result of the transpose of this array. The example code is as follows:

a1 = np.arange(0,24).reshape((4,6))
a2 = a1.T
print(a2)

Another method is called transfer. This method returns a View (which can be understood as a reference temporarily), that is, modifying the return value will affect the original array. The example code is as follows:

a1 = np.arange(0,24).reshape((4,6))
a2 = a1.transpose()

Why do we need to transpose the matrix? Sometimes we need to use it when doing some calculations. For example, when doing the inner product of a matrix. The matrix must be transposed and multiplied by the previous matrix:

a1 = np.arange(0,24).reshape((4,6))
a2 = a1.T
print(a1)
print('='*30)
print(a2)
print('='*30)
print(a1.dot(a2))#The dot function returns the inner product of two matrices

result:

[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]
 [12 13 14 15 16 17]
 [18 19 20 21 22 23]]
==============================
[[ 0  6 12 18]
 [ 1  7 13 19]
 [ 2  8 14 20]
 [ 3  9 15 21]
 [ 4 10 16 22]
 [ 5 11 17 23]]
==============================
[[  55  145  235  325]
 [ 145  451  757 1063]
 [ 235  757 1279 1801]
 [ 325 1063 1801 2539]]

Numpy index and slice:

1. Operations on one-dimensional arrays:

import numpy as np
#One dimensional array (same usage as python list slicing)
a1=np.arange(10)#Generate a 1-9 one-dimensional array
print(a1)
#Index operation
print(a1[4])
#Slice operation
print(a1[4:6])

result:

[0 1 2 3 4 5 6 7 8 9]
4
[4 5]

1. Multidimensional array

Indexes and slices. Indexes are discontinuous and slices are continuous. If commas are used for separation, rows are in front of commas and columns are behind commas. If only one value in multidimensional array is a row (brackets need to be added), slices do not need brackets.

import numpy as np
a2=np.random.randint(0,10,size=(4,6))
print(a2)

result:

[[4 9 9 0 0 9]
 [2 4 4 5 2 0]
 [9 5 4 0 8 5]
 [8 2 3 3 7 4]]

#Get the first row of the above matrix
print(a2[0])
print('='*30)
#Get the middle two lines
print(a2[1:3])
print('='*30)
#Get lines 1, 3, and 4
print(a2[[0,2,3]])
print('='*30)
#Get the second number in the third line
print(a2[2,1])
print('='*30)
#Get two discontinuous numbers
print(a2[[1,2],[2,3]])
print('='*30)
#Get the number of 2, 3 rows, 4, 5 columns
print(a2[1:3,3:5])
print('='*30)
#Get column related operations:
#Get first column
print(a2[:,0])
#Get columns 3 and 4
print('='*30)
print(a2[:,2:3])

result:

[ 0  6 12 18]
==============================
[[ 1  7 13 19]
 [ 2  8 14 20]]
==============================
[[ 0  6 12 18]
 [ 2  8 14 20]
 [ 3  9 15 21]]
==============================
8
==============================
[13 20]
==============================
[[19]
 [20]]
==============================
[0 1 2 3 4 5]
==============================
[[12]
 [13]
 [14]
 [15]
 [16]
 [17]]

Summary:

• Array name [row, column]. For rows and columns, slice and index operations can be used respectively
• Common operations are as follows:
  ([index, index], [[index 1, index 2], [index 3, index 4]], [: (row slice),: (column slice)], [[x (index), y, Z], [[X1 (index), y1],[x2,y2]...])
  Note: a[[1,2],[2,3]] indicates that the two numbers of the third column in the second row and the fourth column in the third row are discontinuous, and a[1:2,2:3] indicates that all the numbers of the third column in the second row and the fourth column in the third row are continuous

Boolean index:

Boolean operations are also vector operations, such as the following code:

a1 = np.arange(0,24).reshape((4,6))
print(a1<10) #A new array will be returned, and all the values in this array are of bool type

result:

[[ True  True  True  True  True  True]
 [ True  True  True  True False False]
 [False False False False False False]
 [False False False False False False]]

a1 = np.arange(0,24).reshape((4,6))
a2 = a1 < 10
print(a1[a2]) #In this way, the value of the position corresponding to the element that is True in a2 will be extracted in a1

result:

[0 1 2 3 4 5 6 7 8 9]

Summary: Boolean operations can include! =, = =, >, <, > =<= And & (and) and | (or).

a1 = np.arange(0,24).reshape((4,6))
a2 = a1[(a1 < 5) | (a1 > 10)]
print(a2)

Substitution of values:

Using the index, you can also replace some values. Replace the value of the position that meets the condition with another value. For example, the following code:

a1 = np.arange(0,24).reshape((4,6))
a1[3] = 0 #Replace all values in the third row with 0
print(a1)

You can also use conditional indexes to:

a1 = np.arange(0,24).reshape((4,6))
a1[a1 < 5] = 0 #Replace all values less than 5 with 0
print(a1)

You can also use functions to implement:

# where function:
a1 = np.arange(0,24).reshape((4,6))
a2 = np.where(a1 < 10,1,0) #Change all numbers less than 10 in a1 to 1 and the rest to 0
print(a2)

Deep copy and shallow copy

When manipulating arrays, their data is sometimes copied into a new array, sometimes not. This is often confusing for beginners. There are three situations:

Do not copy:

a = np.arange(12)
b = a #This will not be copied
print(b is a) #Returns True, indicating that b and a are the same

View or shallow copy:

In some cases, variables will be copied, but the memory space they point to is the same. This situation is called shallow copy, or view. For example, the following code:

a = np.arange(12)
c = a.view()
print(c is a) #Returns False, indicating that c and a are two different variables
c[0] = 100
print(a[0]) #Print 100, indicating that the change to c will affect the value above a, indicating that the memory space they point to is still the same. This is called shallow copy, or view

Deep copy:

Put a complete copy of the previous data into another memory space, which is two completely different values. The example code is as follows:

a = np.arange(12)
d = a.copy()
print(d is a) #Returns False, indicating that d and a are two different variables
d[0] = 100
print(a[0]) #Print 0, indicating that the memory space pointed to by d and a is completely different.

example:

As mentioned earlier, this is the case with flatten and travel. Travel returns View and flatten returns deep copy.

File operation

To manipulate CSV files:

File save:

Sometimes we have an array that needs to be saved to a file, so we can use NP Savetxt. Related functions are described as follows:

np.savetxt(frame, array, fmt='%.18e', delimiter=None)
* frame : File, string, or generator, which can be.gz or.bz2 Compressed file
* array : An array stored in a file
* fmt : The format in which the file is written, for example:%d %.2f %.18e
* delimiter : Split string, default is any space

The following are examples of use:

a = np.arange(100).reshape(5,20)
np.savetxt("a.csv",a,fmt="%d",delimiter=",")

Read file:

Sometimes our data needs to be read from the file, so NP Loadtext. Related functions are described as follows:

np.loadtxt(frame, dtype=np.float, delimiter=None, unpack=False)
* frame: File, string, or generator, which can be.gz or.bz2 Compressed file.
* dtype: Data type, optional.
* delimiter: Split string, default is any space.
* skiprows: Skip front x that 's ok.
* usecols: Reads the specified column and combines it with tuples.
* unpack: If True，The read array is transposed.

np's unique storage solution:

numpy also has a unique storage solution. The file name is in Ending in npy or npz. The following functions are stored and loaded.

• Storage: NP Save (fname, array) or NP savez(fname,array). The extension of the former function is npy, whose extension is npz, which is compressed.
• Loading: NP load(fname).

CSV file operation:

Read csv file:

import csv

with open('stock.csv','r') as fp:
    reader = csv.reader(fp)
    titles = next(reader)#Skip the first line and next moves down the pointer
    for x in reader:
        print(x)

In this way, when obtaining data in the future, it is necessary to obtain data through the following table. If you want to get the data through the title. Then you can use DictReader. The example code is as follows:

with open( 'stock.csv' ,'r') as fp:
#reader object created using DictReader
#The data of the header row will not be included
#reader is an iterator. After traversing the iterator, a dictionary is returned.
reader = csv.DictReader(fp)
for x in reader:
	value = { "name" :x [ 'secShortName ' ], ' volumn ' :x [ ' turnoverVol']}
	print(value)

Write data to csv file:

To write data to a csv file, you need to create a writer object, which mainly uses two methods. One is writerow, and the other is to write a row. One is writerows, and the other is to write multiple rows. The example code is as follows:

import csv

headers = ['name','age','classroom']
values = [
    ('zhiliao',18,'111'),
    ('wena',20,'222'),
    ('bbc',21,'111')
]
with open('test.csv','w',newline='') as fp:
    writer = csv.writer(fp)
    writer.writerow(headers)
    writer.writerows(values)

You can also write data in the form of a dictionary. At this time, you need to use DictWriter. The example code is as follows:

import csv

headers = ['name','age','classroom']
values = [
    {"name":'wenn',"age":20,"classroom":'222'},
    {"name":'abc',"age":30,"classroom":'333'}
]
with open('test.csv','w',newline='') as fp:
    writer = csv.DictWriter(fp,headers)
    writer.writerow({'name':'zhiliao',"age":18,"classroom":'111'})
    writer.writerows(values)

Note: when the header needs to be written:

writer =csv. DictWriter(fp, headers)
#When writing header data, you need to call the writeheader method
writer.witeheader ()

NAN and INF value processing

First of all, we need to know what these two English words mean:

• NAN: Not A number does not mean a number, but it belongs to floating-point type, so you need to pay attention to its type when you want to perform data operations.
• INF: Infinity, which means Infinity, also belongs to floating point type. np.inf means positive Infinity, - NP INF means negative Infinity, which is generally Infinity when the divisor is 0. For example, 2 / 0.

Some features of NAN:

• Nan and Nan are not equal. Like NP NAN != np. The Nan condition is true.
• NAN and any value, the result is NAN.

Sometimes, especially when reading data from files, some missing values often appear. The occurrence of missing values will affect the processing of data. Therefore, we must deal with the missing values before data analysis. There are many ways to deal with it, which need to be done according to the actual situation. There are generally two processing methods: delete the missing value and fill it with other values.

Delete missing values:

Sometimes, if we want to delete the NAN in the array, we can change the idea to extract only the values that are not NAN. The example code is as follows:

# 1. Delete all NAN values. Because the array will not know how to change after deleting the values, it will be turned into a one-dimensional array
data = np.random.randint(0,10,size=(3,5)).astype(np.float)
data[0,1] = np.nan
data = data[~np.isnan(data)] # At this time, the data will have no nan and become a 1-dimensional array

# 2. Delete the line of NAN
data = np.random.randint(0,10,size=(3,5)).astype(np.float)
# Set the (0,1) and (1,2) values to NAN
data[[0,1],[1,2]] = np.NAN
# Get which rows have NAN
lines = np.where(np.isnan(data))[0]
# Use the delete method to delete the specified row. axis=0 indicates the deleted row, and lines indicates the deleted row number
data1 = np.delete(data,lines,axis=0)

be careful:
Except that deiete uses axis=0 to represent rows, most other functions use axis=1 to represent rows.

Replace with other values:

mathematics	English
59	89
90	32
78	45
34	NAN
NAN	56
23	56

If you want to require the total score of each grade and the average score of each grade, you can use some values instead. For example, if you want to calculate the total score, you can replace NAN with 0. If you want to require an average score, you can replace NAN with the average of other values. The example code is as follows:

scores = np.loadtxt("nan_scores.csv",skiprows=1,delimiter=",",encoding="utf-8",dtype=np.str)
scores[scores == ""] = np.NAN
scores = scores.astype(np.float)
# 1. Find out the total score of students' grades
scores1 = scores.copy()
socres1.sum(axis=1)

# 2. Calculate the average score of each course
scores2 = scores.copy()
for x in range(scores2.shape[1]):
    score = scores2[:,x]
    non_nan_score = score[score == score]
    score[score != score] = non_nan_score.mean()
print(scores2.mean(axis=0))

np.random module

np.random provides us with many functions to obtain random numbers. Let's study it here.

np.random.seed:

It is used to specify the integer value at the beginning of the algorithm used to generate random numbers. If the same seed() value is used, the random numbers generated each time are the same. If this value is not set, the system selects this value according to time. At this time, the random numbers generated each time are different due to time differences. Generally, there are no special requirements and no setting is required. The following codes:

np.random.seed(1)
print(np.random.rand()) # Print 0.417022004702574
print(np.random.rand()) # Print other values, because the random number seed will only affect the generation of the next random number.

np.random.rand:

Generate an array with values between [0,1]. The shape is specified by the parameter. If there is no parameter, a random value will be returned. The example code is as follows:

data1 = np.random.rand(2,3,4) # Generate an array of 2 blocks, 3 rows and 4 columns with values from 0 to 1
data2 = np.random.rand() #Generate a random number between 0 and 1

np.random.randn:

Generate mean( μ) 0, standard deviation( σ) The value of the standard normal distribution of 1. The example code is as follows:

data = np.random.randn(2,3) #Generate an array of 2 rows and 3 columns. The values in the array meet the standard positive distribution

np.random.randint:

Generate a random number within the specified range, and you can specify the dimension through the size parameter. The example code is as follows:

data1 = np.random.randint(10,size=(3,5)) #Generate an array with values between 0-10, 3 rows and 5 columns
data2 = np.random.randint(1,20,size=(3,6)) #Generate an array with values between 1-20, 3 rows and 6 columns

np.random.choice:

Randomly sample from a list or array. Or sample from the specified interval. The number of samples can be specified through parameters:

data = [4,65,6,3,5,73,23,5,6]
result1 = np.random.choice(data,size=(2,3)) #Randomly sample from data to generate an array of 2 rows and 3 columns
result2 = np.random.choice(data,3) #Randomly sample three data from data to form a one-dimensional array
result3 = np.random.choice(10,3) #Take 3 values randomly from 0-10

np.random.shuffle:

Scramble the position of the elements of the original array. The example code is as follows:

a = np.arange(10)
np.random.shuffle(a) #The positions of the elements of a will be changed randomly

more:

For more random module documentation, please refer to Numpy's official documentation: https://docs.scipy.org/doc/numpy/reference/routines.random.html

Axis understanding

In short, the outermost parentheses represent axis=0, and the counting of axis corresponding to the inward parentheses is increased by 1 in turn. What do you mean? Let's explain it again.

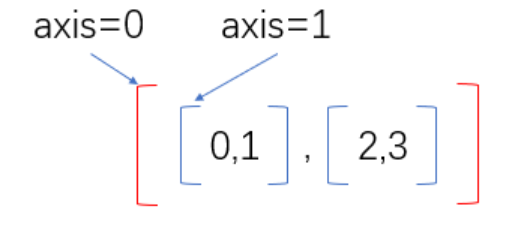
The outer bracket is axis=0, and the inner two sub brackets are axis=1. Operation mode: if the axis is specified for relevant operations, it will use the position 0, position 1, position 2... Of each direct child element under the axis for relevant operations respectively.
Now let's do a few operations in the way we just understood. For example, there is a two-dimensional array:

x = np.array([[0,1],[2,3]])

1. Find the sum of x array in the case of axis=0 and axis=1:

>>> x.sum(axis=0)
 array([2, 4])

The reason why we get [2,4] is that if we add it in the way of axis=0, we will add the 0th position and the first position of all direct child elements under the outermost axis... And so on, we get 0 + 2 and 2 + 3, and then add them to get [2,4].

 >>> x.sum(axis=1)
 array([1, 5])

Because we add in the way of axis=1, the elements with axis 1 will be taken out for summation. The result is 0,1, which is added as 1, and 2,3 is added as 5. Therefore, the final result is [1,5].

1. Use NP Max finds the maximum value when axis=0 and axis=1:

import  numpy as np
np.random.seed(100)
x = np.random.randint(0,10,size=(3,5))
print(x)
x.max(axis=0)

result:

[[8 8 3 7 7]
 [0 4 2 5 2]
 [2 2 1 0 8]]
array([8, 8, 3, 7, 8])

Because we calculate the maximum value according to axis=0, we will find the direct child element in the outermost axis, then put the 0th value of each child element together for the maximum value, put the first value together for the maximum value, and so on. If axis=1, you can get each direct child element and find the maximum value of each child element:

x.max(axis=1)

result:

array([8, 5, 8])

1. Use NP Delete deletes elements when axis=0 and axis=1:

x = np.array([[0,1],[2,3]])

 >>> np.delete(x,0,axis=0)#
 array([[2, 3]])

np.delete is an exception. If we delete it in the way of axis=0, it will first find the 0 in the direct child element under the outermost bracket, and then delete it, leaving the data in the last row.

>>> np.delete(x,0,axis=1)
 array([[1],
        [3]])

Similarly, if we delete according to axis=1, the data in the first column will be deleted.

For the delete function:
The delete function in numpy has three parameters:
numpy.delete(arr, obj, axis)
arr: matrix to be processed
obj: where is it processed
Axis: This is an optional parameter, axis = None, 1, 0

axis=None: arr will expand by row first, then delete the number at position obj-1 (starting from 0) by obj, and return a row matrix.

axis = 0: arr delete by line

axis = 1: arr delete by column

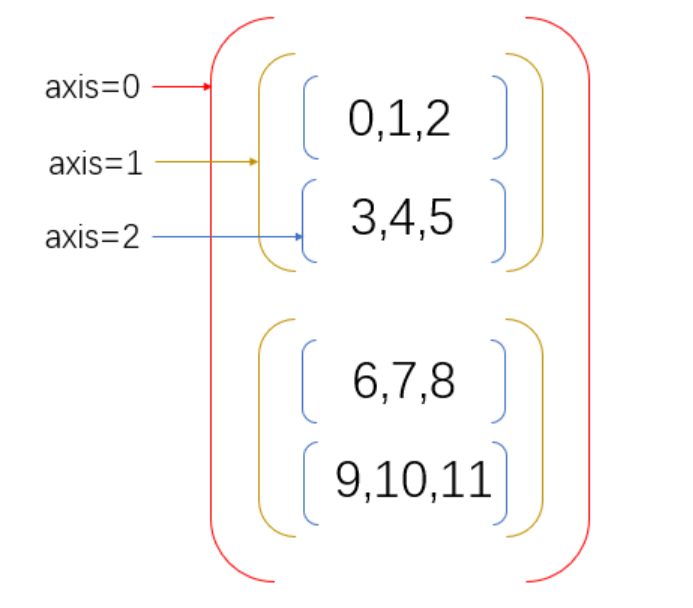
Three dimensional array:

General function

Unary function:

function	describe
np.abs	absolute value
np.sqrt	Root opening
np.square	square
np.exp	Calculate index (e^x)
np.log，np.log10，np.log2，np.log1p	Find the logarithm with e as the base, 10 as the low, 2 as the low and (1+x) as the base
np.sign	Label the values in the array. Those greater than 0 become 1, those equal to 0 become 0, and those less than 0 become - 1
np.ceil	Rounding in the direction of infinity, for example, 5.1 becomes 6 and - 6.3 becomes - 6
np.floor	Forensics in the direction of negative infinity. For example, 5.1 will become 5 and - 6.3 will become - 7
np.rint，np.round	Returns the rounded value
np.modf	Separate integers and decimals to form two arrays
np.isnan	Determine whether it is nan
np.isinf	Determine if it is inf
np.cos，np.cosh，np.sin，np.sinh，np.tan，np.tanh	trigonometric function
np.arccos，np.arcsin，np.arctan	Inverse trigonometric function

Binary function:

function	describe
np.add	Addition operation (i.e. 1 + 1 = 2), equivalent to+
np.subtract	Subtraction (i.e. 3-2 = 1), equivalent to-
np.negative	Negative number operation (i.e. - 2) is equivalent to adding a minus sign
np.multiply	Multiplication (i.e. 2 * 3 = 6), equivalent to*
np.divide	Division operation (i.e. 3 / 2 = 1.5), equivalent to/
np.floor_divide	Rounding operation, equivalent to//
np.mod	Remainder operation, equivalent to%
greater,greater_equal,less,less_equal,equal,not_equal	>,>=,<,<=,=,!= Function expression for
logical_and	&Function expression for
logical_or	|Function expression for

Aggregate function:

The Security version, that is, the element value is NAN, does not affect the corresponding calculation

Function name	NAN Security version	describe
np.sum	np.nansum	Calculate the sum of elements
np.prod	np.nanprod	Calculate the product of elements
np.mean	np.nanmean	Calculate the average of the elements
np.std	np.nanstd	Calculate the standard deviation of the element
np.var	np.nanvar	Calculate the variance of the element
np.min	np.nanmin	Calculate the minimum value of the element
np.max	np.nanmax	Calculate the maximum value of the element
np.argmin	np.nanargmin	Find the index of the minimum value
np.argmax	np.nanargmax	Find the index of the maximum value
np.median	np.nanmedian	Calculate the median of the element

Use NP Sum or a.sum can be implemented. And when using, you can specify which axis. Similarly, python also has a built-in sum function, but the execution efficiency of Python's built-in sum function is not NP Sum is so high that you can learn from the following code tests:

a = np.random.rand(1000000)
%timeit sum(a) #Use Python's built-in sum function to find the sum and see the time spent
%timeit np.sum(a) #Use Numpy's sum function to sum and look at the time it takes

result:

73.3 ms ± 1.47 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
899 µs ± 39.5 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

Explanation:

• Timing of single line code execution:% timeit
• Timing of multiline code execution:%% timeit:

It can only be used under ipython. (so, of course, Jupiter notebook can be used, and the python environment in pycham is also Jupiter notebook.)
%timeit can measure how long a line of code executes multiple times
%%timeit can measure the execution time of multiple lines of code

Boolean array functions:

Function name	describe
np.any	Verify that any element is true
np.all	Verify that all elements are true

For example, to see if all elements in the array are 0, you can use the following code:

np.all(a==0) 
# Or
(a==0).all()

For example, if we want to see whether there is a number equal to 0 in the array, we can implement it through the following code:

np.any(a==0)
# Or
(a==0).any()

Sort:

1. np.sort: Specifies the axis to sort. The default is to sort using the last axis of the array.

a = np.random.randint(0,10,size=(3,5))
b = np.sort(a) #Sort by row. Because the last axis is 1, the innermost elements are sorted.
c = np.sort(a,axis=0) #Sort by column because axis=0 is specified
print(a)
print('='*30)
print(b)
print('='*30)
print(c)

result:

[[1 6 5 9 2]
 [1 6 8 7 2]
 [8 5 5 3 8]]
==============================
[[1 2 5 6 9]
 [1 2 6 7 8]
 [3 5 5 8 8]]
==============================
[[1 5 5 3 2]
 [1 6 5 7 2]
 [8 6 8 9 8]]

And darray Sort(), this method will directly affect the original array, rather than returning a new sorted array.

1. np.argsort: returns the sorted subscript value. The example code is as follows:

np.argsort(a) #By default, the last axis is also used for sorting.

result:

array([[0, 4, 2, 1, 3],#This subscript is the value of the original array a, that is, the first element in the first row of the original array A is ranked first, and the fifth element is ranked second
       [0, 4, 1, 3, 2],
       [3, 1, 2, 0, 4]], dtype=int64)

1. Descending sort: NP Sort will sort in ascending order by default. If we want to sort in descending order. Then the following scheme can be adopted:

 # 1. Use a minus sign
 -np.sort(-a)

 # 2. Use sort, argsort and take
 indexes = np.argsort(-a) #The sorted results are in descending order
 np.take(a,indexes) #Extract the corresponding elements from a according to the subscript

Other functions supplement:

1. np.apply_along_axis: executes the specified function along an axis. The example code is as follows:

 # Find the average value of array a according to rows, and remove the maximum and minimum values.
 np.apply_along_axis(lambda x:x[(x != x.max()) & (x != x.min())].mean(),axis=1,arr=a)#Each row of the array is passed to x

1. np.linspace: used to divide the values in a specified interval into equal parts. The example code is as follows:

 # Divide 0-1 into 12 points to generate an array
 np.linspace(0,1,12)

1. np.unique: returns the unique value in the array.

 # Returns the unique value in array a, and returns the number of occurrences of each unique value.
 np.unique(a,return_counts=True)

more:

https://docs.scipy.org/doc/numpy/reference/index.html