Anyway, brother y said that he would definitely enter the national competition after brushing. I'll try~

1, Recursion and recursion

92. Recursive implementation of exponential enumeration (simple)

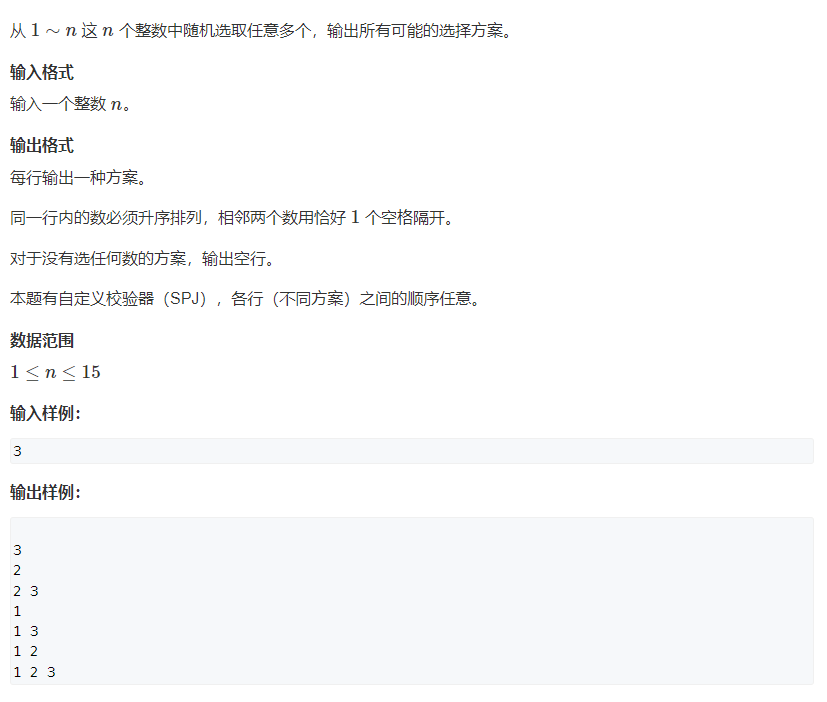
Note that this problem is to solve the combination!!

import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	static LinkedList<Integer> tmp = new LinkedList<>();
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		dfs(n, 1);
	}
	static void dfs(int n, int start) {
		if (tmp.size() == 0) System.out.println();
		if (tmp.size() > 0) {
			for (int i = 0; i < tmp.size(); i++) {
				System.out.printf("%d ", tmp.get(i));
			}
			System.out.println();
		}
		if (tmp.size() > n) return;
		for (int i = start; i <= n; i++) {
			tmp.add(i);
			dfs(n, i + 1);
			// to flash back
			tmp.removeLast();
		}
	}
}

94. Recursive implementation of permutation enumeration (simple)

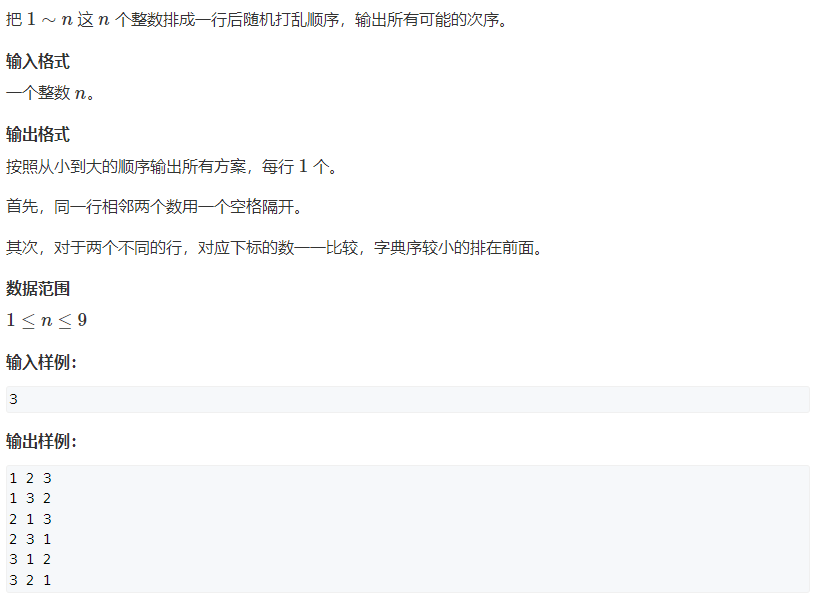
Pay attention to the arrangement, and use the vis array. When outputting the results, pay attention to using BufferedWriter to save time.

import java.io.BufferedWriter;
import java.io.IOException;
import java.io.OutputStreamWriter;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	static BufferedWriter log = new BufferedWriter(new OutputStreamWriter(System.out));
	static LinkedList<Integer> tmp = new LinkedList<>();
	static boolean[] vis;
	public static void main(String[] args) throws IOException {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		vis = new boolean[n + 1];
		dfs(n);
		// When the BufferedWriter is used up, be sure to flush, otherwise it will not be output
		log.flush();
	}
	static void dfs(int n) throws IOException {
		if (tmp.size() == n) {
			for (int i = 0; i < tmp.size(); i++) {
				log.write(tmp.get(i) + " ");
			}
			log.write("\n");
		}
		if (tmp.size() > n) return;
		for (int i = 1; i <= n; i++) {
			if (vis[i]) continue;
			tmp.add(i);
			vis[i] = true;
			dfs(n);
			// to flash back
			vis[i] = false;
			tmp.removeLast();
		}
	}
}

717. Simple Fibonacci (medium)

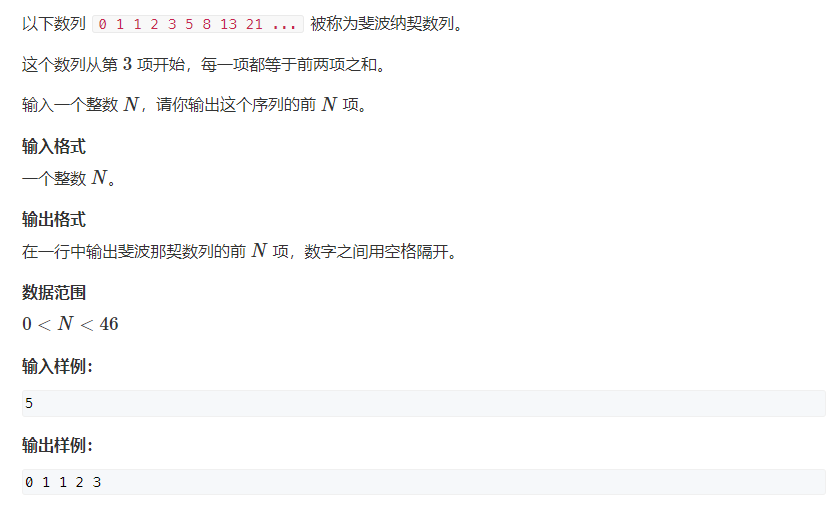
import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int[] f = new int[47];
		f[0] = 0;
		f[1] = 1;
		f[2] = 1;
		for (int i = 3; i < n; i++) {
		    f[i] = f[i - 1] + f[i - 2];
		}
		for (int i = 0; i < n; i++) {
			System.out.printf("%d ", f[i]);
		}
	}
}

95. Puzzling switch (medium) (state compression enumeration)

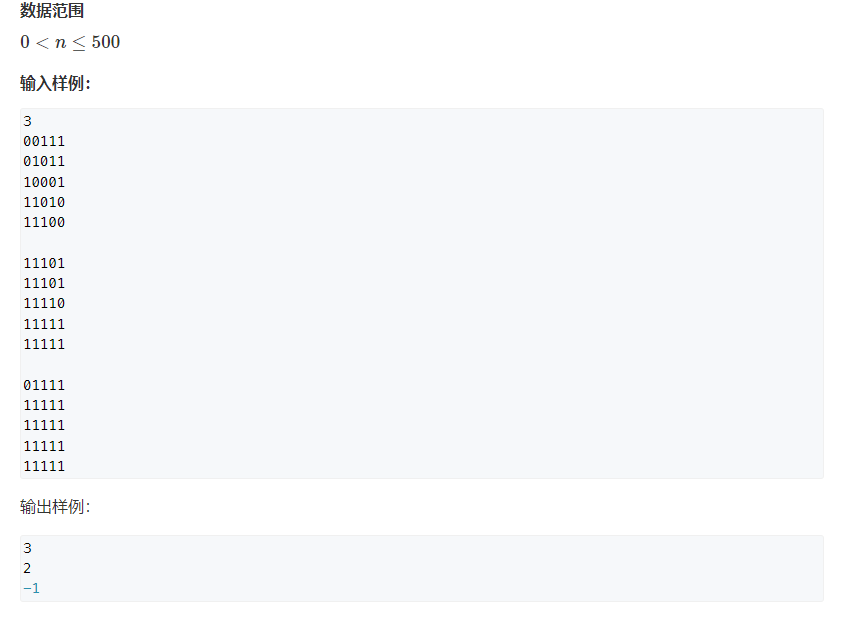
Let's start with the conclusion: after the state of the first line is determined, the state of the second line is also determined (that is, press a button directly below the first line 0), and so on. The third and fourth lines are also determined. We only need to judge whether the last line is all 1, so we can determine whether they are all lit, because the front affirmation is lit.

To enumerate the states of the first line, you can use binary string to enumerate through state compression. There are five switches in a line, and each switch has two states. There are 2 ^ 5 = 32 states in total. 00000 represents not pressing all and 11111 represents pressing all (note that 0 and 1 here are different from those in the title. 0 and 1 here are used to enumerate multiple states of the first line)

Also pay attention to the copy of the array!!!

import java.util.Arrays;
import java.util.Scanner;

public class Main {
	// 5 directions including self point
	static int[] x = new int[] {1,-1,0,0,0};
	static int[] y = new int[] {0,0,1,-1,0};
	static char[][] map;
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		map = new char[5][5];
		while ((n--) > 0) {
			for (int i = 0; i < 5; i++) {
				map[i] = scan.next().toCharArray();
			}
			// Backup map
			char[][] backUp = new char[5][5];
			for (int i = 0; i < 5; i++) {
				backUp[i] = Arrays.copyOf(map[i], 5);
			}
			// Global results
			int ans = 7;
			// All operations that traverse the first row may be 2 ^ 5
			for (int i = 0; i < (1 << 5); i++) {
				// Traverse the minimum operand in the current first line state
				int count = 0;
				// 5 digits. Press the position switch to see which digit is 1
				for (int j = 0; j < 5; j++) {
					if (((i >> j) & 1) == 1) {
						// Press the button on line 1
						turn(0, j);
						count++;
					}
				}
				// Start traversing the following lines, and the last line is used for judgment
				for (int j = 0; j < 4; j++) {
					for (int k = 0; k < 5; k++) {
						if (map[j][k] == '0') {
							// The light in the first row is not on. The status of the first row has been determined
							// The light directly below must be pressed
							turn(j + 1, k);
							count++;
						}
					}
				}
				// check whether the last line is all 1
				boolean flag = false;
				for (int j = 0; j < 5; j++) {
					if (map[4][j] == '0') {
						flag = true;
						break;
					}
				}
				// Update global answers
				if (flag == false) {
					ans = Math.min(ans, count);
				}
				// Restore map
				// Be sure to restore and save the map by copy. Don't directly = variable name
				for (int j = 0; j < 5; j++) {
					map[j] = Arrays.copyOf(backUp[j], 5);
				}
			}
			if (ans > 6) System.out.println(-1);
			else System.out.println(ans);
		}
	}
	// push switch 
	static void turn(int i, int j) {
		for (int k = 0; k < 5; k++) {
			int tx = i + x[k];
			int ty = j + y[k];
			if (tx < 0 || ty < 0 || tx >= 5 || ty >= 5) continue;
			// XOR
			map[tx][ty] ^= 1;
		}
	}
}

Don't take the above problem for granted. It's not so complex. It's state compression, and you only need to traverse the state of the first line.

93. Recursive implementation of combinatorial enumeration (simple)

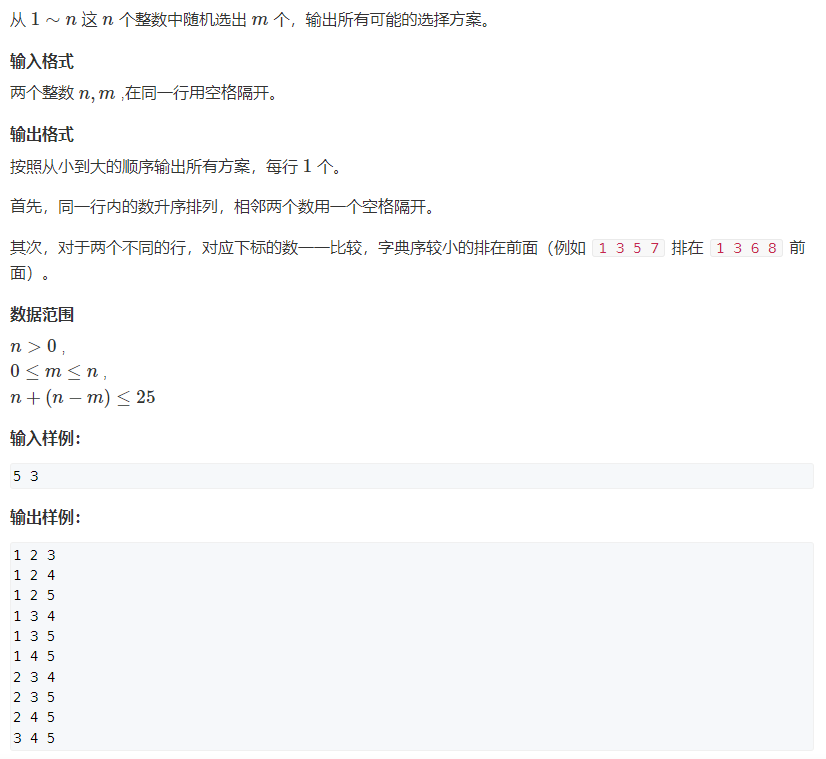
For normal dfs, no vis record is needed. Just pay attention to the length of the array.

import java.io.BufferedWriter;
import java.io.IOException;
import java.io.OutputStreamWriter;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	static BufferedWriter log = new BufferedWriter(new OutputStreamWriter(System.out));
	static LinkedList<Integer> ans = new LinkedList<>();
	public static void main(String[] args) throws IOException {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int m = scan.nextInt();
		dfs(n, m, 1);
		// BufferdWriter must flush
		log.flush();
	}
	static void dfs(int n, int m, int start) throws IOException {
		if (ans.size() == m) {
			for (int num : ans) {
				log.write(num + " ");
			}
			log.write("\n");
			return;
		}
		if (ans.size() > m) return;
		for (int i = start; i <= n; i++) {
			ans.add(i);
			dfs(n, m, i + 1);
			// to flash back
			ans.removeLast();
		}
	}
}

1209. With score (simple) (DFS search + violence enumeration)

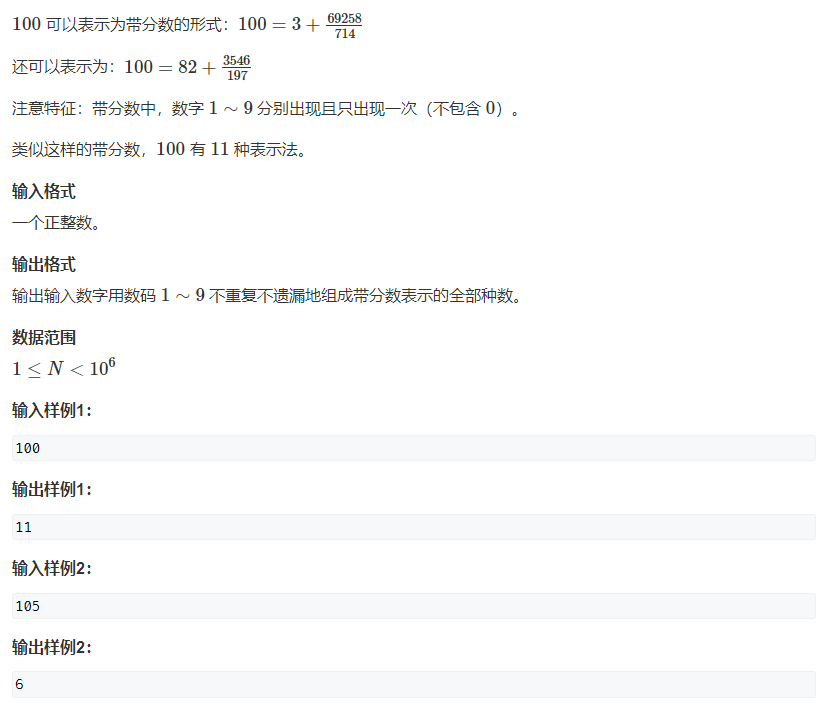
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	static LinkedList<Integer> tmp = new LinkedList<>();
	static boolean[] vis = new boolean[10];
	static int n;
	static int ans = 0;
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		n = scan.nextInt();
		dfs();
		System.out.println(ans);
	}
	static void dfs() {
		if (tmp.size() > 9) return;
		// Arrangement of 9 numbers
		if (tmp.size() == 9) {
			// n = a + b/c, a can only have 1 or 2 digits
			// n * c = a * c + b
			// Traversal enumeration of three numbers
			int a = 0;
			for (int i = 0; i < 9 - 2; i++) {
				a = a * 10 + tmp.get(i);
				if (a >= n) continue;
				int b = 0;
				for (int j = i + 1; j < 9 - 1; j++) {
					b = b * 10 + tmp.get(j);
					int c = 0;
					for (int k = j + 1; k < 9; k++) {
						c = c * 10 + tmp.get(k);
						// Meet the question conditions and use up all the numbers
						if (n * c == a * c + b && k == 8) {
							ans++;
							break;
						}
					}
				}
			}
			return;
		}
		for (int i = 1; i <= 9; i++) {
			if (vis[i]) continue;
			vis[i] = true;
			tmp.add(i);
			dfs();
			vis[i] = false;
			tmp.removeLast();
		}
	}
}

It took seconds to brush this question before. Now I have met it or thought about it for a while... I'm really good at different topics at each stage... (brain capacity is really limited)

116. Pilot brothers (simple) (DFS search)

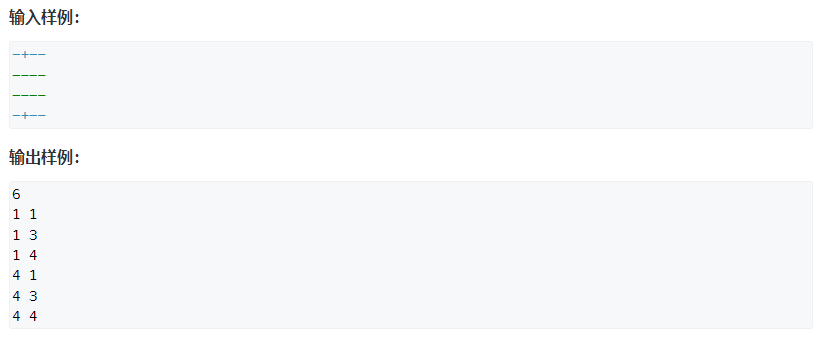
Note that this problem cannot be done with state compression + enumeration, because pressing the switch will affect a whole row and a whole column, no longer up, down, left and right!!

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;

class node {
	int x, y;
	node(){};
	node(int x, int y) {
		this.x = x;
		this.y = y;
	}
}
public class Main {
	static char[][] map;
	static boolean[][] vis;
	static LinkedList<node> ansNodes = new LinkedList<>();
	static int ans = Integer.MAX_VALUE;
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		map = new char[4][4];
		vis = new boolean[4][4];
		for (int i = 0; i < 4; i++) {
			map[i] = scan.next().toCharArray();
		}
		dfs(0, 0, 0, new LinkedList<>());
		System.out.println(ans);
		for (node t : ansNodes) {
			System.out.println(t.x + " " + t.y);
		}
	}
	static void dfs(int x, int y, int cnt, LinkedList<node> tmp) {
		if (y == 4) {
			x++;
			y = 0;
		}
		if (x == 4) {
			boolean flag = true;
			for (int i = 0; i < 4; i++) {
				for (int j = 0; j < 4; j++) {
					if (map[i][j] == '+') {
						flag = false;
						break;
					}
				}
				if (flag == false) break;
			}
			if (flag) {
				if (cnt < ans) {
					ans = cnt;
					ansNodes = new LinkedList<>(tmp);
				}
			}
			return;
		}
		if (vis[x][y]) return;
		// Press the current switch and its row and column switches
		turn(x, y);
		vis[x][y] = true;
		// Record coordinates
		tmp.add(new node(x + 1, y + 1));
		dfs(x, y + 1, cnt + 1, new LinkedList<>(tmp));
		// to flash back
		turn(x, y);
		vis[x][y] = false;
		tmp.removeLast();
		dfs(x, y + 1, cnt, new LinkedList<>(tmp));
	}
	static void turn(int x, int y) {
		for (int i = 0; i < 4; i++) {
			if (map[x][i] == '+') map[x][i] = '-';
			else map[x][i] = '+';
			if (map[i][y] == '+') map[i][y] = '-';
			else map[i][y] = '+';
		}
		if (map[x][y] == '+') map[x][y] = '-';
		else map[x][y] = '+';
	}
}

1208. Coin flipping (simple) (greedy)

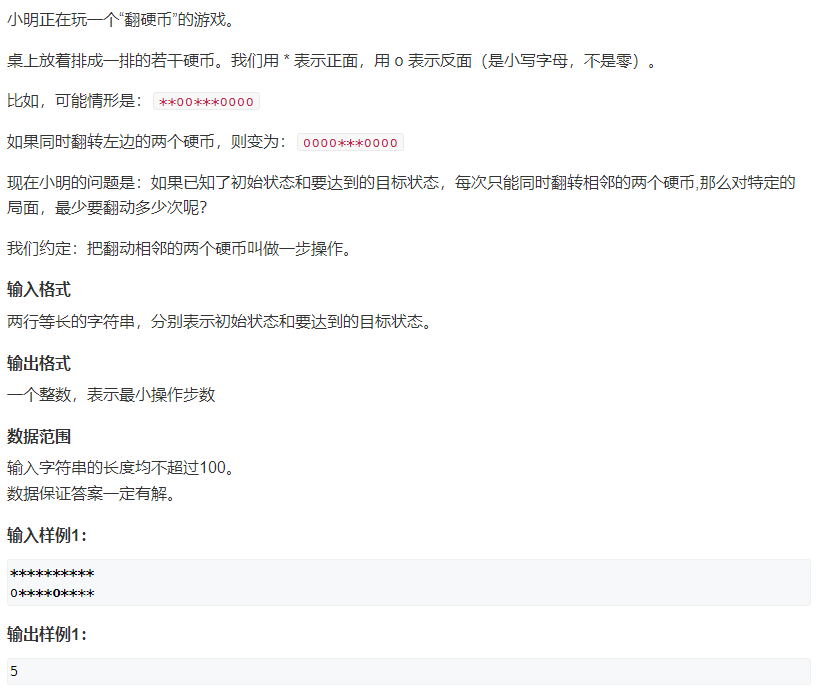
At the beginning, I thought about DFS and state compression, and found that it was OK to be greedy directly.

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		String origin = scan.next();
		String dest = scan.next();
		char[] org = origin.toCharArray();
		char[] des = dest.toCharArray();
		// Greedy, compare each coin, and flip it if it's different
		int count = 0;
		for (int i = 0; i < org.length - 1; i++) {
			if (org[i] == des[i]) continue;
			count++;
			org[i] = org[i] == '*' ? 'o' : '*';
			org[i + 1] = org[i + 1] == '*' ? 'o' : '*';
		}
		System.out.println(count);
	}
}

2, Dichotomy and prefix sum

789. Number range (simple) (ordinary bisection template)

It's a good topic to review the binary template. Well ~, I made a mistake in detail.

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	static int[] nums;
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int q = scan.nextInt();
		nums = new int[n];
		for (int i = 0; i < n; i++) {
			nums[i] = scan.nextInt();
		}
		while ((q--) > 0) {
			int key = scan.nextInt();
			// Find the starting position first
			int a = binarySearch1(key);
			if (a == -1) {
				// Not at first, not at last
				System.out.printf("-1 -1\n");
			} else {
				int b = binarySearch2(key);
				System.out.printf("%d %d\n", a, b - 1);
			}
		}
	}
	// Record the location of the first occurrence
	public static int binarySearch1(int key) {
		int left = 0;
		int right = nums.length - 1;
		int ans = -1;
		int mid;
		while (left <= right) {
			mid = left + (right - left) / 2;
			if (nums[mid] == key) {
				ans = mid;
				// Continue to look to the left for the first subscript that appears
				right = mid - 1;
			} else if (nums[mid] < key) {
				left = mid + 1;
			} else {
				right = mid - 1;
			}
		}
		return ans;
	}
	// Record the last position (find the last position greater than the key)
	public static int binarySearch2(int key) {
		int left = 0;
		int right = nums.length;
		int mid;
		while (left < right) {
			mid = left + (right - left) / 2;
			if (nums[mid] > key) {
				right = mid;
			} else {
				left = mid + 1;
			}
		}
		// If not found, the length of the array is returned
		return left;
	}
}

790, the third power of the number (simple) (floating point binary template)

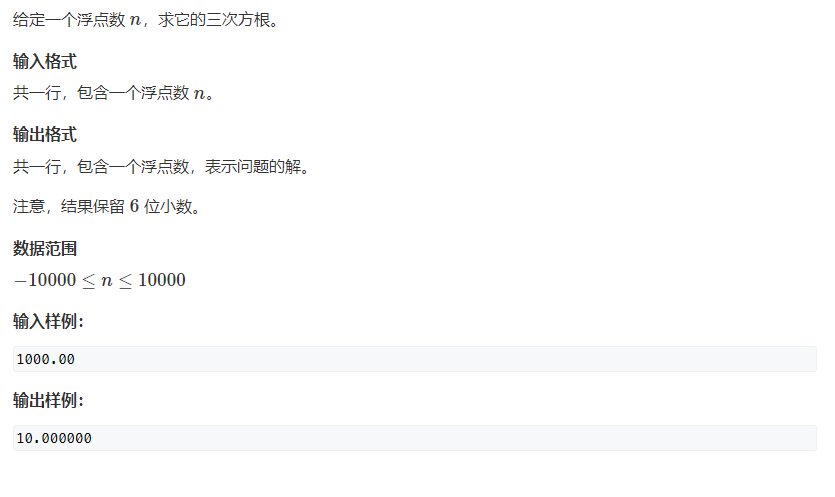
For the binary template of floating-point number, left is the data range given by the topic, and right is also the data range given by the topic. The judgment condition of while becomes the precision eps of right - left. Each update directly left = mid, or right = mid.

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		double n = scan.nextDouble();
		double eps = 0.0000001;
		double left = -10000;
		double right = 10000;
		double mid;
		while (right - left > eps) {
			mid = left + (right - left) / 2;
			if (mid * mid * mid <= n) {
				left = mid;
			} else {
				right = mid;
			}
		}
		System.out.printf("%.6f", left);
	}
}

795, prefix and (simple) (one-dimensional prefix and)

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int m = scan.nextInt();
		int[] nums = new int[n];
		// Prefix and array
		int[] preSum = new int[n + 1];
		for (int i = 0; i < n; i++) {
			nums[i] = scan.nextInt();
			preSum[i + 1] = nums[i] + preSum[i];
		}
		while ((m--) > 0) {
			int l = scan.nextInt();
			int r = scan.nextInt();
			System.out.println(preSum[r] - preSum[l - 1]);
		}
	}
}

796. Sum of submatrix (simple) (two-dimensional prefix sum)

The one-dimensional prefix is easy to understand, but the two-dimensional prefix is not easy to understand. Definition: take (1, 1) as the upper left corner and (i, j) as the sum of the numbers in the lower right corner of the matrix.

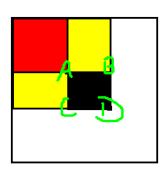
Suppose we know the sum of each matrix. Taking the figure above as an example, we want to ask the sum of the black part, the coordinates of D are (i, j) and the side length of ABCD is 1. How to convert?

=f[i][j] - f[i - 1][j] - f[i][j - 1] + f[i - 1]f[j - 1]

Isn't it very simple? If you understand the two-dimensional prefix and, you'd better remember the picture above.

How to find the prefix and sum of each matrix?

Similarly, using the above figure, let's assume that the black block of ABCD represents a number. Now it is required f[i][j]:
=Numeric value of f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + ABCD

OK ~ let's do the problem~

Enter an integer matrix with n rows and m columns, and then enter q queries. Each query contains four integers x1, Y1, X2 and Y2, representing the upper left corner coordinates and lower right corner coordinates of a sub matrix.

For each query, the sum of all numbers in the output submatrix.

Input format
The first line contains three integers n, m, q.

The next n rows contain m integers, representing the integer matrix.

The next q line contains four integers x1, Y1, X2 and Y2, representing a set of queries.

Output format
There are q rows in total, and each row outputs a query result.

Data range
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
− 1000 ≤ value of elements in the matrix ≤ 1000
Input sample:
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
Output example:
17
27
21

It should be noted whether the title contains the coordinate points in the upper left corner and the lower right corner. If so, it will be slightly adjusted. See the code for details:

import java.util.Arrays;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int m = scan.nextInt();
		int q = scan.nextInt();
		int[][] map = new int[n + 1][m + 1];
		// Prefix and array
		int[][] preSum = new int[n + 1][m + 1];
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				map[i][j] = scan.nextInt();
				// As with one-dimensional, it can be read and calculated at the same time
				preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + map[i][j];
			}
		}
		while ((q--) > 0) {
			int x1 = scan.nextInt();
			int y1 = scan.nextInt();
			int x2 = scan.nextInt();
			int y2 = scan.nextInt();
			// Don't be afraid to forget the formula. Think back to that picture
			// [x1-1][y2] and [x2][y1-1] are used here because the point of [x1][y1] is included
			System.out.println(preSum[x2][y2] - preSum[x1 - 1][y2] - preSum[x2][y1 - 1] + preSum[x1 - 1][y1 - 1]);
		}
	}
}

730. Robot jumping problem (medium) (binary search answer)

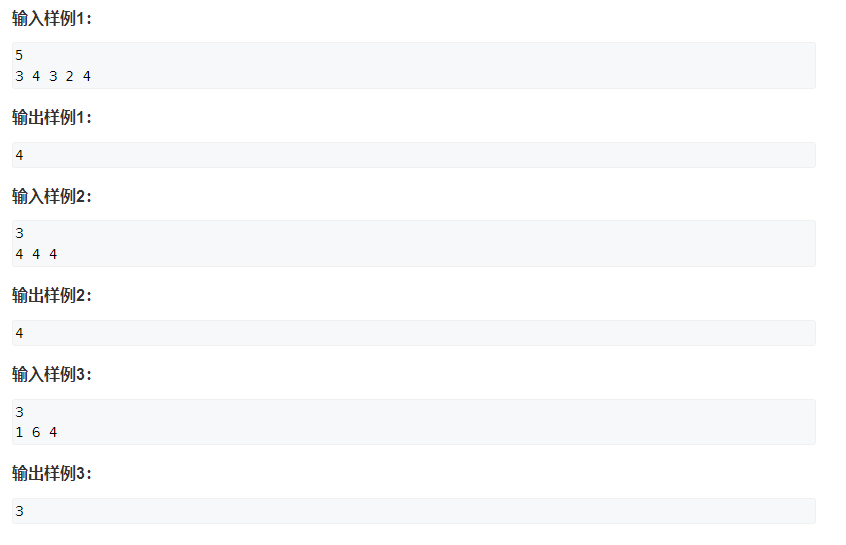
Just a two-point answer.

import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	static int[] nums;
	static int n;
	static int max;
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		n = scan.nextInt();
		nums = new int[n];
		max = Integer.MIN_VALUE;
		for (int i = 0; i < n; i++) {
			nums[i] = scan.nextInt();
			if (nums[i] > max) max = nums[i];
		}
		// Find the answer two points
		int left = 0;
		int right = max;
		int mid;
		int ans = 0;
		while (left <= right) {
			mid = left + (right - left) / 2;
			if (check(mid)) {
				ans = mid;
				right = mid - 1;
			} else {
				left = mid + 1;
			}
		}
		System.out.println(ans);
	}
	// See if the current answer meets the requirements
	public static boolean check(int num) {
		int tmp = num;
		for (int i = 0; i < n; i++) {
			if (nums[i] > tmp) {
				tmp -= (nums[i] - tmp);
			} else {
				tmp += (tmp - nums[i]);
			}
			if (tmp < 0) return false;
			// Once it is greater than the maximum value in the current array, you will add blood wherever you go
			// Here, you must return true in advance, otherwise the accumulation will exceed the range of int and become a negative number, which will affect the judgment
			if (tmp >= max) return true;
		}
		return true;
	}
}

1221. Sum of Squares Theorem (simple) (hash table, sum of n numbers)

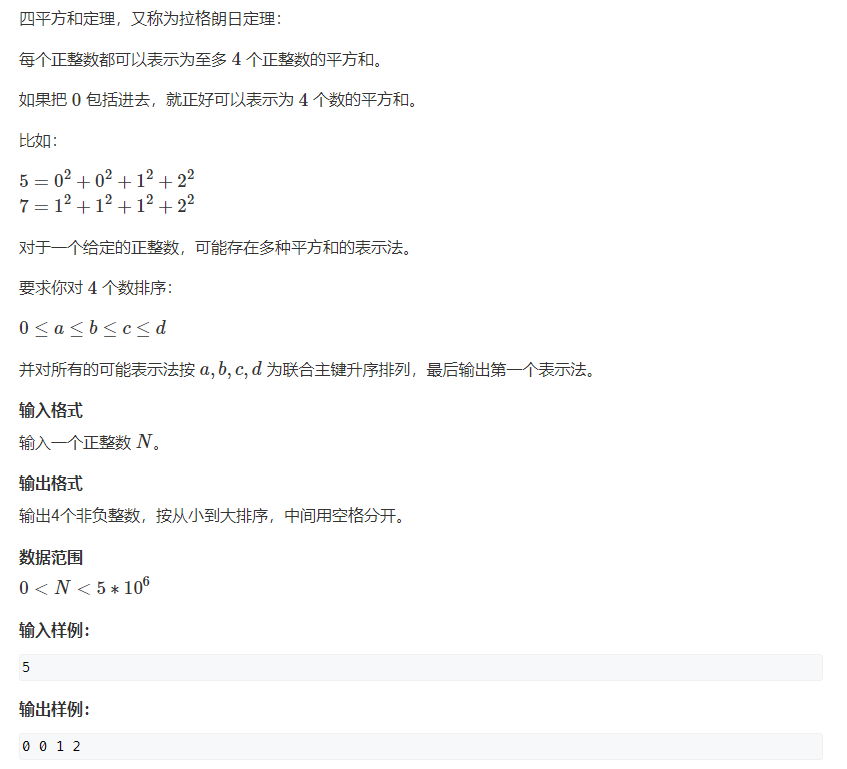
At that time, in the system of playing the Blue Bridge Cup, the triple cycle violence of this problem was over. Acwing strengthened the data violence to timeout. Use the hash table to store the last two numbers first, and then traverse the first two numbers. Pay attention to the dictionary order. Therefore, once there are several numbers in the hash table, it can't be put again. The number put in for the first time is the best.

This solution is common in the sum of n numbers in LeetCode, which is explained in detail in my topic on hash tables.

import java.util.Arrays;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		String[] strings = new String[5000000];
		for (int i = 0; i * i <= n; i++) {
			for (int j = i; i * i + j * j <= n; j++) {
				// Note that if you have found it before, don't look for it, because the best one is found at the beginning
				if (strings[i * i + j * j] == null) {
					strings[i * i + j * j] = i + " " + j;
				}
			}
		}
		boolean flag = false;
		for (int i = 0; i * i <= n; i++) {
			for (int j = i; i * i + j * j <= n; j++) {
				if (strings[n - i * i - j * j] != null) {
					System.out.println(i + " " + j + " " +strings[n - i * i - j * j]);
					flag =  true;
					break;
				}
			}
			if (flag) break;
		}
	}
}

1227. Chocolate (simple) (binary search answer)

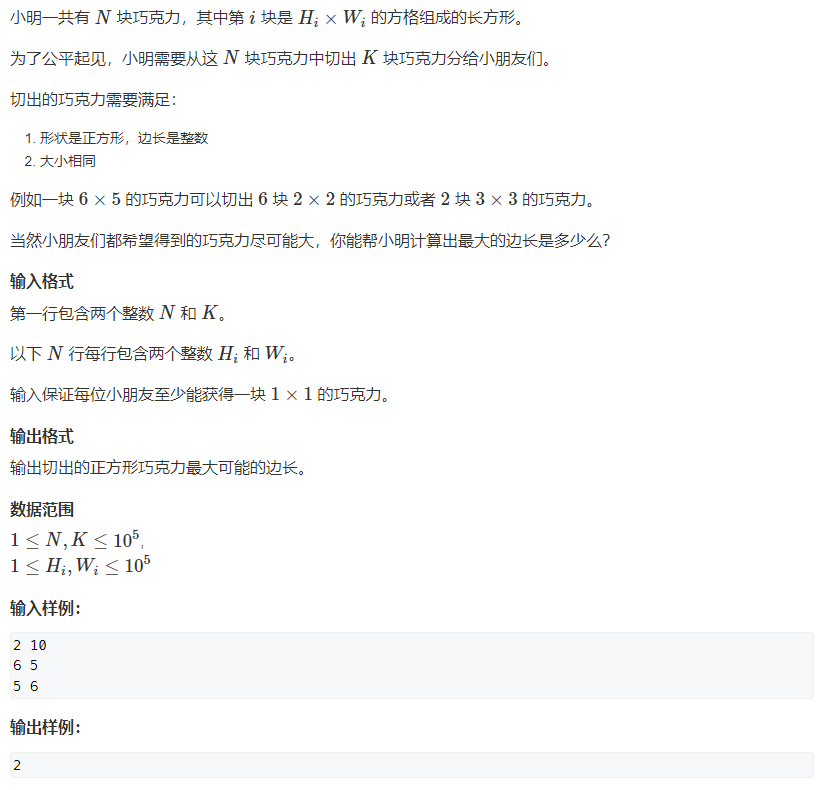
The number of pieces that can be divided out of a piece of chocolate = (length / minute side length) * (width / minute side length), so don't you just follow the same question and find the answer directly by two points~

import java.util.Arrays;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	static int[] h;
	static int[] w;
	static int n, k;
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		n = scan.nextInt();
		k = scan.nextInt();
		h = new int[n];
		w = new int[n];
		int max = Integer.MIN_VALUE;
		for (int i = 0; i < n; i++) {
			h[i] = scan.nextInt();
			max = Math.max(h[i], max);
			w[i] = scan.nextInt();
			max = Math.max(w[i], max);
		}
		// The last edge that meets the requirements is the maximum edge length
		int left = 1;
		int right = max;
		int mid;
		int ans = -1;
		while (left <= right) {
			mid = left + (right - left) / 2;
			if (check(mid)) {
				ans = mid;
				// Try to expand the side length
				left = mid + 1;
			} else {
				right = mid - 1;
			}
		}
		System.out.println(ans);
	}
	public static boolean check(int len) {
		int count = 0;
		for (int i = 0; i < n; i++) {
			count += (h[i] / len) * (w[i] / len);
		}
		return count >= k;
	}
}

99. Laser bomb (simple) (two-dimensional prefix and)

The essence is to find the sum of two-dimensional prefixes, and then turn it into the maximum sum of all squares of R. if it is found that the final ans is still the minimum value, it means that the missile is too large and can be blown up.

import java.util.Arrays;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int r = scan.nextInt();
		int[][] map = new int[5010][5010];
		for (int i = 0; i < n; i++) {
			int a = scan.nextInt();
			int b = scan.nextInt();
			int w = scan.nextInt();
			// To facilitate the calculation of prefix and
			// Note that different targets can be in the same position
			map[a + 1][b + 1] += w;
		}
		// Calculate prefix and
		int[][] preSum = new int[5010][5010];
		for (int i = 1; i <= 5001; i++) {
			for (int j = 1; j <= 5001; j++) {
				preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + map[i][j];
			}
		}
		// The bombing range is square
		// Traverse the lower right coordinate
		int ans = Integer.MIN_VALUE;
		for (int i = r; i <= 5001; i++) {
			for (int j = r; j <= 5001; j++) {
				int tmp = preSum[i][j] - preSum[i - r][j] - preSum[i][j - r] + preSum[i - r][j - r];
				ans = Math.max(ans, tmp);
			}
		}
		// If ans is still the minimum value, the missile is too large!
		if (ans == Integer.MIN_VALUE) System.out.println(preSum[5000][5000]);
		else System.out.println(ans);
	}
}

1230, k-times interval (medium) (prefix and + mathematical conversion)

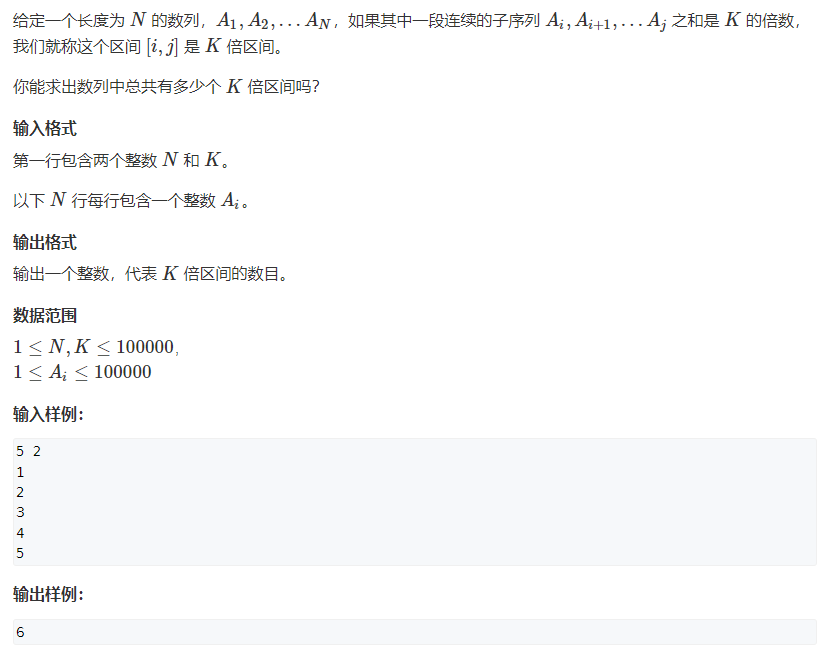
At first glance, it is the prefix and, but it will timeout. Try to optimize.

The questions I brushed before... I forgot again... One brush is not enough!

Considering that the prefix and interval [i, j] = prefix [J + 1] - prefix [i] (where i, j starts from 0) are multiples of K, then prefix [J + 1]% k = prefix [i]% k, so we only need to find how many prefixes and% k are the same. We use cnt to record the number of prefixes and% K. for example, if prefix and% k = 1, then cnt[1] + +.

Note that here, our i is calculated from the subscript of 0, and the prefix [0] is meaningless, or = 0, so cnt[0] is pre assigned = 1, which means there is already a case of = 0.

import java.util.Arrays;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int k = scan.nextInt();
		int[] num = new int[n];
		// Prefix and
		long[] preSum = new long[n + 1];
		for (int i = 0; i < n; i++) {
			num[i] = scan.nextInt();
			preSum[i + 1] = preSum[i] + num[i];
		}
		long[] cnt = new long[n + 1];
		// Here, you must initialize to 1, or modify the following for loop i subscript = 0
		cnt[0] = 1;
		long ans = 0;
		for (int i = 1; i < n + 1; i++) {
			ans += cnt[(int)(preSum[i] % k)];
			cnt[(int)(preSum[i] % k)]++;
		}
		System.out.println(ans);
	}
}

For the following content, please see the third and Fourth Lecture blog~