1, Arrays and strings

1. Find the central index of the array

Please calculate the central subscript of the array  

The central subscript of the array is a subscript of the array. The sum of all elements on the left is equal to the sum of all elements on the right.

If the central subscript is at the leftmost end of the array, the sum of the numbers on the left is regarded as 0 because there is no element to the left of the subscript. The same applies when the central subscript is at the right most end of the array.

If the array has multiple central subscripts, the one closest to the left should be returned. Returns - 1 if the array does not have a central subscript.

The complete code is as follows: (prefix and equal to suffix and)

​
#include<iostream>
#include<vector>
#include<numeric>
using namespace std;

class Solution {
public:
    int pivotindex(vector <int>& nums) {
        if (nums.empty())
        {
            return -1;
        }
        int left_sum = 0, right_sum = accumulate(nums.begin(), nums.end(), 0); //Cumulative summation
        for (int i = 0; i < nums.size(); i++)
        {
            left_sum += nums[i];
            if (i > 0)
            {
              right_sum -= nums[i-1];
            } 
            if (left_sum == right_sum)
            {
                cout << i << endl;
                return i;
            }
        }
        return -1;
        
    }

    void define(vector <int> &b, vector <int>::iterator& Iter1)
    {
        int d;
        cout << "Please enter the number of numbers:" << endl;
        scanf_s("%d", &d);
        cout << "please enter a number:" << endl;
        for (int i = 0; i < d; i++)   //Initialization of container
        {
            int a;
            scanf_s("%d",&a);
            b.push_back(a);
        }
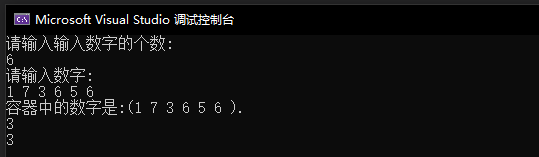
        cout << "The number in the container is:(";     //Traversal of numbers in containers
        for (Iter1 = b.begin(); Iter1 != b.end(); Iter1++)
        {
            cout << *Iter1 << " ";
        }
        cout << ")." << endl;
    }
};

int main()
{
    Solution a;
    vector <int> c;
    vector <int>::iterator it;
    a.define(c,it);
    cout << a.pivotindex(c) << endl;;
    return 0;
}

​

The operation results are as follows:

2. Search insertion location

Given a sort array and a target value, find the target value in the array and return its index. If the target value does not exist in the array, returns the position where it will be inserted in order.

You must use an algorithm with a time complexity of O(log n).

The code is as follows: (traversal, dichotomy)

​
​
​
//ergodic

class Solution
{
public:
    int searchInsert(vector<int>& a, int target)
    {
        for (int i = 0; i < a.size(); i++)
        {
           if(target<=a[i])
           {
              return i;
           }
        }
        return a.size();
    }
};


​//dichotomy

class Solution
{
public:
    int searchInsert(vector<int>& a, int target)
    {
        int left = 0, right = (a.size() - 1);
        while (left < right)
        {
            int mid = left + (right - left) / 2;
            if (a[mid]==target)
            {
                return mid;
            }
            else if (a[mid]>target)
            {
                right = mid - 1;

            }
            else if (a[mid] <target)
            {
                left = mid + 1;;

            }
        }            //After searching, left=right=mid
        return a[left] < target ? left + 1 : left;
    }
}

​

​

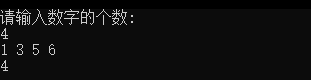
Operation results:

3. Merge interval

The set of several intervals is represented by an array of intervals, in which a single interval is intervals[i] = [starti, endi]. Please merge all overlapping intervals and return a non overlapping interval array, which needs to cover all the intervals in the input.

The complete code is as follows:

#include<iostream>
#include<vector>
#Include < algorithm > / / sort function header file
using namespace std;

class Solution
{
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) //The return value is a two-dimensional array type
    {
        int n = intervals.size();
        if (n == 1)
            return intervals;
        sort(intervals.begin(), intervals.end());   //First become an ordered array
        vector<vector<int>> vec;
        vec.push_back(intervals[0]);
        int j = 0;
        for (int i = j + 1; i < n; i++) {//If the last number of the previous array is greater than the first number of the subsequent array, there is an intersection
            if (intervals[i][0] <= vec[j][1])
                vec[j][1] = max(vec[j][1], intervals[i][1]);//The last number of the previous array is assigned the maximum value of the array
            else {
                vec.push_back(intervals[i]);  //Normal assignment
                j++;
            }
        }
        return vec;
    }
    void print(vector<vector<int>>& cd)    //Subscript printing two-dimensional array
    {

        for (int i = 0; i < cd.size(); i++)  //Number of containers
        {
            for (int j = 0; j < cd[i].size(); j++)  //Values in each container
            {
                cout << cd[i][j] <<" ";
            }
            cout << endl;
        }
    }
};

int main()
{
    Solution ab;
    vector<vector<int>> c = {         //Direct assignment
        {1,3},{2,6},{8,10},{15,18}
    };
    vector<vector<int> > d;
    d = ab.merge(c);
    ab.print(d);
    return 0;
}

Operation results:

4. Rotation matrix

Here's a picture by n × N matrix represents the image, where the size of each pixel is 4 bytes. Please design an algorithm to rotate the image 90 degrees. Can you do it without taking up additional memory space?

Topic analysis:

    Diagonal rotation: (blue indicates step)

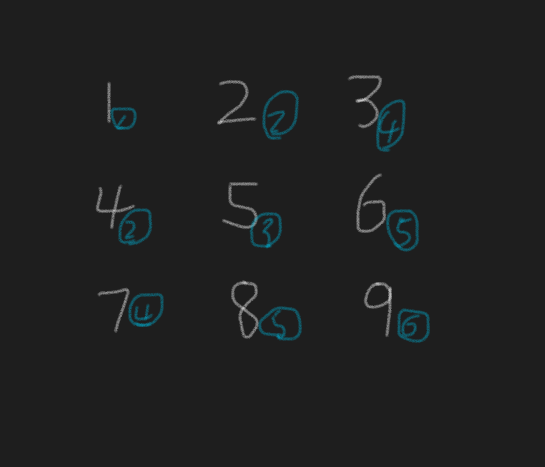
  The code is as follows:

​
class Solution
{
public:
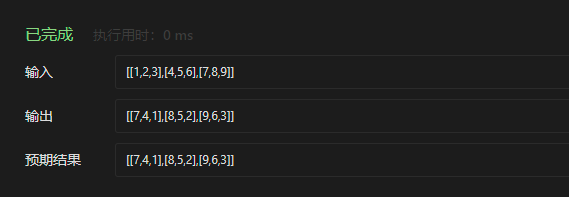
    vector<vector<int>> rorate(vector<vector<int>>& a)
    {
        int n;
        n = a.size();
       //Diagonal rotation
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < i; j++)   //See the figure below for details
            {
                swap(a[i][j], a[j][i]);
            }
        }
       //Mirror rotation
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n/2; j++)
            {
                swap(a[i][j], a[i][n - j - 1]);
            }
        }
        /*for (int i = 0; i < n; i++)        //reverse The function will reverse all the functions in the (begin, end) interval
        {
              reverse(a[i].begin(), a[i].end());   //The function is in the < algorithm > header file
        }*/     
        return a;
    }
}

​

Operation results:

  5, Zero matrix

Write an algorithm if M × If an element in N matrix is 0, its row and column are cleared.

  The code is as follows:

6, Diagonal traversal

Given a matrix with M x N elements (M rows, N columns), please return all elements in the matrix in diagonal traversal order.

analysis:

    Since the x+y (num) values of each diagonal are equal

    The rule is: if num is an even number, x=num;   If num is an odd number, y=num

    When the x value or y value is out of bounds, let x = the number of rows minus one, and y = the number of columns minus one

The code is as follows:

class Solution {
public:
   
    vector<int> findDiagonalOrder(vector<vector<int>>& matrix) {
        vector<int> ans;
        if(matrix.empty())
            return ans;
        int row = matrix.size(), col = matrix[0].size(), c = 0, r = 0;
        for(int i=0;i < row+col-1;i++)   //Diagonal x+y values must be the same
        {
            if(i % 2)  //When the diagonal value is odd
            {
                c = (i<col) ? i : col-1;  //When the sum is less than the number of rows (upper left triangular matrix), i=col, otherwise i=col-1 (cannot exceed the boundary)
                r = i - c;
                while(c >= 0 && r < row)
                    ans.push_back(matrix[r++][c--]);
            }
            else     //When the diagonal value is odd
            {
                r = (i<row) ? i : row-1;
                c = i - r;
                while(c < col && r >= 0)
                    ans.push_back(matrix[r--][c++]);
            }
        }
        return ans;
        
    }
};

Operation results:

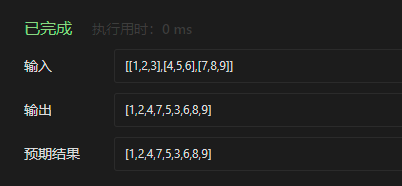
class Solution {
public:
    vector<int> findDiagonalOrder(vector<vector<int>>& matrix) {
        vector<int> ans;
        if(matrix.empty())
            return ans;
        int row = matrix.size(), col = matrix[0].size(), c = 0, r = 0;
        for(int i=0;i < row+col-1;i++)
        {
            if(i % 2)
            {
                c = (i<col) ? i : col-1;
                r = i - c;
                while(c >= 0 && r < row)
                    ans.push_back(matrix[r++][c--]);
            }
            else
            {
                r = (i<row) ? i : row-1;
                c = i - r;
                while(c < col && r >= 0)
                    ans.push_back(matrix[r--][c++]);
            }
        }
        return ans;
        
    }
};