Title Description

A path is defined as a sequence that starts from any node in the tree and connects along the parent node to the child node to reach any node. The same node can appear at most in a path sequence. Therefore, the path contains at least one node and does not necessarily pass through the root node.

Path sum is the sum of the values of each node in the path.
Give you the root node of a binary tree, root, and return its maximum path and.
Example 1:

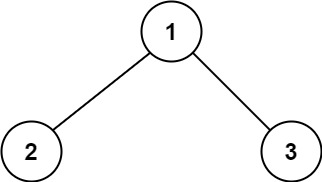
Input: root = [1, 2, 3]
Output: 6
 Explanation: the optimal path is 2->1->3，Path and are 2+1+3=6

Example 2

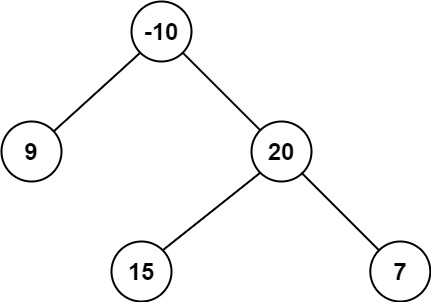
Input: root = [-10,9,20,null,null,15,7]
Output: 42
 Explanation: the optimal path is 15->20->7，Paths and are 15+20+7=42

Tips

• The range of nodes in the tree is [ 1 , 3 ∗ 1 0 4 ] [1, 3*10^4] [1,3∗104]
• − 1000 ≤ N o d e . v a l ≤ 1000 -1000 \le Node.val \le 1000 −1000≤Node.val≤1000

Problem solving process

This problem is solved by the idea of recursion. Firstly, the implementation defines a function maxGain, which is used to calculate the maximum contribution value of a node in the binary tree, that is, to find a path with the node as the starting point in the subtree with the node as the root node, so as to maximize the sum of node values on the path. The process is as follows:

• If the node is empty, the contribution value is 0;
• If the node is not empty, the contribution value is equal to the sum of the node value and the maximum contribution value in its child nodes (for leaf nodes, the maximum contribution value is its own value).

For example, consider the following binary tree:

   -10
   / \
  9  20
    /  \
   15   7

Among them, the maximum contribution values of leaf nodes 9, 15 and 7 are 9, 15 and 7 respectively. After the maximum contribution value of leaf nodes, the maximum contribution value of non leaf nodes is calculated. For example, the maximum contribution value of node 20 is 20+max(15,7)=35, and the maximum contribution value of node - 10 is - 10+max(9,35) = 25.

The above process is recursive. Therefore, call maxGain on the root node to calculate the maximum contribution value of each node.

After getting the maximum contribution value of each node, how to get the maximum path sum of the binary tree? For a node in a binary tree, the maximum path sum of the node depends on the value of the node and the maximum contribution value of the left and right child nodes of the node.

• If the maximum contribution value of the child node is positive, it is included in the maximum path sum of the node;
• If it is negative or 0, the maximum path sum of the node is not included.

Maintain a global variable maxSum, store the maximum path sum, and update the value of maxSum in the recursive process. Finally, the value of maxSum is the maximum path sum in the binary tree.

Code display

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# @FileName  :MaxPathSum.py
# @Time      :2022/1/24 19:39
# @Author    :PangXZ
from typing import Optional


# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def __init__(self):
        self.maxSum = float('-inf')

    def maxPathSum(self, root: TreeNode) -> int:
        def maxGain(node):
            if not node:
                return 0
            # Recursively calculate the maximum contribution value of the left and right child nodes
            # Only when the maximum contribution value is greater than 0 will the corresponding child node be selected
            leftGain = max(maxGain(node.left), 0)    # If the subtree path is negative, it should be set to 0, indicating that the maximum path does not contain the subtree
            rightGain = max(maxGain(node.right), 0)

            # The maximum path sum of the node depends on the value of the node and the maximum contribution value of the left and right child nodes of the node
            priceNewpath = node.val + leftGain + rightGain
            # Update the answer and judge whether the path sum of the left and right subtrees in the node is greater than the current maximum path sum
            self.maxSum = max(self.maxSum, priceNewpath)
            # Returns the maximum contribution value of the node
            return node.val + max(leftGain, rightGain)
        """
        For any node, if the maximum sum path contains the node, there are only two cases:
        1. The one with the larger path value formed by the left and right subtrees, plus the value of the node, traces back to the parent node to form the maximum path
        2. Both the left and right subtrees are in the maximum path, and the value of this node constitutes the final maximum path
        """
        maxGain(root)
        return self.maxSum

Complexity analysis

• Time complexity: O ( N ) O(N) O(N), where N is the number of nodes in the binary tree. No more than 2 visits to each node;
• Space complexity: O ( N ) O(N) O(N), the spatial complexity mainly depends on the number of recursive call layers. The maximum number of layers is equal to the height of the binary tree. In the worst case, the height of the binary tree is equal to the number of nodes in the binary tree.

Supplement: Java code

class Solution {
    int maxSum = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        maxGain(root);
        return maxSum;
    }
    public int maxGain(TreeNode node) {
        if (node == null) {
            return 0;
        }
        // Recursively calculate the maximum contribution value of the left and right child nodes
        // Only when the maximum contribution value is greater than 0 will the corresponding child node be selected
        int leftGain = Math.max(maxGain(node.left), 0);
        int rightGain = Math.max(maxGain(node.right), 0);

        // The maximum path sum of the node depends on the value of the node and the maximum contribution value of the left and right child nodes of the node
        int priceNewpath = node.val + leftGain + rightGain;

        // Update answer
        maxSum = Math.max(maxSum, priceNewpath);

        // Returns the maximum contribution value of the node
        return node.val + Math.max(leftGain, rightGain);
    }
}