Topic source

149. Maximum number of points on a line

Title details

Give you an array of points, where points[i] = [xi, yi] represents a point on the X-Y plane. Find the maximum number of points on the same line.

Example 1:

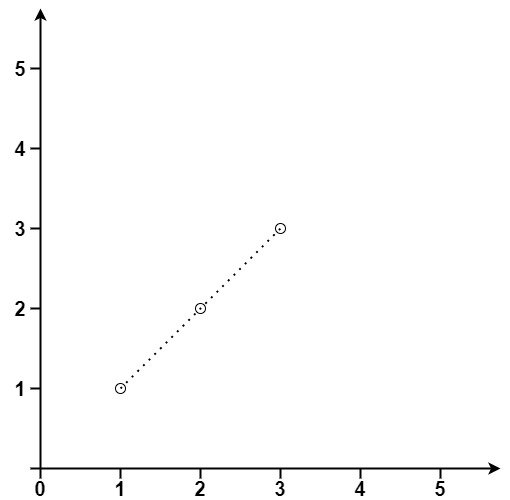
Input: points = [[1,1],[2,2],[3,3]]
Output: 3

Example 2:

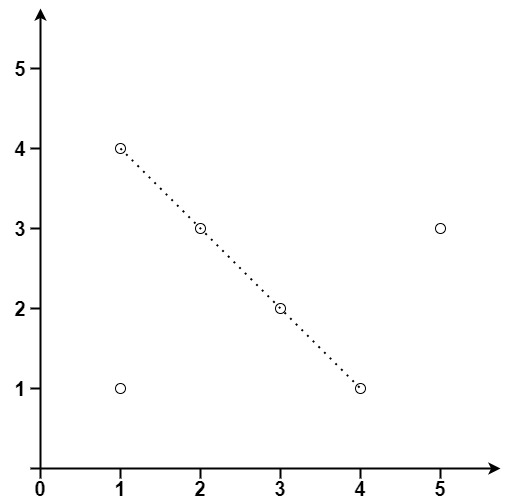
Input: points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
Output: 4

Tips:

• 1 <= points.length <= 300
• points[i].length == 2
• -104 <= xi, yi <= 104
• All points in points are different from each other

Problem solving analysis

Solution 1: Violence Law

class Solution {
    public int maxPoints(int[][] points) {
        int n = points.length;
        // y1 = kx1 + b
        // y2 = kx2 + b
        // k = (y1-y2) / (x1-x2), b = y1 - x1 * ((y1-y2) / (x1-x2))
        
        int ans = 1;
        for(int i=0; i<n; i++){
            int x1 = points[i][0], y1= points[i][1];
            for(int j=i+1; j<n; j++){
                int x2 = points[j][0], y2= points[j][1];
                int max = 2;
                for(int k=j+1; k<n; k++){
                    int x3 = points[k][0], y3= points[k][1];
                    // Instead of directly comparing the two slopes, the comparison of division is converted into Multiplication comparison
                    int temp1 = (y2-y1) * (x3-x2);
                    int temp2 = (y3-y2) * (x2-x1);
                    if(temp1 == temp2){
                        max++;
                    }
                }
                ans = Math.max(ans, max);
            }
        }
        return ans;
    }
}

Solution 2: HashMap optimization

1. From solution 1, we can see that the time complexity of this method is \ (O(n^3) \), so what method can reduce the time complexity?
2. For this question, we can think from how to judge that two points are collinear. In method 1, we judge whether it is collinear with the existing straight line by traversing all the remaining points. From here, we can see that we only need to fix the starting point, then traverse the remaining points, and then record the slope between them and the starting point. If the slope is the same, it indicates that these points must be collinear (there is no need to judge the intercept, because the starting point is fixed, which is equivalent to the fixed intercept).
3. Therefore, here we can use a HashMap to store the slope, and summarize all points with the same slope in the inner layer cycle. The line with the most points is the best line starting from the starting point.
4. In addition, there is another problem in this problem, that is, it is possible that the slope we calculate is double. If we store it directly as a key, we may face the problem of loss of accuracy. What should we store? Starting from the formula for calculating the slope, k=(y1-y2)/(x1-x2), we can store y1-y2 and x1-x2, which can determine the slope. However, we cannot directly store y1-y2 and x1-x2, because there can be a multiple relationship between them, so we need to divide y1-y2 and x1-x2 completely.

class Solution {
    public int maxPoints(int[][] points) {
        int n = points.length;
        // y1 = kx1 + b
        // y2 = kx2 + b
        // k = (y1-y2) / (x1-x2), b = y1 - x1 * ((y1-y2) / (x1-x2))
        
        int ans = 0;
        for(int i=0; i<n; i++){
            int x1 = points[i][0], y1= points[i][1];
            Map<String,Integer> map = new HashMap<>();
            int max = 0;
            for(int j=i+1; j<n; j++){
                int x2 = points[j][0], y2= points[j][1];
                int ydif = y1-y2;
                int xdif = x1-x2;
                int common = gcd(ydif, xdif);
                String key = Arrays.toString(new int[]{ydif/common, xdif/common});
                int num = map.getOrDefault(key, 0);
                map.put(key, num + 1);
                max = Math.max(max, num+1);
            }
            ans = Math.max(ans , max +1);
        }
        return ans;
    }

    private int gcd(int a, int b){
        return b == 0 ? a : gcd(b, a%b);
    }
}