Title Description:
Given an array of size n, find most of its elements. Most elements refer to elements that appear more than ⌊ n/2 ⌋ in the array.
You can assume that the array is non empty and that there are always many elements in a given array.
Example
1: Input: [3,2,3]
Output: 3
2: Input: [2,2,1,1,1,2,2]
Output: 2
Idea:

1. Violent solution: double-layer loop, enumerate each element, traverse to get the number of each element, and then find the one with the largest number of elements. The time complexity is O(n^2).
2. Using the hash table map, the key value pair is (key,count), count the number of occurrences of each element, and then traverse the map to get the element with the most occurrences. The time complexity is O(n) and the space complexity is O(n).

class Solution(object):
    def majorityElement(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        dict = {}
        max = 0
        for i in range(len(nums)):
            if nums[i] in dict.keys():
                dict[nums[i]] += 1
            else:
                dict[nums[i]] = 1
        for key, value in dict.items():
            if value > max:
                val = key
                max = value
        return val

1. sort the entire array. Because most elements appear more than n/2, the element with the subscript | n/2 | is the desired element. The time complexity is O(n logn), the space complexity of self writing heap can be O(1), and the space complexity of Library debugging is O(logn).
2. Divide and Conquer:
   If the number a is the mode of the array num, if we divide num into two parts, then a must be at least part of the mode. Divide the array into left and right parts, calculate the mode a1 of the left half and the mode a2 of the right half respectively, and then select the correct mode from a1 and a2.
   The divide and conquer algorithm is used to solve recursively until all subproblems are arrays of length 1. The only number in the subarray with length 1 is obviously the mode, which can be returned directly. If the length of an interval after backtracking is greater than 1, we must merge the values of the left and right sub intervals. If they have the same mode, it is obvious that the mode of this interval is their same value. Otherwise, we need to compare the number of times two modes appear in the whole interval to determine the mode of the interval, that is, traversal.

class Solution(object):
    def majorityElement(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        return self.majorty(nums, 0, len(nums)-1)

    def majorty(self, nums, start, end):
        if start == end:
            return nums[start]
        else:
            mid = int((start + end) / 2)
            left = self.majorty(nums, start, mid)
            right = self.majorty(nums, mid+1, end)
            if left == right:
                return left
            else:
                count_left = 0
                count_right = 0
                for i in range(end-start+1):
                    if nums[start+i] == left:
                        count_left += 1
                    elif nums[start+i] == right:
                        count_right += 1
                if count_left >= count_right:
                    return left
                else:
                    return right

Complexity analysis

Time complexity: O(nlogn). The function majority() will solve two subproblems with a length of n/2 and do two linear scans with a length of n (the last whole traversal). Therefore, the time complexity of the divide and conquer algorithm can be expressed as:
T(n) = 2T(n/2) + 2n
According to the main theorem, this problem satisfies the second case, so the time complexity can be expressed as:

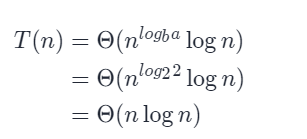
Main theorem:

Spatial complexity: O(logn). Although the divide and conquer algorithm does not directly allocate additional array space, it uses additional stack space in the process of recursion. The algorithm divides the array into two parts from the middle each time, so O(logn) recursion is required before the array length becomes 1, that is, the space complexity is O(logn).

1. Moore voting method: Boyer Moore voting algorithm
   Because the number of occurrences of the required number is greater than n/2, the idea of pairwise confrontation and cancellation is adopted to traverse the array. Specifically, set a winner and count it, so that the first element of the array is winner, and no different values offset each other, count-=1; If the offset is gone, the next value of the array is taken as winner; If you encounter the same number as winner, count+=1. Finally, winner is what you want, because his number is greater than n/2 and will never be offset.

class Solution(object):
    def majorityElement(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        winner = None
        count = 0
        for i in range(len(nums)):
            if count == 0:
                winner = nums[i]
            if nums[i] != winner:
                count -= 1
            elif nums[i] == winner:
                count += 1
        return winner

The time complexity is O(n), and the space complexity is O(1).